人教版八年级数学上册 13.1 .1 轴对称学案 (word版 无答案)
文档属性
| 名称 | 人教版八年级数学上册 13.1 .1 轴对称学案 (word版 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 17:31:42 | ||
图片预览

文档简介
第1课时
13.1
.1
轴对称
班别
姓名
学号
学习目标:
1.认识轴对称图形,并能准确地找出他的对称轴;
2.会判定一个图形是不是轴对称图形;
3.会区别轴对称图形和两个图形成轴对称;
二、学习探究:
1、阅读教材P58-60,完成预习内容:
1.如果一个平面图形沿一条______折叠,______两旁的部分能够
,这个图形就叫做轴对称图形,这条______就是它的对称轴,这时,我们也说这个图形关于这条_______(成轴)
对称。
2.一个图形沿着某一条直线折叠,如果它能够与
重合,那么就说
关于这条直线(成轴)对称,这条直线叫做__________,折叠后
叫做对称点。
3.参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
4.如图,两幅图关于直线l轴对称,请在图形中标出点A、B和C关于直线l的轴对称点.
第4题
第5题
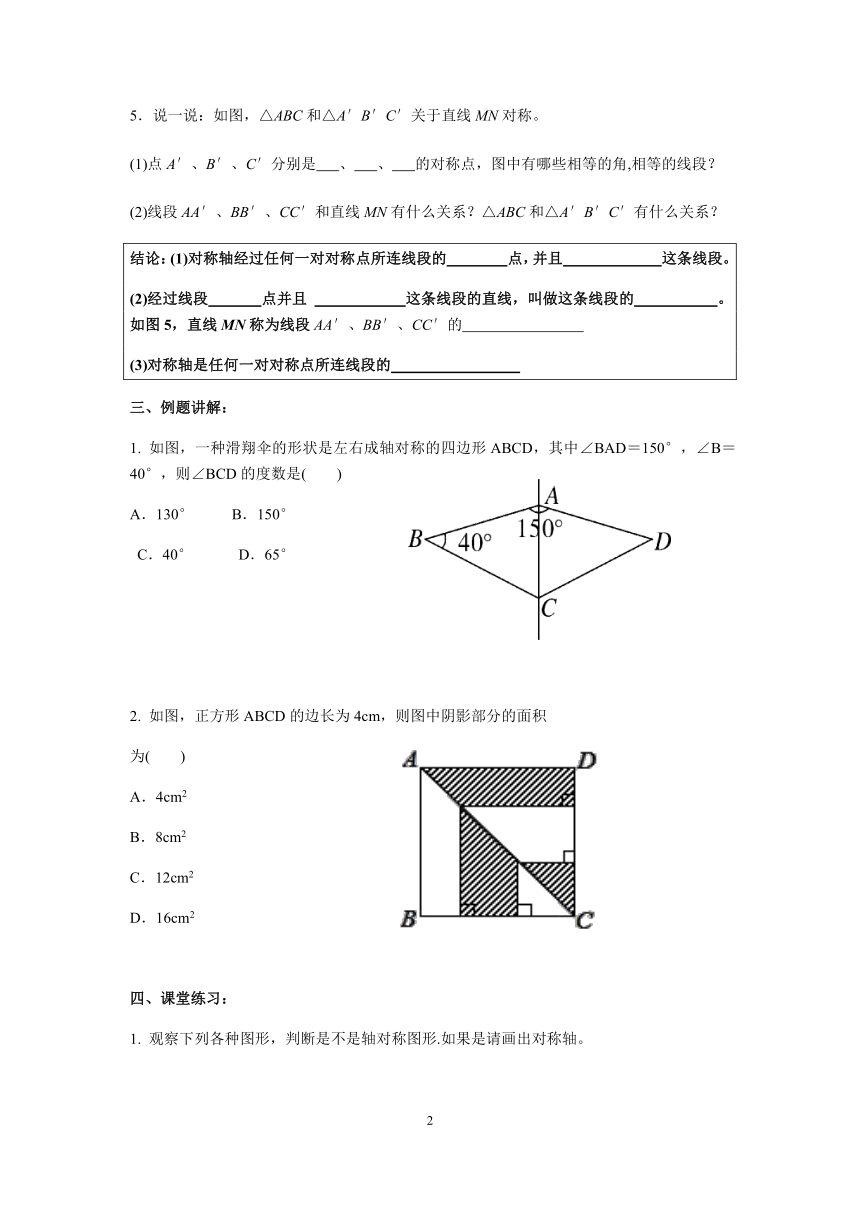
5.说一说:如图,△ABC和△A′B′C′关于直线MN对称。
(1)点A′、B′、C′分别是
、
、
的对称点,图中有哪些相等的角,相等的线段?
(2)线段AA′、BB′、CC′和直线MN有什么关系?△ABC和△A′B′C′有什么关系?
结论:(1)对称轴经过任何一对对称点所连线段的
点,并且
这条线段。
(2)经过线段
点并且
这条线段的直线,叫做这条线段的
。如图5,直线MN称为线段AA′、BB′、CC′的
(3)对称轴是任何一对对称点所连线段的
三、例题讲解:
1.
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130°
B.150°
C.40°
D.65°
2.
如图,正方形ABCD的边长为4cm,则图中阴影部分的面积
为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
四、课堂练习:
1.
观察下列各种图形,判断是不是轴对称图形.如果是请画出对称轴。
2.下面图形中,哪些是轴对称图形,哪些不是轴对称图形?如果是请画出对称轴。
3.
下列每幅图形都是轴对称图形,请画出它们的对称轴,它们的对称轴唯一吗?
4.如图所示的每幅图形中的两个图案是轴对称的吗?如果是,指出它们的对称轴,并找出一对对称点。
五、作业
(A组)
1.
如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
2.
找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
(B组)
3.下列说法正确的是(
).
(A)若两个三角形全等,则它们必关于某条直线成轴对称
(B)直角三角形是关于斜边上的中线成轴对称的图形
(C)如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
(D)线段是关于经过该线段中点的直线成轴对称的图形
4.
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_______.
(C组)
5.下图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中
所示的方向被击出(球可以经过多次反射),那么该球最后
将落入的球袋是
(
)
A.
1号袋
B.
2号袋
C.
3号袋
D.
4号袋
13.1
.1
轴对称
班别
姓名
学号
学习目标:
1.认识轴对称图形,并能准确地找出他的对称轴;
2.会判定一个图形是不是轴对称图形;
3.会区别轴对称图形和两个图形成轴对称;
二、学习探究:
1、阅读教材P58-60,完成预习内容:
1.如果一个平面图形沿一条______折叠,______两旁的部分能够
,这个图形就叫做轴对称图形,这条______就是它的对称轴,这时,我们也说这个图形关于这条_______(成轴)
对称。
2.一个图形沿着某一条直线折叠,如果它能够与
重合,那么就说
关于这条直线(成轴)对称,这条直线叫做__________,折叠后
叫做对称点。
3.参照下图说明轴对称图形与两个图形成轴对称有什么区别与联系?
4.如图,两幅图关于直线l轴对称,请在图形中标出点A、B和C关于直线l的轴对称点.
第4题
第5题
5.说一说:如图,△ABC和△A′B′C′关于直线MN对称。
(1)点A′、B′、C′分别是
、
、
的对称点,图中有哪些相等的角,相等的线段?
(2)线段AA′、BB′、CC′和直线MN有什么关系?△ABC和△A′B′C′有什么关系?
结论:(1)对称轴经过任何一对对称点所连线段的
点,并且
这条线段。
(2)经过线段
点并且
这条线段的直线,叫做这条线段的
。如图5,直线MN称为线段AA′、BB′、CC′的
(3)对称轴是任何一对对称点所连线段的
三、例题讲解:
1.
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130°
B.150°
C.40°
D.65°
2.
如图,正方形ABCD的边长为4cm,则图中阴影部分的面积
为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
四、课堂练习:
1.
观察下列各种图形,判断是不是轴对称图形.如果是请画出对称轴。
2.下面图形中,哪些是轴对称图形,哪些不是轴对称图形?如果是请画出对称轴。
3.
下列每幅图形都是轴对称图形,请画出它们的对称轴,它们的对称轴唯一吗?
4.如图所示的每幅图形中的两个图案是轴对称的吗?如果是,指出它们的对称轴,并找出一对对称点。
五、作业
(A组)
1.
如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
2.
找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
(B组)
3.下列说法正确的是(
).
(A)若两个三角形全等,则它们必关于某条直线成轴对称
(B)直角三角形是关于斜边上的中线成轴对称的图形
(C)如果两个三角形关于某条直线成轴对称,那么它们是全等三角形
(D)线段是关于经过该线段中点的直线成轴对称的图形
4.
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_______.
(C组)
5.下图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中
所示的方向被击出(球可以经过多次反射),那么该球最后
将落入的球袋是
(
)
A.
1号袋
B.
2号袋
C.
3号袋
D.
4号袋
