苏科版八年级上册 第六章 一次函数应用(图像综合)解答题题拔高训练(一)(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册 第六章 一次函数应用(图像综合)解答题题拔高训练(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 83.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 10:12:13 | ||
图片预览




文档简介
第六章
一次函数应用(图像综合)
解答题题拔高训练(一)
1.某电话公司开设了两种手机通讯业务,甲种业务:使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;乙种业务:不交月租费,每通话1分钟,付话费0.6元(指市话).若一个月内通话x分钟,两种方式的费用分别为y1(元)和y2(元).
(1)分别求出y1、y2与x之间的函数关系式.
(2)根据每月可能的通话时间,作为消费者选用哪种缴费方式更实惠.
2.某超市销售10套A品牌运动装和20套B品牌的运动装的利润为4000元,销售20套A品牌和10套B品牌的运动装的利润为3500元.
(1)该商店计划一次购进两种品牌的运动装共100套,设超市购进A品牌运动装x套,这100套运动装的销售总利润为y元,求y关于x的函数关系式;
(2)在(1)的条件下,若B品牌运动装的进货量不超过A品牌的2倍,该商店购进A、B两种品牌运动服各多少件,才能使销售总利润最大?
(3)实际进货时,厂家对A品牌运动装出厂价下调,且限定超市最多购进A品牌运动装70套,A品牌运动装的进价降低了m(0<m<100)元,若商店保持两种运动装的售价不变,请你根据以上信息及(2)中的条件,设计出使这100套运动服销售总利润最大的进货方案.
3.某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园
游客进园需购买20元/人的门票,采摘的樱桃六折优惠
乙园
游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为x(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为y1(元)在乙采摘园所需总费用为y2(元),图中的折线OAB表示y2与x之间的函数关系.
(1)①甲、乙两果园的樱桃单价为
元/千克;
②直接写出y1的函数表达式:
,并在图中补画出y1的函数图象;
(2)求出y2与x之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于30千克,选择哪个采摘园更划算?请说明理由.
4.预防新型冠状病毒期间,某种消毒液广宁需要6吨,怀柔需要8吨,正好端州储备有10吨,四会储备有4吨,市预防新型冠状病毒领导小组决定将这14吨消毒液调往广宁和怀柔,消毒液的运费价格如下表(单位:元/吨)设从端州调运x吨到广宁.
起点\终点
广宁
怀柔
端州
60
100
四会
35
70
(1)求调运14吨消毒液的总运费y关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费的多少?
5.一水果生态园种植有黑叶荔和妃子笑两种荔枝,某天安排50名工人采摘荔枝(每名工人只采摘一个品种的荔枝),且每人每天只能摘0.4吨黑叶荔或0.36吨妃子笑,若当天的黑叶荔售价每吨4000元,妃子笑售价每吨5000元,设安排其中x名工人采摘黑叶荔,两种荔枝当天全部售出,销售总额达y元.
(1)求y随x变化的解析式,并指出自变量x的取值范围;
(2)若要求当天采摘的黑叶荔数量不少于的妃子笑数量,求销售总额y的最大值.
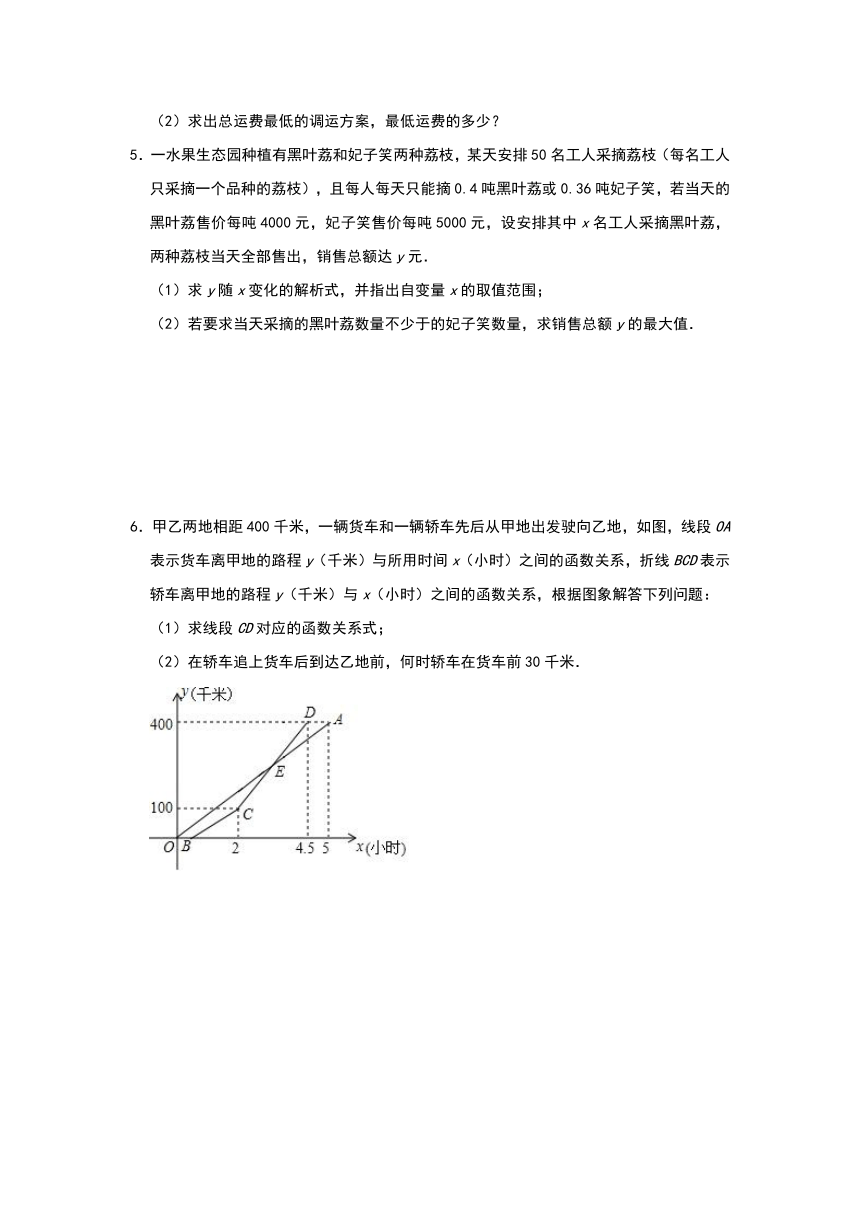
6.甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段CD对应的函数关系式;
(2)在轿车追上货车后到达乙地前,何时轿车在货车前30千米.
7.某市为了鼓励居民在枯水期(当年11月至第二年5月)节约用电,规定7:00至23:00为用电高峰期,此期间用电电费y1(单位:元)与用电量x(单位:度)之间满足的关系如图1所示;规定23:00至第二天早上7:00为用电低谷期,此期间用电电费y2(单位:元)与用电量x(单位:元)之间满足如表1所示的一次函数关系.
(1)求y2与x的函数关系式;并直接写出当0≤x≤180和x>180时,y1与x的函数关系式;
(2)若市民王先生一家在12月份共用电350度,支付电费150元,求王先生一家在高峰期和低谷期各用电多少度.
低谷期用电量x度
…
80
100
140
…
低谷期用电电费y2元
…
20
25
35
…
8.抗击新冠疫情期间,一方危急,八方支援.当吉林市疫情严重时,急需大量医疗防护物资.现知A城有医疗防护物资200t,B城有医疗防护物资300t.现要把这些医疗物资全部运往C、D两市.从A城往C、D两市的运费分别为20元/t和25元/t;从B城往C、D两市的运费分别为15元/t和24元/t.现C市需要物资240t,D市需要物资260t.若设从A城往C市运xt.请回答下列问题:
(1)用含x的式子表示从A往D市运物资的数量为t,从B往C市运物资的数量为t,从B往D市运物资的数量为t(写化简后的式子).
(2)求出怎样调运物资可使总运费最少?最少运费是多少?
9.快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程
km;快车的速度为
km/h;慢车的速度为
km/h;
(2)出发
小时后,快慢两车相遇;
(3)求快慢两车出发几小时后第一次相距150km?
10.图书馆与学校相距600m,明明从学校出发步行去图书馆,亮亮从图书馆骑车去学校两人同时出发,匀速相向而行,他们与学校的距离S(m)与时间t(s)的图象如图所示:
根据图象回答:
(1)明明步行的速度为
m/s;亮亮骑车的速度为
m/s.
(2)分别写出明明、亮亮与学校的距离S1、S2与时间t的关系式.
(3)通过计算求出a的值.
参考答案
1.解:(1)由题意可知:y1=50+0.4x,y2=0.6x;
(2)y1=50+0.4x,y2=0.6x,
当y1>y2即50+0.4x>0.6x时,x<250,
当y1=y2即50+0.4x=0.6x时,x=250,
当y1<y2即50+0.4x<0.6x时,x>250,
所以,当通话时间小于250分钟时,选择乙种通信业务更优惠,
当通话时间等于250分钟时,选择两种通信业务一样,
当通话时间大于250分钟时,选择甲种通信业务更优惠.
2.解:(1)设每套A种品牌的运动装的销售利润为a,每套B品牌的运动装的销售利润为b元.
得,解得:,
所以y=100x+150(100﹣x),即y=﹣50x+15000
(2)根据题意得:100﹣x≤2x,解得:x≥33,
∵y=﹣50x+15000,﹣50<0,
∴y随x的增大而减小.
∵x为正整数,
∴当x=34时,y取得最大值,此时100﹣x=66,即超市购进34套A品牌运动装和66套B品牌运动装才能获得最大利润;
(3)根据题意得:y=(100+m)x+150(100﹣x),即y=(m﹣50)x+15000,(33≤x≤70).
①当0<m<50时,m﹣50<0,y随x的增大而减小.
∴当x=34时,y取得最大值,超市购进34套A品牌运动装和66套B品牌运动装才能获得最大利润;
②当m=50时,m﹣50=0,y=15000,即超市购进A品牌的运动装数量满足33≤x≤70的证书是,均获得最大利润;
③当50<m<100时,m﹣50>0,y随x的增大而增大,
∴x=70时,y取得最大值,即超市购进70套A品牌运动装和30套B品牌运动装才能获得最大利润.
3.解:(1)①300÷10=30(元/千克);
故答案为:30;
②y1=30×0.6x+20×3=18x+60;y1的函数图象如图所示.
故答案为:y1=18x+60;
(2)由图可得,当0≤x≤10时,y2=30x,
当x>10时,设y2=kx+b.
将(10,300)和(20,450)代入y2=kx+b,
得,解得,
∴当x>10时,y2=15x+150.
∴;
(3)令y1<y2,即18x+60<15x+150,解得x<30;
令y1=y2,即18x+60=15x+150,解得x=30;
令y1>y2,即18x+60>15x+150,解得x>30.
答:当樱桃采摘量x=30千克时,两家采摘园所需费用相同;
当樱桃采摘量x的范围为x>30千克时,乙采摘园更划算.
4.解:(1)设从端州调运x吨到广宁,则从端州调运(10﹣x)吨到怀柔,从四会调运(6﹣x)吨到广宁,从四会调运8﹣(10﹣x)=(x﹣2)吨到怀柔,
依题意,得:y=60x+100(10﹣x)+35(6﹣x)+70(x﹣2)=﹣5x+1070.
(2)依题意,得:,
解得:2≤x≤6.
∵在一次函数y=﹣5x+1070中,k=﹣5<0,
∴y随x增大而减小,
∴当x=6时,y取得最小值,最小值=﹣5×6+1070=1040,
∴从端州调运6吨到广宁,从端州调运4吨到怀柔,从四会调运4吨到怀柔时,总运费最低,最低运费为1040元.
5.解:(1)设安排其中x名工人采摘黑叶荔,则按(50﹣x)名工人采摘妃子笑,
y=4000×0.4x+5000×0.36×(50﹣x)=﹣200x+90000,
即y与x的函数关系式为y=﹣200x+90000(0≤x≤50);
(2)∵当天采摘的黑叶荔数量不少于的妃子笑数量,
∴0.4x≥0.36×(50﹣x),
解得,x≥23,
∵y=﹣200x+90000,
∴y随x的增大而减小,
又∵x为整数,
∴当x=24时,y取得最大值,此时y=85200,
答:若要求当天采摘的黑叶荔数量不少于的妃子笑数量,销售总额的最大值是85200元.
6.解:(1)设线段CD对应的函数表达式为y=kx+b.
将C(2,100)、D(4.5,400)代入y=kx+b中,得
解方程组得
所以线段CD所对应的函数表达式为y=120x﹣140(2≤x≤4.5).
(2)根据题意得,120x﹣140﹣80x=30,解得.
答:当x=时,轿车在货车前30千米.
7.解:(1)设y2与x的函数关系式为y=k2x+b2,根据题意得,
解得,
∴y2与x的函数关系式为y2=0.25x;
当0≤x≤180时,y1与x的函数关系式为y=0.5x;
当x>180时,设y1=k1+b1,根据题意得
,
解得,
∴y1与x的函数关系式为y1=0.6x﹣18;
∴;
(2)设王先生一家在高峰期用电x度,低谷期用电y度,
当0≤x≤180时,,
解得,不合题意,舍去;
当x>180时,,
解得.
答:王先生一家在高峰期用电230度,低谷期用电120度.
8.解:(1)用含x的式子表示从A往D市运
(
200﹣x
)t,
从B往C市运
(240﹣x)t,
从B往
D市运
(60+x)t,
(2)设总运费为W元,则有
W=20x+25(
200﹣x
)+15(240﹣x)+24(60+x)
=4x+10040,
∵0≤x≤200,W随x的增大而增大,
∴当x=0时,W有最小值,
即从A往D调200t,从B往D调60t,从B往C调240t时,总运费最少为10040元.
9.解:(1)由函数图象可得,
甲乙两地之间的路程是560km,快车的速度为:560÷(5﹣1)=140(km/h),慢车的速度为:560÷(5+4﹣1)=70(km/h),
故答案为:140,70;
(2)设出发a小时时,快慢两车相遇,
140a+70a=560,
解得,a=,
即出发小时后,快慢两车相遇,
故答案为:;
(3)快慢两车出发b小时后第一次相距150km,
140b+70b=560﹣150,
解得,b=,
即快慢两车出发小时后第一次相距150km
10.解:(1)由图象可知:学校和图书馆之间的距离为600米,亮亮用200秒骑车从图书馆到学校,而明明用300秒从到图书馆,
因此亮亮速度为:600÷200=3米/秒,明明的速度为600÷300=2米/秒,
故答案为:2,3.
(2)设明明的S1与t的关系式为S1=k1t,把(300,600)代入得:k1=2
∴S1=2t,
设亮亮的S2与t的关系式为S2=k2t+b,把(0,600)(200,0)代入得:
,解得:k2=﹣3,b=600,
∴S2=﹣3t+600,
答:明明、亮亮与学校的距离S1、S2与时间t的关系式分别为S1=2t,S2=﹣3t+600.
(3)当S1=S2时,即2t=﹣3t+600,解得t=120,即a=120s.
答:a的值为120秒.
一次函数应用(图像综合)
解答题题拔高训练(一)
1.某电话公司开设了两种手机通讯业务,甲种业务:使用者先缴50元月租费,然后每通话1分钟,再付话费0.4元;乙种业务:不交月租费,每通话1分钟,付话费0.6元(指市话).若一个月内通话x分钟,两种方式的费用分别为y1(元)和y2(元).
(1)分别求出y1、y2与x之间的函数关系式.
(2)根据每月可能的通话时间,作为消费者选用哪种缴费方式更实惠.
2.某超市销售10套A品牌运动装和20套B品牌的运动装的利润为4000元,销售20套A品牌和10套B品牌的运动装的利润为3500元.
(1)该商店计划一次购进两种品牌的运动装共100套,设超市购进A品牌运动装x套,这100套运动装的销售总利润为y元,求y关于x的函数关系式;
(2)在(1)的条件下,若B品牌运动装的进货量不超过A品牌的2倍,该商店购进A、B两种品牌运动服各多少件,才能使销售总利润最大?
(3)实际进货时,厂家对A品牌运动装出厂价下调,且限定超市最多购进A品牌运动装70套,A品牌运动装的进价降低了m(0<m<100)元,若商店保持两种运动装的售价不变,请你根据以上信息及(2)中的条件,设计出使这100套运动服销售总利润最大的进货方案.
3.某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园
游客进园需购买20元/人的门票,采摘的樱桃六折优惠
乙园
游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为x(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为y1(元)在乙采摘园所需总费用为y2(元),图中的折线OAB表示y2与x之间的函数关系.
(1)①甲、乙两果园的樱桃单价为
元/千克;
②直接写出y1的函数表达式:
,并在图中补画出y1的函数图象;
(2)求出y2与x之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于30千克,选择哪个采摘园更划算?请说明理由.
4.预防新型冠状病毒期间,某种消毒液广宁需要6吨,怀柔需要8吨,正好端州储备有10吨,四会储备有4吨,市预防新型冠状病毒领导小组决定将这14吨消毒液调往广宁和怀柔,消毒液的运费价格如下表(单位:元/吨)设从端州调运x吨到广宁.
起点\终点
广宁
怀柔
端州
60
100
四会
35
70
(1)求调运14吨消毒液的总运费y关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费的多少?
5.一水果生态园种植有黑叶荔和妃子笑两种荔枝,某天安排50名工人采摘荔枝(每名工人只采摘一个品种的荔枝),且每人每天只能摘0.4吨黑叶荔或0.36吨妃子笑,若当天的黑叶荔售价每吨4000元,妃子笑售价每吨5000元,设安排其中x名工人采摘黑叶荔,两种荔枝当天全部售出,销售总额达y元.
(1)求y随x变化的解析式,并指出自变量x的取值范围;
(2)若要求当天采摘的黑叶荔数量不少于的妃子笑数量,求销售总额y的最大值.
6.甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
(1)求线段CD对应的函数关系式;
(2)在轿车追上货车后到达乙地前,何时轿车在货车前30千米.
7.某市为了鼓励居民在枯水期(当年11月至第二年5月)节约用电,规定7:00至23:00为用电高峰期,此期间用电电费y1(单位:元)与用电量x(单位:度)之间满足的关系如图1所示;规定23:00至第二天早上7:00为用电低谷期,此期间用电电费y2(单位:元)与用电量x(单位:元)之间满足如表1所示的一次函数关系.
(1)求y2与x的函数关系式;并直接写出当0≤x≤180和x>180时,y1与x的函数关系式;
(2)若市民王先生一家在12月份共用电350度,支付电费150元,求王先生一家在高峰期和低谷期各用电多少度.
低谷期用电量x度
…
80
100
140
…
低谷期用电电费y2元
…
20
25
35
…
8.抗击新冠疫情期间,一方危急,八方支援.当吉林市疫情严重时,急需大量医疗防护物资.现知A城有医疗防护物资200t,B城有医疗防护物资300t.现要把这些医疗物资全部运往C、D两市.从A城往C、D两市的运费分别为20元/t和25元/t;从B城往C、D两市的运费分别为15元/t和24元/t.现C市需要物资240t,D市需要物资260t.若设从A城往C市运xt.请回答下列问题:
(1)用含x的式子表示从A往D市运物资的数量为t,从B往C市运物资的数量为t,从B往D市运物资的数量为t(写化简后的式子).
(2)求出怎样调运物资可使总运费最少?最少运费是多少?
9.快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程
km;快车的速度为
km/h;慢车的速度为
km/h;
(2)出发
小时后,快慢两车相遇;
(3)求快慢两车出发几小时后第一次相距150km?
10.图书馆与学校相距600m,明明从学校出发步行去图书馆,亮亮从图书馆骑车去学校两人同时出发,匀速相向而行,他们与学校的距离S(m)与时间t(s)的图象如图所示:
根据图象回答:
(1)明明步行的速度为
m/s;亮亮骑车的速度为
m/s.
(2)分别写出明明、亮亮与学校的距离S1、S2与时间t的关系式.
(3)通过计算求出a的值.
参考答案
1.解:(1)由题意可知:y1=50+0.4x,y2=0.6x;
(2)y1=50+0.4x,y2=0.6x,
当y1>y2即50+0.4x>0.6x时,x<250,
当y1=y2即50+0.4x=0.6x时,x=250,
当y1<y2即50+0.4x<0.6x时,x>250,
所以,当通话时间小于250分钟时,选择乙种通信业务更优惠,
当通话时间等于250分钟时,选择两种通信业务一样,
当通话时间大于250分钟时,选择甲种通信业务更优惠.
2.解:(1)设每套A种品牌的运动装的销售利润为a,每套B品牌的运动装的销售利润为b元.
得,解得:,
所以y=100x+150(100﹣x),即y=﹣50x+15000
(2)根据题意得:100﹣x≤2x,解得:x≥33,
∵y=﹣50x+15000,﹣50<0,
∴y随x的增大而减小.
∵x为正整数,
∴当x=34时,y取得最大值,此时100﹣x=66,即超市购进34套A品牌运动装和66套B品牌运动装才能获得最大利润;
(3)根据题意得:y=(100+m)x+150(100﹣x),即y=(m﹣50)x+15000,(33≤x≤70).
①当0<m<50时,m﹣50<0,y随x的增大而减小.
∴当x=34时,y取得最大值,超市购进34套A品牌运动装和66套B品牌运动装才能获得最大利润;
②当m=50时,m﹣50=0,y=15000,即超市购进A品牌的运动装数量满足33≤x≤70的证书是,均获得最大利润;
③当50<m<100时,m﹣50>0,y随x的增大而增大,
∴x=70时,y取得最大值,即超市购进70套A品牌运动装和30套B品牌运动装才能获得最大利润.
3.解:(1)①300÷10=30(元/千克);
故答案为:30;
②y1=30×0.6x+20×3=18x+60;y1的函数图象如图所示.
故答案为:y1=18x+60;
(2)由图可得,当0≤x≤10时,y2=30x,
当x>10时,设y2=kx+b.
将(10,300)和(20,450)代入y2=kx+b,
得,解得,
∴当x>10时,y2=15x+150.
∴;
(3)令y1<y2,即18x+60<15x+150,解得x<30;
令y1=y2,即18x+60=15x+150,解得x=30;
令y1>y2,即18x+60>15x+150,解得x>30.
答:当樱桃采摘量x=30千克时,两家采摘园所需费用相同;
当樱桃采摘量x的范围为x>30千克时,乙采摘园更划算.
4.解:(1)设从端州调运x吨到广宁,则从端州调运(10﹣x)吨到怀柔,从四会调运(6﹣x)吨到广宁,从四会调运8﹣(10﹣x)=(x﹣2)吨到怀柔,
依题意,得:y=60x+100(10﹣x)+35(6﹣x)+70(x﹣2)=﹣5x+1070.
(2)依题意,得:,
解得:2≤x≤6.
∵在一次函数y=﹣5x+1070中,k=﹣5<0,
∴y随x增大而减小,
∴当x=6时,y取得最小值,最小值=﹣5×6+1070=1040,
∴从端州调运6吨到广宁,从端州调运4吨到怀柔,从四会调运4吨到怀柔时,总运费最低,最低运费为1040元.
5.解:(1)设安排其中x名工人采摘黑叶荔,则按(50﹣x)名工人采摘妃子笑,
y=4000×0.4x+5000×0.36×(50﹣x)=﹣200x+90000,
即y与x的函数关系式为y=﹣200x+90000(0≤x≤50);
(2)∵当天采摘的黑叶荔数量不少于的妃子笑数量,
∴0.4x≥0.36×(50﹣x),
解得,x≥23,
∵y=﹣200x+90000,
∴y随x的增大而减小,
又∵x为整数,
∴当x=24时,y取得最大值,此时y=85200,
答:若要求当天采摘的黑叶荔数量不少于的妃子笑数量,销售总额的最大值是85200元.
6.解:(1)设线段CD对应的函数表达式为y=kx+b.
将C(2,100)、D(4.5,400)代入y=kx+b中,得
解方程组得
所以线段CD所对应的函数表达式为y=120x﹣140(2≤x≤4.5).
(2)根据题意得,120x﹣140﹣80x=30,解得.
答:当x=时,轿车在货车前30千米.
7.解:(1)设y2与x的函数关系式为y=k2x+b2,根据题意得,
解得,
∴y2与x的函数关系式为y2=0.25x;
当0≤x≤180时,y1与x的函数关系式为y=0.5x;
当x>180时,设y1=k1+b1,根据题意得
,
解得,
∴y1与x的函数关系式为y1=0.6x﹣18;
∴;
(2)设王先生一家在高峰期用电x度,低谷期用电y度,
当0≤x≤180时,,
解得,不合题意,舍去;
当x>180时,,
解得.
答:王先生一家在高峰期用电230度,低谷期用电120度.
8.解:(1)用含x的式子表示从A往D市运
(
200﹣x
)t,
从B往C市运
(240﹣x)t,
从B往
D市运
(60+x)t,
(2)设总运费为W元,则有
W=20x+25(
200﹣x
)+15(240﹣x)+24(60+x)
=4x+10040,
∵0≤x≤200,W随x的增大而增大,
∴当x=0时,W有最小值,
即从A往D调200t,从B往D调60t,从B往C调240t时,总运费最少为10040元.
9.解:(1)由函数图象可得,
甲乙两地之间的路程是560km,快车的速度为:560÷(5﹣1)=140(km/h),慢车的速度为:560÷(5+4﹣1)=70(km/h),
故答案为:140,70;
(2)设出发a小时时,快慢两车相遇,
140a+70a=560,
解得,a=,
即出发小时后,快慢两车相遇,
故答案为:;
(3)快慢两车出发b小时后第一次相距150km,
140b+70b=560﹣150,
解得,b=,
即快慢两车出发小时后第一次相距150km
10.解:(1)由图象可知:学校和图书馆之间的距离为600米,亮亮用200秒骑车从图书馆到学校,而明明用300秒从到图书馆,
因此亮亮速度为:600÷200=3米/秒,明明的速度为600÷300=2米/秒,
故答案为:2,3.
(2)设明明的S1与t的关系式为S1=k1t,把(300,600)代入得:k1=2
∴S1=2t,
设亮亮的S2与t的关系式为S2=k2t+b,把(0,600)(200,0)代入得:
,解得:k2=﹣3,b=600,
∴S2=﹣3t+600,
答:明明、亮亮与学校的距离S1、S2与时间t的关系式分别为S1=2t,S2=﹣3t+600.
(3)当S1=S2时,即2t=﹣3t+600,解得t=120,即a=120s.
答:a的值为120秒.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
