六年级数学下册课件-6.2.1 图形的认识与测量人教版(共31张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.2.1 图形的认识与测量人教版(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 16:08:58 | ||
图片预览









文档简介
(共31张PPT)
图形的认识与测量
封闭图形一周的长度叫做这个图形的周长。
物体的表面或封闭图形的大小,叫做它们的面积。
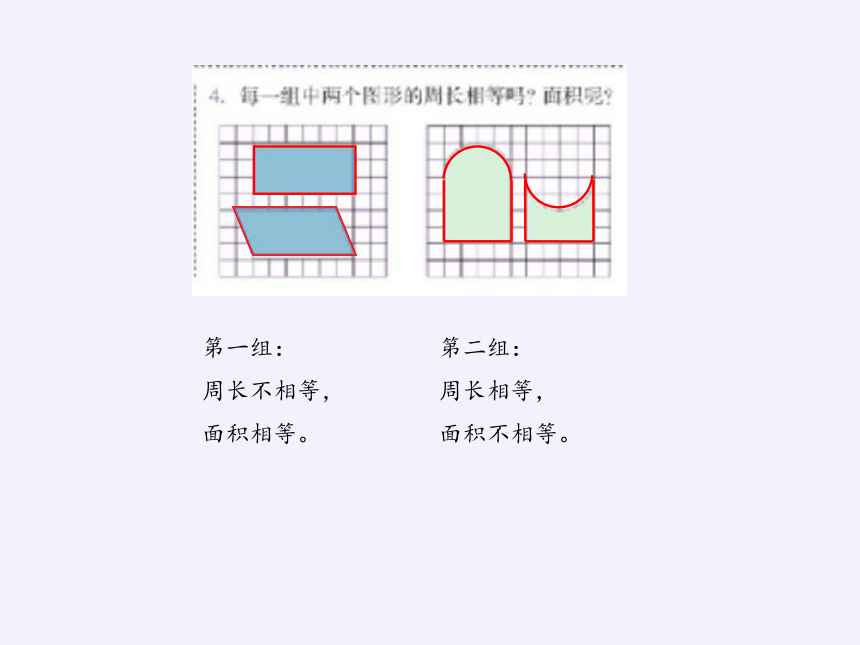
第一组:
周长不相等,
面积相等。
第二组:
周长相等,
面积不相等。
a
b
C
=
(a+b)×2
a
C
=
4a
r
C
=
?d
=
2?r
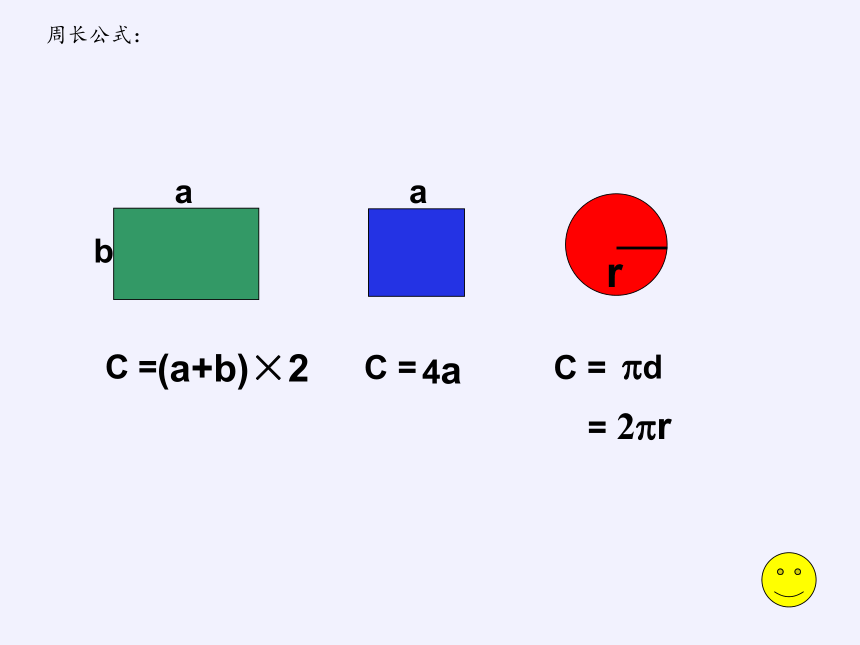
周长公式:
下面图形的面积计算公式是怎样推导出来的呢?
课前作业:
1.背诵视频中出现的所有公式。
2.认真填写课前导学卡,以备课前检查。
平面图形的周长和面积
潮州市潮安区实验学校
吴广
1.我们学过哪些平面图形?
请列举出来?
2.什么是平面图形的周长和面积?
用一个平面图形举例说说。
封闭图形一周的长度叫做这个图形的周长。
物体的表面或封闭图形的大小,叫做它们的面积。
3.我们已经学了哪些平面图形的周长计算公式?能用字母式子表示吗?
a
b
C
=
(a+b)×2
a
C
=
4a
r
C
=
?d
=
2?r
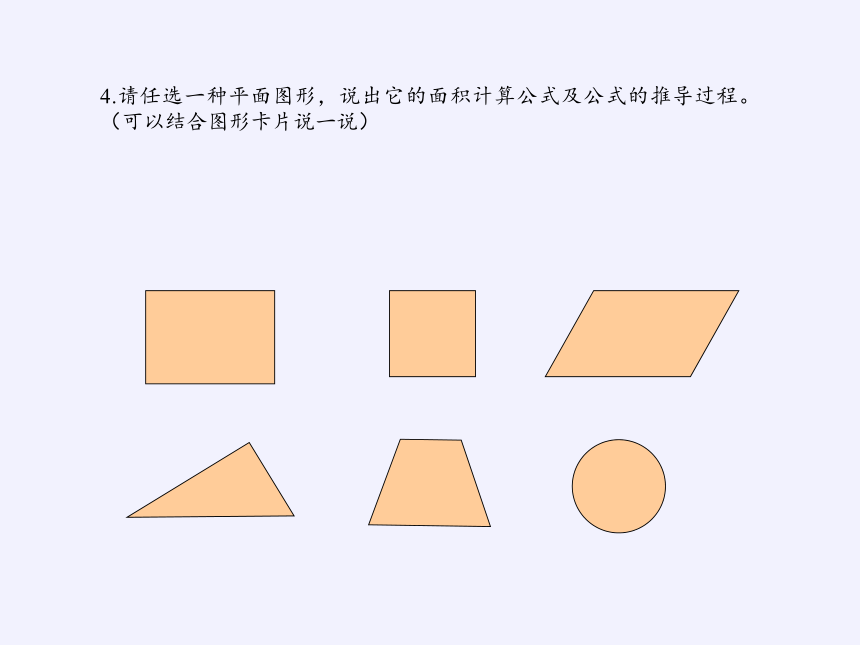
4.请任选一种平面图形,说出它的面积计算公式及公式的推导过程。(可以结合图形卡片说一说)
5.观察思考这些公式的推导过程,其中最主要是运用了哪种方法。
把新知识转化成已学知识进行认识、研究的思维方法。
转化:
(转化是学习数学的一种重要方法。)
6.根据公式推导中图形转化的联系进行分类整理。把图形摆一摆,贴在白纸上,最后连一连,形成网络图。说说为什么要这样摆!
(分类整理是复习数学的一种重要方法。)
C=2(a+b
)S=a
b
S=a
h÷2
S=a
h
S=(a+b)h÷2
C=πd
=2πr
S=
π
r
?
r
C=4a
S=a2
把面积、周长公式写在对应图形的旁边
7.根据公式中各个量的内在联系在整理图中写出相应的推导公式。说说你的推导思路!
例如:利用长方形周长求长。
=
C
(a+b)
×2
+b
a
=
C
÷2
a
=
C
÷2
-b
C=2(a+b
)
S=a
h÷2
S=a
h
S=(a+b)h÷2
C=πd=
2π
r
r
C=4a
S=a2
把面积、周长公式写在对应图形的旁边
a
=
C÷2
-
b
b
=
C÷2
-
a
a
=
S÷b
b
=
S÷a
a
=
C÷4
S=a
b
a
=
S÷h
h
=
S÷a
S=
π
r
?
d
=
C÷π
r
=
C÷π÷2
a
=
2S÷h
h
=
2S÷a
h
=
2S÷(a+b)
a
=
2S÷h
–
b
b
=
2S÷h
-
a
逻辑记忆法:把几个有内在联系的公式串联起来进行记忆。
8、计算图形的周长和面积。(单位:米)
6
10.5
7.5
6
30
40
50
4
(1)熊大绕着跑道跑一圈,跑了多少米?
(2)运动场是咱们班的卫生区域,请问打扫面积多大?
3.14
×
(60÷2)2
+100
×60
=2826+6000
=8826(平方米)
100米
60
米
3.14
×
60+100×
2=188.4+200=388.4(米)
生活中的数学
唐僧拿出三条一样长的绳子,叫三位徒弟用绳子各围一块地。
猪八戒急性子,嚷嚷说:“我要围成一个长方形。”
沙僧说:“我想围成正方形。”
孙悟空思考片刻,拍拍自己的脑袋说:“那我就围成圆形的吧!”
谁围的地最大?
谁围的面积大?
八戒:
沙僧:
悟空:
唐僧拿出三条都是62.8米长的绳子,
八戒围的长方形宽11.4米,面积是多少?
沙僧围的正方形面积是多少?
悟空围的圆形面积是多少?
(62.8÷2–11.4)×11.4
=228(㎡)
(62.8÷4)×(62.8÷4)=246.49(㎡)
3.14
×(62.8÷3.14÷2)
=314(㎡)
2
说一说
通过这节课的整理和复习,你有什么收获?
找出生活中你认识的平面图形,测量有关数据,求出它的周长和面积。
课外实践:
平行四边形面积公式的推导
底
高
(宽)
(长)
=
×
长方形的面积
平行四边形的面积
长
底
宽
高
=
×
平行四边形
长方形
转化
S
=
a
h
5
厘米
3
厘米
1平方厘米
=
×
面积单位的个数
长方形的面积
每排个数
长
排数
宽
=
×
长方形面积公式的推导
正方形面积公式的推导
因为正方形可以看作是长和宽相等的长方形。
边长
边长
长
宽
=
×
正方形的面积
长方形的面积
边长
长
边长
宽
=
×
三角形面积公式的推导
a
h
三角形的面积=平行四边形的面积÷2
三角形
平行四边形
转化
S
=
ah÷2
圆面积公式的推导
r
r
r
S=πr×r
=πr2
圆
近似长方形
转化
=πr
梯形面积公式的推导
a
b
h
梯形的面积=平行四边形的面积÷2
S
=(a+b)h÷2
梯形
平行四边形
转化
谢
谢
图形的认识与测量
封闭图形一周的长度叫做这个图形的周长。
物体的表面或封闭图形的大小,叫做它们的面积。
第一组:
周长不相等,
面积相等。
第二组:
周长相等,
面积不相等。
a
b
C
=
(a+b)×2
a
C
=
4a
r
C
=
?d
=
2?r
周长公式:
下面图形的面积计算公式是怎样推导出来的呢?
课前作业:
1.背诵视频中出现的所有公式。
2.认真填写课前导学卡,以备课前检查。
平面图形的周长和面积
潮州市潮安区实验学校
吴广
1.我们学过哪些平面图形?
请列举出来?
2.什么是平面图形的周长和面积?
用一个平面图形举例说说。
封闭图形一周的长度叫做这个图形的周长。
物体的表面或封闭图形的大小,叫做它们的面积。
3.我们已经学了哪些平面图形的周长计算公式?能用字母式子表示吗?
a
b
C
=
(a+b)×2
a
C
=
4a
r
C
=
?d
=
2?r
4.请任选一种平面图形,说出它的面积计算公式及公式的推导过程。(可以结合图形卡片说一说)
5.观察思考这些公式的推导过程,其中最主要是运用了哪种方法。
把新知识转化成已学知识进行认识、研究的思维方法。
转化:
(转化是学习数学的一种重要方法。)
6.根据公式推导中图形转化的联系进行分类整理。把图形摆一摆,贴在白纸上,最后连一连,形成网络图。说说为什么要这样摆!
(分类整理是复习数学的一种重要方法。)
C=2(a+b
)S=a
b
S=a
h÷2
S=a
h
S=(a+b)h÷2
C=πd
=2πr
S=
π
r
?
r
C=4a
S=a2
把面积、周长公式写在对应图形的旁边
7.根据公式中各个量的内在联系在整理图中写出相应的推导公式。说说你的推导思路!
例如:利用长方形周长求长。
=
C
(a+b)
×2
+b
a
=
C
÷2
a
=
C
÷2
-b
C=2(a+b
)
S=a
h÷2
S=a
h
S=(a+b)h÷2
C=πd=
2π
r
r
C=4a
S=a2
把面积、周长公式写在对应图形的旁边
a
=
C÷2
-
b
b
=
C÷2
-
a
a
=
S÷b
b
=
S÷a
a
=
C÷4
S=a
b
a
=
S÷h
h
=
S÷a
S=
π
r
?
d
=
C÷π
r
=
C÷π÷2
a
=
2S÷h
h
=
2S÷a
h
=
2S÷(a+b)
a
=
2S÷h
–
b
b
=
2S÷h
-
a
逻辑记忆法:把几个有内在联系的公式串联起来进行记忆。
8、计算图形的周长和面积。(单位:米)
6
10.5
7.5
6
30
40
50
4
(1)熊大绕着跑道跑一圈,跑了多少米?
(2)运动场是咱们班的卫生区域,请问打扫面积多大?
3.14
×
(60÷2)2
+100
×60
=2826+6000
=8826(平方米)
100米
60
米
3.14
×
60+100×
2=188.4+200=388.4(米)
生活中的数学
唐僧拿出三条一样长的绳子,叫三位徒弟用绳子各围一块地。
猪八戒急性子,嚷嚷说:“我要围成一个长方形。”
沙僧说:“我想围成正方形。”
孙悟空思考片刻,拍拍自己的脑袋说:“那我就围成圆形的吧!”
谁围的地最大?
谁围的面积大?
八戒:
沙僧:
悟空:
唐僧拿出三条都是62.8米长的绳子,
八戒围的长方形宽11.4米,面积是多少?
沙僧围的正方形面积是多少?
悟空围的圆形面积是多少?
(62.8÷2–11.4)×11.4
=228(㎡)
(62.8÷4)×(62.8÷4)=246.49(㎡)
3.14
×(62.8÷3.14÷2)
=314(㎡)
2
说一说
通过这节课的整理和复习,你有什么收获?
找出生活中你认识的平面图形,测量有关数据,求出它的周长和面积。
课外实践:
平行四边形面积公式的推导
底
高
(宽)
(长)
=
×
长方形的面积
平行四边形的面积
长
底
宽
高
=
×
平行四边形
长方形
转化
S
=
a
h
5
厘米
3
厘米
1平方厘米
=
×
面积单位的个数
长方形的面积
每排个数
长
排数
宽
=
×
长方形面积公式的推导
正方形面积公式的推导
因为正方形可以看作是长和宽相等的长方形。
边长
边长
长
宽
=
×
正方形的面积
长方形的面积
边长
长
边长
宽
=
×
三角形面积公式的推导
a
h
三角形的面积=平行四边形的面积÷2
三角形
平行四边形
转化
S
=
ah÷2
圆面积公式的推导
r
r
r
S=πr×r
=πr2
圆
近似长方形
转化
=πr
梯形面积公式的推导
a
b
h
梯形的面积=平行四边形的面积÷2
S
=(a+b)h÷2
梯形
平行四边形
转化
谢
谢
