六年级数学下册课件-6.1.3 式与方程-人教版(共23张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.1.3 式与方程-人教版(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 375.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
式与方程
看到这些字母你能立刻想到什么?
CCTV?? ?
?
UFO??????
?
NBA
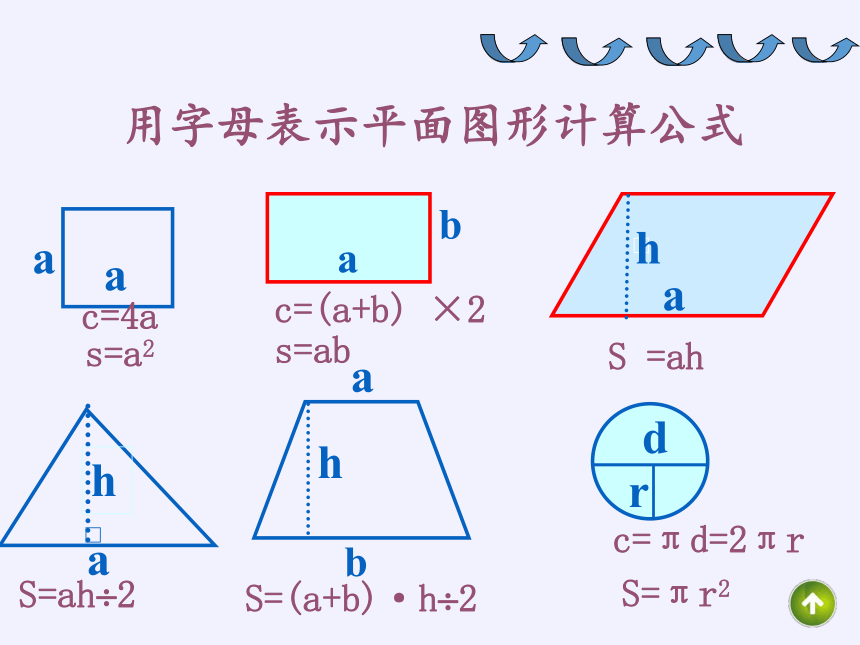
用字母表示平面图形计算公式
a
a
a
h
b
a
h
a
b
a
h
c=4a
S=ah?2
S=(a+b)·h?2
S
=ah
s=ab
c=πd=2πr
S=πr2
s=a2
c=(a+b)
×2
d
r
用字母表示数可以简明地表达数量关系
例如:
用s表示路程,v表示速度,t表示时间,那么
s=vt
c=at
如果工作总量用字母c表示,工作时间用t表示,工作效率用a表示,那么
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
用字母表示运算定律和性质
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷
(b×c)
1、用字母表示计算公式
2、用字母表示数量关系
3、用字母表示运算定律
用字母表示什么?
省略乘号,写出下面各式。
4×b
a×c
1×
χ
χ
χ
×
×5
χ
n×6
=4b
=5
χ
=
χ
χ
=
2
=
ac
=
6n
练
习
含有字母的式子的书写规则:
(1)字母和字母相乘,乘号可简写为“·”,也可省略不写。如果要省略,字母的先后顺序要尽量按字母表上的先后顺序。
如:x×y=x·y=xy
(2)数和字母相乘,乘号可简写为“·”,也可省略不写。如果要省略,数字要写在字母前面。
如:a×8=a·8=8a
(3)几个相同字母相乘可以写成字母的几次方。
如:a×a=a2
a×a×a=a3
(4)几个相同字母相加可以用乘法表示。
如:a+a=2a
a+a+a=3a
(5)1和字母相乘时,1省略不写。
如:1×a=a
(6)用含有字母的式子表示问题的答案或表示数量时,如果式子中有加号或减号,要用括号把含有字母的式子括起来。
如:小明有a岁,妈妈比他大24岁,妈妈有(a+24)岁。
学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9
ɑ表示
58
b表示
58-
ɑ表示
9
ɑ+
58
b表示
如果ɑ
=
45
,
b
=
6
则9
ɑ+
58
b=
9个足球的总价
b个篮球的总价
篮球的单价比足球的单价贵多少钱
学校买足球和篮球的总价钱
9×45+58×6=753
下面哪些是方程?哪些不是方程?
①
35-χ
=12
(
)
⑥
0.49÷χ
=7
(
)
②
Y+24
(
)
⑦
35+65=100
(
)
③
5
χ+32=47
(
)
⑧
χ-14>
72
(
)
④
28<
16+14
(
)
9b-3=60
(
)
⑤
6(a+2)=42
(
)
χ
+y=70
(
)
9
10
√
×
√
×
√
√
×
×
√
√
式子、等式和方程:
(1)像2+3、a-3、6b、a÷8、3+2=5、2x-8=10···用来表示几个数之间关系的,都叫做式子。
(2)像3+2=5、2x-8=10···这样表示左右两边相等的式子,都叫做等式。
(3)像x=2、3a+2=5、2x-8=10···这样含有未知数(x等字母)的等式,叫做方程。
式子、等式和方程三者之间的关系如下图
式子
等式
方程
方程是等式中的一部分;等式又是式子中的一部分。换句话说式子包含等式;等式包含方程。
1
2
x
+
6
=
20
X
=
7
解:2X
=
20
–
6
2x
=
14
x
=
14÷2
方程的解
求方程解的过程叫做解方程
方程的解和解方程:
(1)使方程左右两边相等的未知数的值,
叫做方程的解。
(2)求方程的解的过程叫做解方程。
方程的解是一个结果,如x=7。解方程是一个过程。
解方程的方法:
等式的性质:等式的左边和右边同时加上、减去、乘上、除以(不为0)一个数,左右两边仍然相等。
利用等式的基本性质,可以用于解方程。
另外,解比例方程就要用到比例的基本性质:两外项的积等于两内项的积。
先算的部分能直接计算的,先计算。
先算的部分含有x而不能算,把这部分当成一个整体。
几个地方有末知数的,先算。
括号里有末知数,先算但不能算,把括号看成一个整体。
小结:
(一)用字母表示数
用字母可以表示数、数量关系、
运算定律和计算公式等。
在含有字母的式子里,数字与字母,字母与字母相乘时乘号可以写作
“·”或省略不写,数字写在字母的前面。
小结:
(二)方程
含有未知数的等式叫做方程。
方程的解是使方程左右两边相等的未知数的值。
求方程的解的过程叫解方程。
v=abh
v=a3
v=sh
v=
a
b
h
a
h
s
s
h
用字母表示立体图形计算公式
=
谢
谢
式与方程
看到这些字母你能立刻想到什么?
CCTV?? ?
?
UFO??????
?
NBA
用字母表示平面图形计算公式
a
a
a
h
b
a
h
a
b
a
h
c=4a
S=ah?2
S=(a+b)·h?2
S
=ah
s=ab
c=πd=2πr
S=πr2
s=a2
c=(a+b)
×2
d
r
用字母表示数可以简明地表达数量关系
例如:
用s表示路程,v表示速度,t表示时间,那么
s=vt
c=at
如果工作总量用字母c表示,工作时间用t表示,工作效率用a表示,那么
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
用字母表示运算定律和性质
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷
(b×c)
1、用字母表示计算公式
2、用字母表示数量关系
3、用字母表示运算定律
用字母表示什么?
省略乘号,写出下面各式。
4×b
a×c
1×
χ
χ
χ
×
×5
χ
n×6
=4b
=5
χ
=
χ
χ
=
2
=
ac
=
6n
练
习
含有字母的式子的书写规则:
(1)字母和字母相乘,乘号可简写为“·”,也可省略不写。如果要省略,字母的先后顺序要尽量按字母表上的先后顺序。
如:x×y=x·y=xy
(2)数和字母相乘,乘号可简写为“·”,也可省略不写。如果要省略,数字要写在字母前面。
如:a×8=a·8=8a
(3)几个相同字母相乘可以写成字母的几次方。
如:a×a=a2
a×a×a=a3
(4)几个相同字母相加可以用乘法表示。
如:a+a=2a
a+a+a=3a
(5)1和字母相乘时,1省略不写。
如:1×a=a
(6)用含有字母的式子表示问题的答案或表示数量时,如果式子中有加号或减号,要用括号把含有字母的式子括起来。
如:小明有a岁,妈妈比他大24岁,妈妈有(a+24)岁。
学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9
ɑ表示
58
b表示
58-
ɑ表示
9
ɑ+
58
b表示
如果ɑ
=
45
,
b
=
6
则9
ɑ+
58
b=
9个足球的总价
b个篮球的总价
篮球的单价比足球的单价贵多少钱
学校买足球和篮球的总价钱
9×45+58×6=753
下面哪些是方程?哪些不是方程?
①
35-χ
=12
(
)
⑥
0.49÷χ
=7
(
)
②
Y+24
(
)
⑦
35+65=100
(
)
③
5
χ+32=47
(
)
⑧
χ-14>
72
(
)
④
28<
16+14
(
)
9b-3=60
(
)
⑤
6(a+2)=42
(
)
χ
+y=70
(
)
9
10
√
×
√
×
√
√
×
×
√
√
式子、等式和方程:
(1)像2+3、a-3、6b、a÷8、3+2=5、2x-8=10···用来表示几个数之间关系的,都叫做式子。
(2)像3+2=5、2x-8=10···这样表示左右两边相等的式子,都叫做等式。
(3)像x=2、3a+2=5、2x-8=10···这样含有未知数(x等字母)的等式,叫做方程。
式子、等式和方程三者之间的关系如下图
式子
等式
方程
方程是等式中的一部分;等式又是式子中的一部分。换句话说式子包含等式;等式包含方程。
1
2
x
+
6
=
20
X
=
7
解:2X
=
20
–
6
2x
=
14
x
=
14÷2
方程的解
求方程解的过程叫做解方程
方程的解和解方程:
(1)使方程左右两边相等的未知数的值,
叫做方程的解。
(2)求方程的解的过程叫做解方程。
方程的解是一个结果,如x=7。解方程是一个过程。
解方程的方法:
等式的性质:等式的左边和右边同时加上、减去、乘上、除以(不为0)一个数,左右两边仍然相等。
利用等式的基本性质,可以用于解方程。
另外,解比例方程就要用到比例的基本性质:两外项的积等于两内项的积。
先算的部分能直接计算的,先计算。
先算的部分含有x而不能算,把这部分当成一个整体。
几个地方有末知数的,先算。
括号里有末知数,先算但不能算,把括号看成一个整体。
小结:
(一)用字母表示数
用字母可以表示数、数量关系、
运算定律和计算公式等。
在含有字母的式子里,数字与字母,字母与字母相乘时乘号可以写作
“·”或省略不写,数字写在字母的前面。
小结:
(二)方程
含有未知数的等式叫做方程。
方程的解是使方程左右两边相等的未知数的值。
求方程的解的过程叫解方程。
v=abh
v=a3
v=sh
v=
a
b
h
a
h
s
s
h
用字母表示立体图形计算公式
=
谢
谢
