北师大版九年级 数学下册 第一章 直角三角形的边角关系复习教学设计
文档属性
| 名称 | 北师大版九年级 数学下册 第一章 直角三角形的边角关系复习教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 122.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
第一章
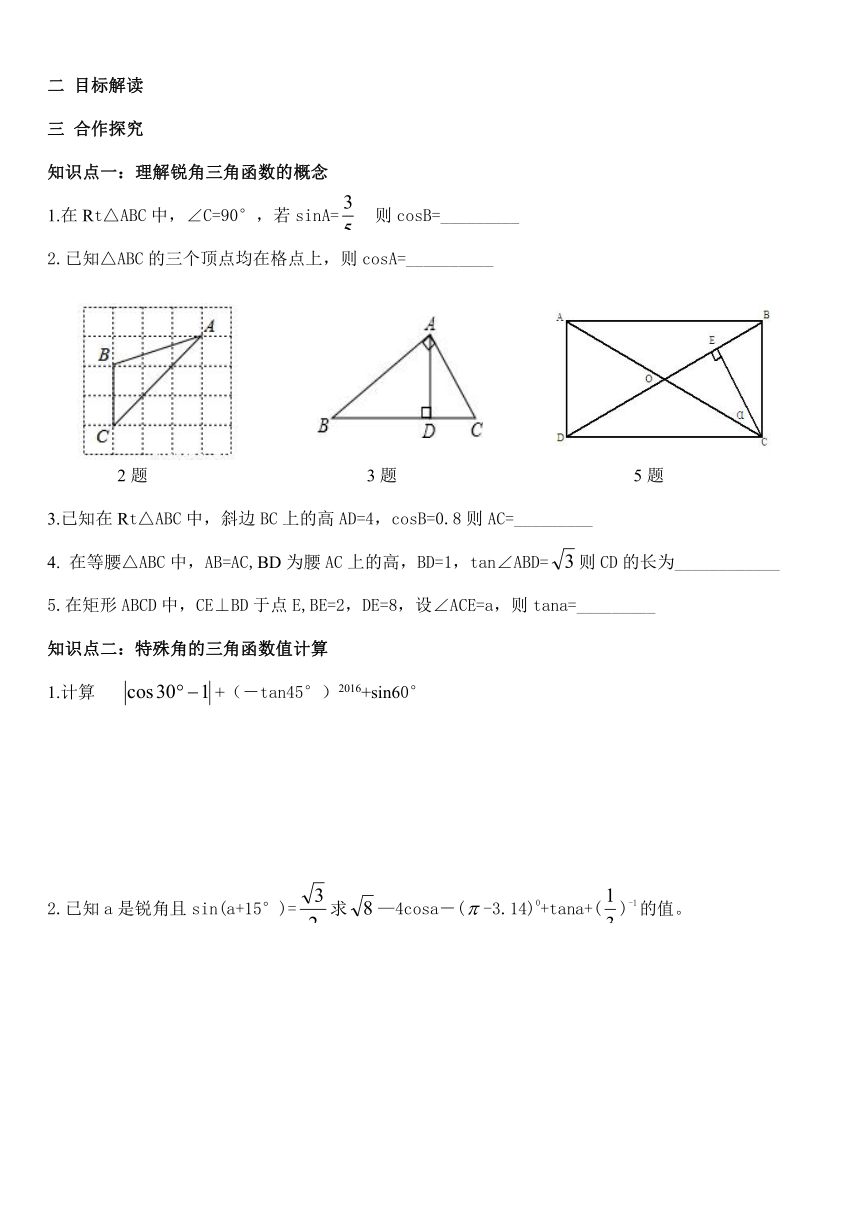
直角三角形的边角关系复习教学设计
【学习目标】1.理解锐角三角函数的概念
2.学会计算含有30°,45°,60°角的三角函数值
3.会运用锐角三角函数解直角三角形
4.应用三角函数知识解决生活中方向角,仰角,俯角,测量高等实际问题
【学习重点】理解锐角三角函数概念;会计算特殊角的三角函数值;能用锐角三角函数解直角三角形及解决一些简单的实际问题。
【知识链接】直角三角形的两锐角互余;勾股定理
【学习过程】
一
自主学习
二
目标解读
三
合作探究
知识点一:理解锐角三角函数的概念
1.在Rt△ABC中,∠C=90°,若sinA=
则cosB=_________
2.已知△ABC的三个顶点均在格点上,则cosA=__________
2题
3题
5题
3.已知在Rt△ABC中,斜边BC上的高AD=4,cosB=0.8则AC=_________
4.
在等腰△ABC中,AB=AC,BD为腰AC上的高,BD=1,tan∠ABD=则CD的长为____________
5.在矩形ABCD中,CE⊥BD于点E,BE=2,DE=8,设∠ACE=a,则tana=_________
知识点二:特殊角的三角函数值计算
1.计算
+(-tan45°)2016+sin60°
2.已知a是锐角且sin(a+15°)=求—4cosa-(-3.14)0+tana+()-1的值。
四
展示提升
知识点四:锐角三角函数的实际应
㈠.方向角问题
某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
(1)试说明点B是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
㈡.坡度、坡角问题
如图防洪大堤的横截面是梯形ABCD,其中AD∥BC,坡角a=60°汛期来临前对其进行了加固,改造后的背水面坡角β=45
0
,若原坡长AB=20m,求改造后的坡长AE(结果保留根号)
㈢仰角、俯角问题
如图小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高。(精确到0.1米,
≈1.732)
五
总结反馈
六
课外提升
仰角、俯角、坡度的综合应用
如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:
≈1.41,结果精确到0.1米)
【反思】
直角三角形的边角关系复习教学设计
【学习目标】1.理解锐角三角函数的概念
2.学会计算含有30°,45°,60°角的三角函数值
3.会运用锐角三角函数解直角三角形
4.应用三角函数知识解决生活中方向角,仰角,俯角,测量高等实际问题
【学习重点】理解锐角三角函数概念;会计算特殊角的三角函数值;能用锐角三角函数解直角三角形及解决一些简单的实际问题。
【知识链接】直角三角形的两锐角互余;勾股定理
【学习过程】
一
自主学习
二
目标解读
三
合作探究
知识点一:理解锐角三角函数的概念
1.在Rt△ABC中,∠C=90°,若sinA=
则cosB=_________
2.已知△ABC的三个顶点均在格点上,则cosA=__________
2题
3题
5题
3.已知在Rt△ABC中,斜边BC上的高AD=4,cosB=0.8则AC=_________
4.
在等腰△ABC中,AB=AC,BD为腰AC上的高,BD=1,tan∠ABD=则CD的长为____________
5.在矩形ABCD中,CE⊥BD于点E,BE=2,DE=8,设∠ACE=a,则tana=_________
知识点二:特殊角的三角函数值计算
1.计算
+(-tan45°)2016+sin60°
2.已知a是锐角且sin(a+15°)=求—4cosa-(-3.14)0+tana+()-1的值。
四
展示提升
知识点四:锐角三角函数的实际应
㈠.方向角问题
某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
(1)试说明点B是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
㈡.坡度、坡角问题
如图防洪大堤的横截面是梯形ABCD,其中AD∥BC,坡角a=60°汛期来临前对其进行了加固,改造后的背水面坡角β=45
0
,若原坡长AB=20m,求改造后的坡长AE(结果保留根号)
㈢仰角、俯角问题
如图小明为了测量小山顶的塔高,他在A处测得塔尖D的仰角为45°,再沿AC方向前进73.2米到达山脚B处,测得塔尖D的仰角为60°,塔底E的仰角为30°,求塔高。(精确到0.1米,
≈1.732)
五
总结反馈
六
课外提升
仰角、俯角、坡度的综合应用
如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据:
≈1.41,结果精确到0.1米)
【反思】
