11.1.2三角形的高、中线与角平分线-人教版八年级数学上册导学案
文档属性
| 名称 | 11.1.2三角形的高、中线与角平分线-人教版八年级数学上册导学案 |  | |
| 格式 | doc | ||
| 文件大小 | 91.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 07:27:02 | ||
图片预览

文档简介
11.1.2 三角形的高、中线与角平分线
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:认识三角形的高、中线与角平分线;会画三角形的高、中线与角平分线;了解三角形的三条高所在的直线,三条中线,三条角平分线分别交于一点.
2、过程与方法:经历画图的过程,在观察、操作、推理、归纳等过程中,发展合情推理能力.
3、情感、态度与价值观:体会数学与现实生活的联系,增强克服困难的勇气和信心.
学习重点:三角形的高、中线与角平分线.
学习难点:三角形的角平分线与角的平分线的区别,画钝角三角形的高.
学习过程:
一、自主学习:
(一)完成下面练习,并体验知识点的形成过程。
1、 定义:从三角形的一个 向它的 所在的直线作 , 和
之间的线段,叫做三角形的高。
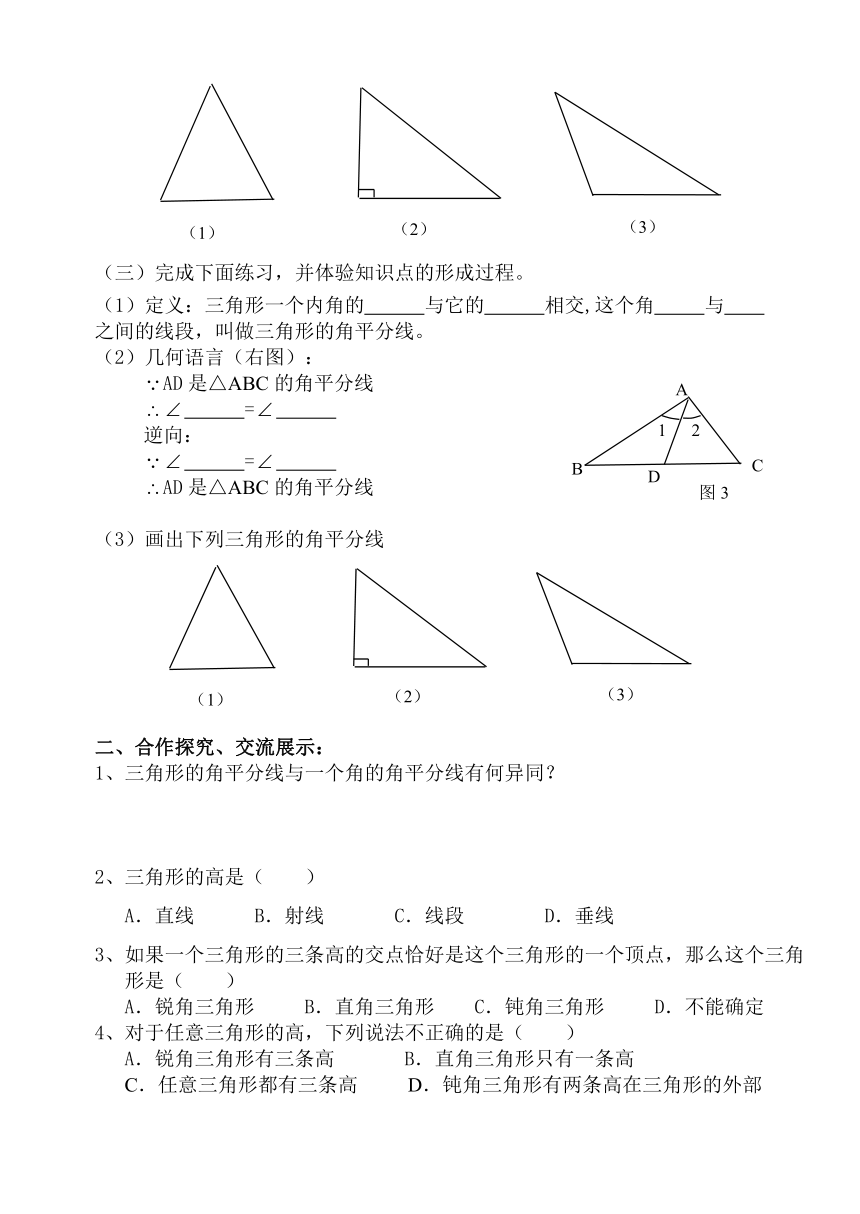
2、几何语言(图1)
AD是△ABC的高
ADBC于点D(或 = =90?)
逆向:
ADBC于点D(或 = =90?)
AD是△ABC中BC边上的高请画出下列三角形的高
A A A
B C B C B C
(二)完成下面练习,并体验知识点的形成过程。
(1)定义:连结三角形一个 和它对边 的线段,叫做三角形的中线。
(2)几何语言(右图)
AD是△ABC的中线
=
逆向:
=
AD是△ABC的中线
(3)画出下列三角形的中线
(三)完成下面练习,并体验知识点的形成过程。
(1)定义:三角形一个内角的 与它的 相交,这个角 与
之间的线段,叫做三角形的角平分线。
(2)几何语言(右图):
AD是△ABC的角平分线
=
逆向:
=
AD是△ABC的角平分线
(3)画出下列三角形的角平分线
二、合作探究、交流展示:
1、三角形的角平分线与一个角的角平分线有何异同?
2、三角形的高是( )
A.直线 B.射线 C.线段 D.垂线
3、如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
4、对于任意三角形的高,下列说法不正确的是( )
A.锐角三角形有三条高 B.直角三角形只有一条高
C.任意三角形都有三条高 D.钝角三角形有两条高在三角形的外部
三、拓展延伸:
在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm两部分,求三角形各边的长.
四、课堂检测:
1、如图1,在△ABC中,∠ACB=900,CD是边AB上的高。与∠A相等的角是( )
A.∠A B.∠ACD C.∠BCD D.∠BDC
C
A B
D
图1 图2
2、如图2,在锐角△ABC中,CD、BE分别是AB、AC上的高,且CD、BE交于一
点P,若∠A=50°,则∠BPC的度数是( )
A.150° B.130° C.120° D.100°
3、如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5, BE⊥AC于E,求BE
的长.
五、学(教)后反思:
答案
一、自主学习:
(一)1、 顶点,对边,垂线,顶点,垂足
2、∠ADB=∠ADC,∠ADB=∠ADC 图略
(二)(1)顶点,中点
(2)BD=CD,BD=CD (3)图略
(三)(1)平分线,对边,顶点,交点
(2)1=2,1=2 (3)略
二、合作探究、交流展示:
1、解:角平分线:在角的内部,把角分成两个相等的角的一条射线,
三角形的角平分线:三角形内角平分线与对边交点之间的线段,叫做三角形的角平分线
最大区别是:角平分线是一条射线,而三角形的角平分线是一条线段
2、C 3、 B 4、B
三、拓展延伸:
解:如图:
(1)当AB与AD的和是12厘米时
AD=12÷(1+2)=12÷3=4(厘米)
所以AB=AC=2×4=8(厘米)
BC=12+15?8×2=12+15?16=11(厘米)
(2)当AB与AD的和是15厘米时
AD=15÷(1+2)=12÷3=5(厘米)
所以AB=AC=2×5=10(厘米)
BC=12+15?10×2=12+15?20=7(厘米)
答:三角形的三角形可能是8厘米,8厘米,11厘米或10厘米,10厘米,7厘米。
四、课堂检测:
1、C 2、B
3、解:∵SABC=AC?BE,SABC=BC?AD,
∴AC?BE=BC?AD,
∴BE==.
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:认识三角形的高、中线与角平分线;会画三角形的高、中线与角平分线;了解三角形的三条高所在的直线,三条中线,三条角平分线分别交于一点.
2、过程与方法:经历画图的过程,在观察、操作、推理、归纳等过程中,发展合情推理能力.
3、情感、态度与价值观:体会数学与现实生活的联系,增强克服困难的勇气和信心.
学习重点:三角形的高、中线与角平分线.
学习难点:三角形的角平分线与角的平分线的区别,画钝角三角形的高.
学习过程:
一、自主学习:
(一)完成下面练习,并体验知识点的形成过程。
1、 定义:从三角形的一个 向它的 所在的直线作 , 和
之间的线段,叫做三角形的高。
2、几何语言(图1)
AD是△ABC的高
ADBC于点D(或 = =90?)
逆向:
ADBC于点D(或 = =90?)
AD是△ABC中BC边上的高请画出下列三角形的高
A A A
B C B C B C
(二)完成下面练习,并体验知识点的形成过程。
(1)定义:连结三角形一个 和它对边 的线段,叫做三角形的中线。
(2)几何语言(右图)
AD是△ABC的中线
=
逆向:
=
AD是△ABC的中线
(3)画出下列三角形的中线
(三)完成下面练习,并体验知识点的形成过程。
(1)定义:三角形一个内角的 与它的 相交,这个角 与
之间的线段,叫做三角形的角平分线。
(2)几何语言(右图):
AD是△ABC的角平分线
=
逆向:
=
AD是△ABC的角平分线
(3)画出下列三角形的角平分线
二、合作探究、交流展示:
1、三角形的角平分线与一个角的角平分线有何异同?
2、三角形的高是( )
A.直线 B.射线 C.线段 D.垂线
3、如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
4、对于任意三角形的高,下列说法不正确的是( )
A.锐角三角形有三条高 B.直角三角形只有一条高
C.任意三角形都有三条高 D.钝角三角形有两条高在三角形的外部
三、拓展延伸:
在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12cm和15cm两部分,求三角形各边的长.
四、课堂检测:
1、如图1,在△ABC中,∠ACB=900,CD是边AB上的高。与∠A相等的角是( )
A.∠A B.∠ACD C.∠BCD D.∠BDC
C
A B
D
图1 图2
2、如图2,在锐角△ABC中,CD、BE分别是AB、AC上的高,且CD、BE交于一
点P,若∠A=50°,则∠BPC的度数是( )
A.150° B.130° C.120° D.100°
3、如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5, BE⊥AC于E,求BE
的长.
五、学(教)后反思:
答案
一、自主学习:
(一)1、 顶点,对边,垂线,顶点,垂足
2、∠ADB=∠ADC,∠ADB=∠ADC 图略
(二)(1)顶点,中点
(2)BD=CD,BD=CD (3)图略
(三)(1)平分线,对边,顶点,交点
(2)1=2,1=2 (3)略
二、合作探究、交流展示:
1、解:角平分线:在角的内部,把角分成两个相等的角的一条射线,
三角形的角平分线:三角形内角平分线与对边交点之间的线段,叫做三角形的角平分线
最大区别是:角平分线是一条射线,而三角形的角平分线是一条线段
2、C 3、 B 4、B
三、拓展延伸:
解:如图:
(1)当AB与AD的和是12厘米时
AD=12÷(1+2)=12÷3=4(厘米)
所以AB=AC=2×4=8(厘米)
BC=12+15?8×2=12+15?16=11(厘米)
(2)当AB与AD的和是15厘米时
AD=15÷(1+2)=12÷3=5(厘米)
所以AB=AC=2×5=10(厘米)
BC=12+15?10×2=12+15?20=7(厘米)
答:三角形的三角形可能是8厘米,8厘米,11厘米或10厘米,10厘米,7厘米。
四、课堂检测:
1、C 2、B
3、解:∵SABC=AC?BE,SABC=BC?AD,
∴AC?BE=BC?AD,
∴BE==.
