11.3.1多边形及其内角和-人教版八年级数学上册导学案
文档属性
| 名称 | 11.3.1多边形及其内角和-人教版八年级数学上册导学案 | 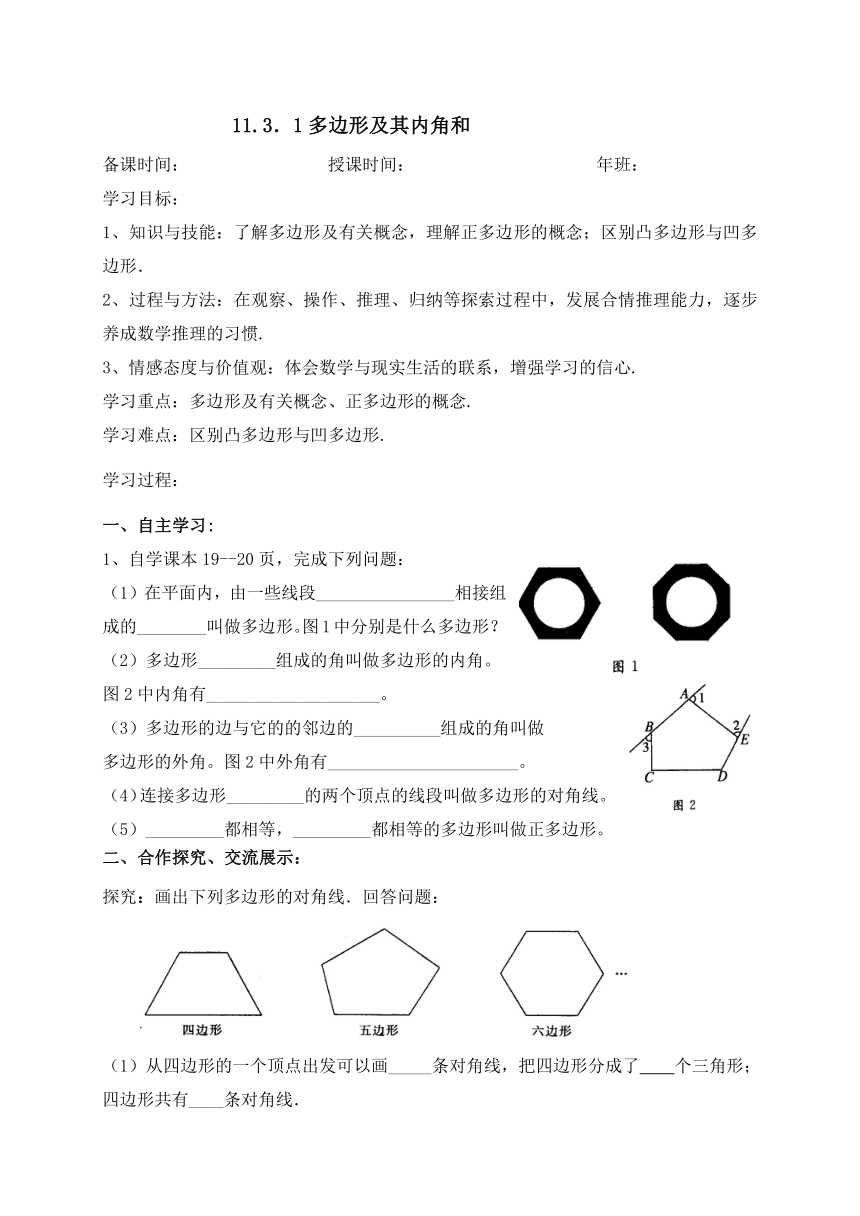 | |
| 格式 | doc | ||
| 文件大小 | 45.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 07:29:36 | ||
图片预览

文档简介
11.3.1多边形及其内角和
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:了解多边形及有关概念,理解正多边形的概念;区别凸多边形与凹多边形.
2、过程与方法:在观察、操作、推理、归纳等探索过程中,发展合情推理能力,逐步养成数学推理的习惯.
3、情感态度与价值观:体会数学与现实生活的联系,增强学习的信心.
学习重点:多边形及有关概念、正多边形的概念.
学习难点:区别凸多边形与凹多边形.
学习过程:
一、自主学习:
1、自学课本19--20页,完成下列问题:
(1)在平面内,由一些线段________________相接组成的________叫做多边形。图1中分别是什么多边形?
(2)多边形_________组成的角叫做多边形的内角。图2中内角有____________________。
(3)多边形的边与它的的邻边的__________组成的角叫做
多边形的外角。图2中外角有______________________。
(4)连接多边形_________的两个顶点的线段叫做多边形的对角线。
(5)_________都相等,_________都相等的多边形叫做正多边形。
二、合作探究、交流展示:
探究:画出下列多边形的对角线.回答问题:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线.
(4)猜想:①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形,100边形共有___条对角线.②从n边形的一个顶点出发可以画_____条对角线,把n分成了 个三角形;n边形共有_____条对角线.
三、拓展延伸:
(1)从n边形的一个顶点出发可作______条对角线,从n边形n个顶点出发可作_____条对角线,除去重复作的对角线,则n边形的对角线的总数为_____条.
(2)过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则(m-k)=________.
(3)过十边形的一个顶点可作出几条对角线?把十边形分成了几个三角形?
(4)十二边形共有 条对角线,过一个顶点可作 条对角线,可把十二边形分成 个三角形。
四、课堂检测:
1、下列图形中,是正多边形的是( )
A.直角三角形 B.等腰三角形 C.长方形 D.正方形
2、九边形的对角线有( )
A.25条 B.31条 C.27条 D.30条
3、已知的的外角平分线交于点D,,那么=
4、在中等于和它相邻的外角的四分之一,这个外角等于的两倍,那么 , ,
五、学(教)后反思:
答案
一、自主学习:
1、(1)首尾顺次,封闭图形
(2)相邻两边
(3)延长线
(4)不相邻
(5)各个角,各条边
二、合作探究、交流展示:
图略
(1)1,2,2
(2)2,3,5
(3)3,4,9
(4)① 97,98,4850 ② n-3,n-2,
三、拓展延伸:
(1)n-3,n(n-3),
(2)6
(3)7,8
(4)54,9,10
四、课堂检测:
1、D
2、C
3、110°
4、36°, 72°,72°
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:了解多边形及有关概念,理解正多边形的概念;区别凸多边形与凹多边形.
2、过程与方法:在观察、操作、推理、归纳等探索过程中,发展合情推理能力,逐步养成数学推理的习惯.
3、情感态度与价值观:体会数学与现实生活的联系,增强学习的信心.
学习重点:多边形及有关概念、正多边形的概念.
学习难点:区别凸多边形与凹多边形.
学习过程:
一、自主学习:
1、自学课本19--20页,完成下列问题:
(1)在平面内,由一些线段________________相接组成的________叫做多边形。图1中分别是什么多边形?
(2)多边形_________组成的角叫做多边形的内角。图2中内角有____________________。
(3)多边形的边与它的的邻边的__________组成的角叫做
多边形的外角。图2中外角有______________________。
(4)连接多边形_________的两个顶点的线段叫做多边形的对角线。
(5)_________都相等,_________都相等的多边形叫做正多边形。
二、合作探究、交流展示:
探究:画出下列多边形的对角线.回答问题:
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线.
(4)猜想:①从100边形的一个顶点出发可以画_____条对角线,把100边形分成了 个三角形,100边形共有___条对角线.②从n边形的一个顶点出发可以画_____条对角线,把n分成了 个三角形;n边形共有_____条对角线.
三、拓展延伸:
(1)从n边形的一个顶点出发可作______条对角线,从n边形n个顶点出发可作_____条对角线,除去重复作的对角线,则n边形的对角线的总数为_____条.
(2)过m边形的一个顶点有7条对角线,n边形没有对角线,k边形有2条对角线,则(m-k)=________.
(3)过十边形的一个顶点可作出几条对角线?把十边形分成了几个三角形?
(4)十二边形共有 条对角线,过一个顶点可作 条对角线,可把十二边形分成 个三角形。
四、课堂检测:
1、下列图形中,是正多边形的是( )
A.直角三角形 B.等腰三角形 C.长方形 D.正方形
2、九边形的对角线有( )
A.25条 B.31条 C.27条 D.30条
3、已知的的外角平分线交于点D,,那么=
4、在中等于和它相邻的外角的四分之一,这个外角等于的两倍,那么 , ,
五、学(教)后反思:
答案
一、自主学习:
1、(1)首尾顺次,封闭图形
(2)相邻两边
(3)延长线
(4)不相邻
(5)各个角,各条边
二、合作探究、交流展示:
图略
(1)1,2,2
(2)2,3,5
(3)3,4,9
(4)① 97,98,4850 ② n-3,n-2,
三、拓展延伸:
(1)n-3,n(n-3),
(2)6
(3)7,8
(4)54,9,10
四、课堂检测:
1、D
2、C
3、110°
4、36°, 72°,72°
