11.3.2多边形的内角和-人教版八年级数学上册导学案
文档属性
| 名称 | 11.3.2多边形的内角和-人教版八年级数学上册导学案 | 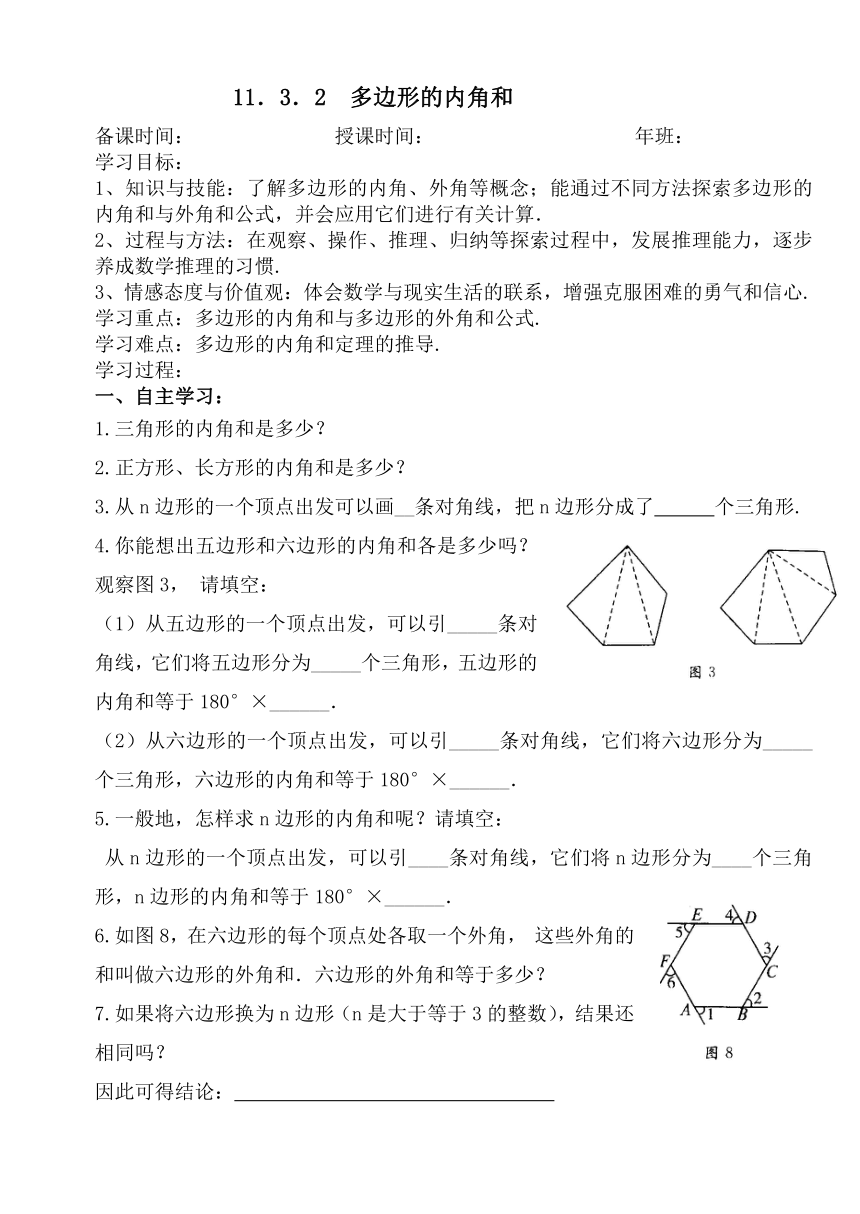 | |
| 格式 | doc | ||
| 文件大小 | 36.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 07:32:38 | ||
图片预览

文档简介
11.3.2 多边形的内角和
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:了解多边形的内角、外角等概念;能通过不同方法探索多边形的内角和与外角和公式,并会应用它们进行有关计算.
2、过程与方法:在观察、操作、推理、归纳等探索过程中,发展推理能力,逐步养成数学推理的习惯.
3、情感态度与价值观:体会数学与现实生活的联系,增强克服困难的勇气和信心.
学习重点:多边形的内角和与多边形的外角和公式.
学习难点:多边形的内角和定理的推导.
学习过程:
一、自主学习:
1.三角形的内角和是多少?
2.正方形、长方形的内角和是多少?
3.从n边形的一个顶点出发可以画__条对角线,把n边形分成了 个三角形.
4.你能想出五边形和六边形的内角和各是多少吗?观察图3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×______.
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×______.
5.一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引____条对角线,它们将n边形分为____个三角形,n边形的内角和等于180°×______.
6.如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
7.如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论:
二、合作探究、交流展示:
1、已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形。
2、如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别为________。
3、一个多边形的每一个外角都等于40°,则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是___________。
4、七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______。
5、一个多边形的每一个外角都等于36°则这个多边形是_______边形。
6、在每个内角都相等的多边形中,若一个外角是它相邻内角的,则这个多边形是______边形。
7、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
三、拓展延伸:
1、当一个多边形的边数增加1时,它的内角和增加_________度.
2、 正十边形的一个外角为______.
3、_______边形的内角和与外角和相等.
四、课堂检测:
1、若四边形的四个内角大小之比为1:2:3:4,则这四个内角的大小为 。
2、如果六边形的各个内角都相等,那么它的一个内角是 。
3、在各个内角都相等的多边形中,一个外角等于一个内角的,则这个多边形的每个内角为 度。
4、(n+1)边形的内角和比n边形的内角和大( )。
A: 180° B: 360° C:n×180° D: n×360°
5、n边形的内角中,最多有( )个锐角。
A:1个 B: 2 个 C: 3个 D: 4个
6、若多边形内角和分别为下列度数时,试分别求出多边形的边数。
1260° ② 2160°
7、已知n边形的内角和与外角和之比为9:2,求n。
五、学(教)后反思:
答案
一、自主学习:
1.180°
2.360°
n-3,n-2
4.(1)2,3,3
(2)3,4,4
5.n-3,n-2,n-2
6.360°
7.多边形的外角和等于360°
二、合作探究、交流展示:
1、十
2、60°,90°,120°
3、9,9
4、360°,360°,360°
十
6、六
7、9
三、拓展延伸:
1、180°
2、 36°
3、四
四、课堂检测:
1、36°,72°,108°144°
2、120°
3、35°
4、A
5、C
6、①9 ② 14
7、11
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:了解多边形的内角、外角等概念;能通过不同方法探索多边形的内角和与外角和公式,并会应用它们进行有关计算.
2、过程与方法:在观察、操作、推理、归纳等探索过程中,发展推理能力,逐步养成数学推理的习惯.
3、情感态度与价值观:体会数学与现实生活的联系,增强克服困难的勇气和信心.
学习重点:多边形的内角和与多边形的外角和公式.
学习难点:多边形的内角和定理的推导.
学习过程:
一、自主学习:
1.三角形的内角和是多少?
2.正方形、长方形的内角和是多少?
3.从n边形的一个顶点出发可以画__条对角线,把n边形分成了 个三角形.
4.你能想出五边形和六边形的内角和各是多少吗?观察图3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角线,它们将五边形分为_____个三角形,五边形的内角和等于180°×______.
(2)从六边形的一个顶点出发,可以引_____条对角线,它们将六边形分为_____个三角形,六边形的内角和等于180°×______.
5.一般地,怎样求n边形的内角和呢?请填空:
从n边形的一个顶点出发,可以引____条对角线,它们将n边形分为____个三角形,n边形的内角和等于180°×______.
6.如图8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
7.如果将六边形换为n边形(n是大于等于3的整数),结果还相同吗?
因此可得结论:
二、合作探究、交流展示:
1、已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形。
2、如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别为________。
3、一个多边形的每一个外角都等于40°,则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是___________。
4、七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______。
5、一个多边形的每一个外角都等于36°则这个多边形是_______边形。
6、在每个内角都相等的多边形中,若一个外角是它相邻内角的,则这个多边形是______边形。
7、若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。
三、拓展延伸:
1、当一个多边形的边数增加1时,它的内角和增加_________度.
2、 正十边形的一个外角为______.
3、_______边形的内角和与外角和相等.
四、课堂检测:
1、若四边形的四个内角大小之比为1:2:3:4,则这四个内角的大小为 。
2、如果六边形的各个内角都相等,那么它的一个内角是 。
3、在各个内角都相等的多边形中,一个外角等于一个内角的,则这个多边形的每个内角为 度。
4、(n+1)边形的内角和比n边形的内角和大( )。
A: 180° B: 360° C:n×180° D: n×360°
5、n边形的内角中,最多有( )个锐角。
A:1个 B: 2 个 C: 3个 D: 4个
6、若多边形内角和分别为下列度数时,试分别求出多边形的边数。
1260° ② 2160°
7、已知n边形的内角和与外角和之比为9:2,求n。
五、学(教)后反思:
答案
一、自主学习:
1.180°
2.360°
n-3,n-2
4.(1)2,3,3
(2)3,4,4
5.n-3,n-2,n-2
6.360°
7.多边形的外角和等于360°
二、合作探究、交流展示:
1、十
2、60°,90°,120°
3、9,9
4、360°,360°,360°
十
6、六
7、9
三、拓展延伸:
1、180°
2、 36°
3、四
四、课堂检测:
1、36°,72°,108°144°
2、120°
3、35°
4、A
5、C
6、①9 ② 14
7、11
