沪教版(上海)数学八年级第二学期-22.6 三角形、梯形的中位线(1) 课件(共20张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.6 三角形、梯形的中位线(1) 课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 385.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览


文档简介
(共20张PPT)
§22.6三角形、梯形的中位线(1)
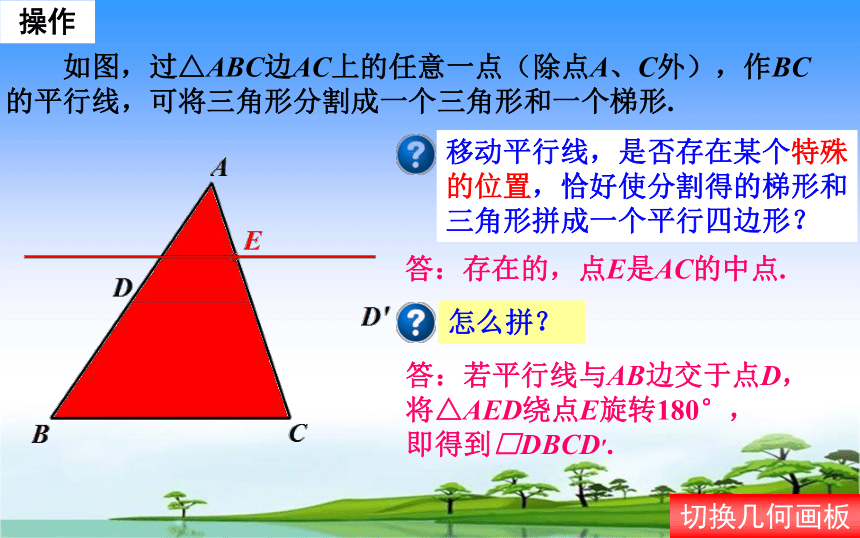
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
移动平行线,是否存在某个特殊
的位置,恰好使分割得的梯形和
三角形拼成一个平行四边形?
答:存在的,点E是AC的中点.
怎么拼?
答:若平行线与AB边交于点D,
将△AED绕点E旋转180°,
即得到□DBCD′.
切换几何画板
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
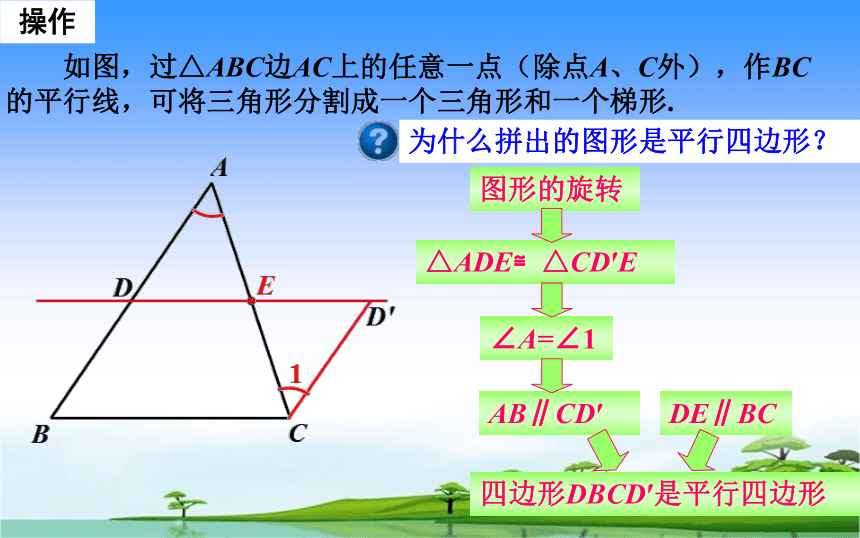
为什么拼出的图形是平行四边形?
图形的旋转
△ADE≌△CD′E
∠A=∠1
AB∥CD′
DE∥BC
四边形DBCD′是平行四边形
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
这时,点D位于线段AB的什么位置上?
答:由于CD′=DB
,且CD′=AD,所以AD=BD,点D是AB的中点.
点D、E分别是△ABC的边AB、AC的中点,
则线段DE是△ABC的一条特殊线段.
为什么拼出的图形是平行四边形?
三角形中位线的概念
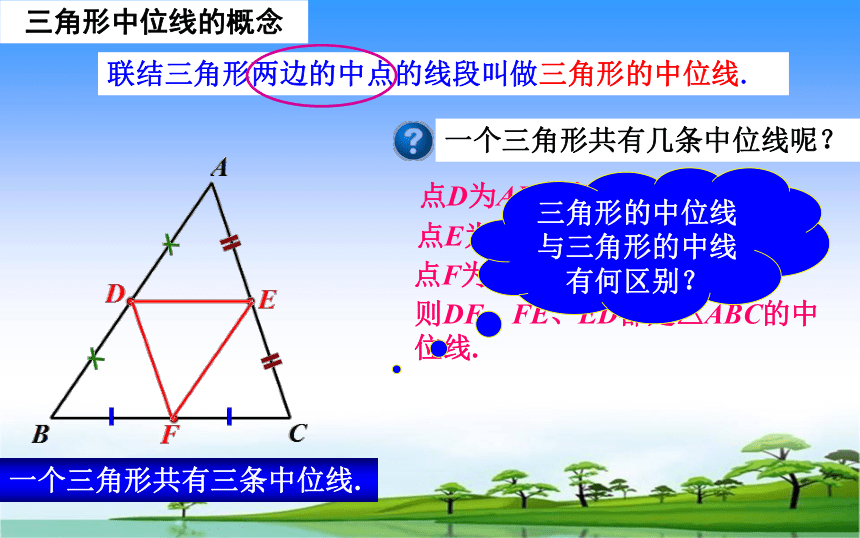
联结三角形两边的中点的线段叫做三角形的中位线.
一个三角形共有几条中位线呢?
点D为AB中点,
点E为AC中点,
点F为BC中点,
则DF、FE、ED都是△ABC的中位线.
一个三角形共有三条中位线.
三角形的中位线与三角形的中线有何区别?
适时小结
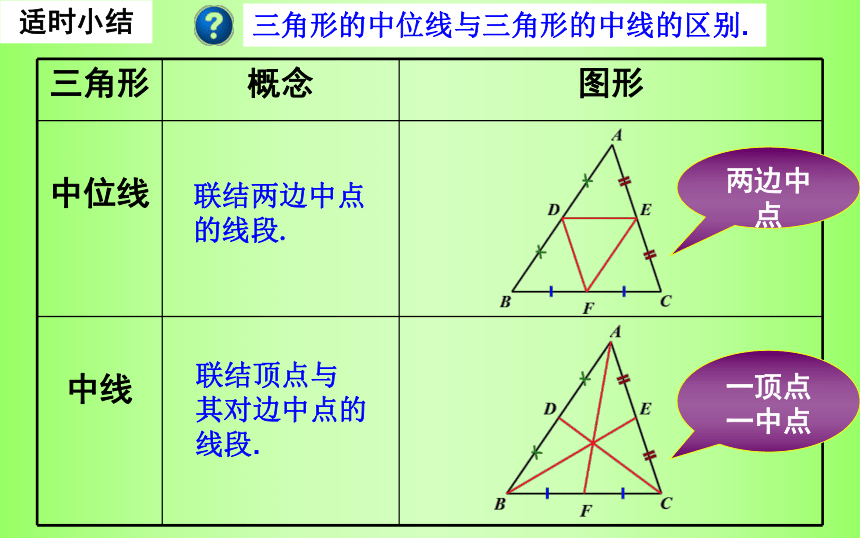
三角形的中位线与三角形的中线的区别.
三角形
概念
图形
中位线
中线
联结两边中点的线段.
联结顶点与
其对边中点的线段.
两边中点
一顶点
一中点
学习三角形中位线定理
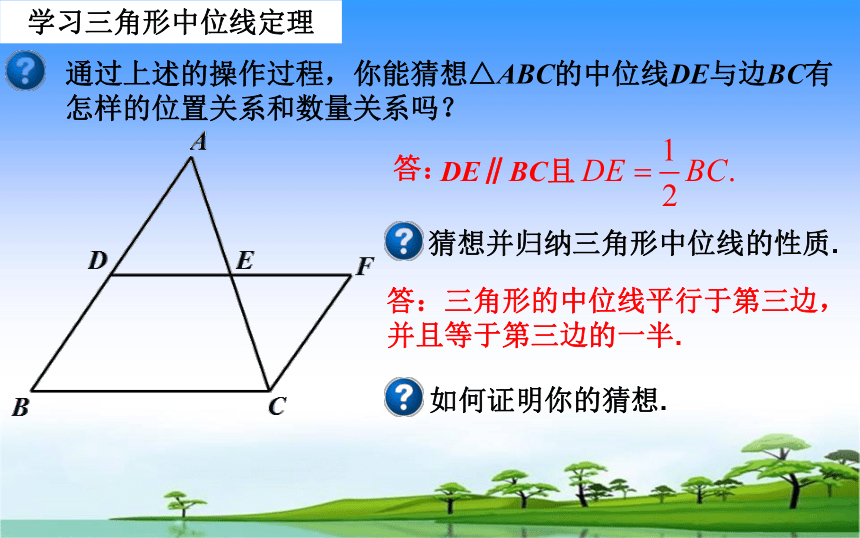
通过上述的操作过程,你能猜想△ABC的中位线DE与边BC有
怎样的位置关系和数量关系吗?
DE∥BC且
答:
猜想并归纳三角形中位线的性质.
如何证明你的猜想.
答:三角形的中位线平行于第三边,
并且等于第三边的一半.
如何证明四边形DBCF是平行四边形?
∴四边形BCFD是平行四边形
(一组对边平行且相等的四边形是平行四边形),
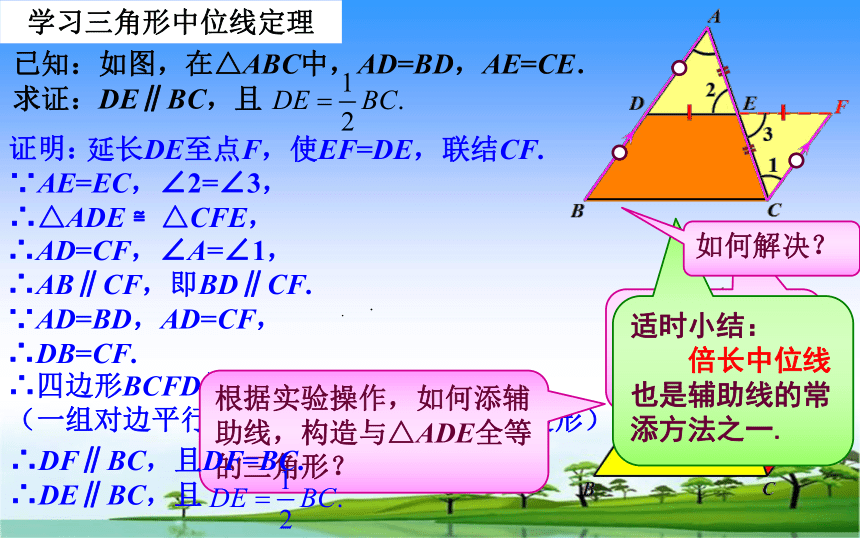
根据实验操作,如何添辅助线,构造与△ADE全等的三角形?
已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且
.
延长DE至点F,使EF=DE,联结CF.
证明:
∵AE=EC,∠2=∠3,
∴△ADE
≌△CFE,
∴AD=CF,∠A=∠1,
∴AB∥CF,即BD∥CF.
∵AD=BD,AD=CF,
∴DB=CF.
∴DF∥BC,且DF=BC.
∴DE∥BC,且
.
适时小结:
倍长中位线也是辅助线的常添方法之一.
学习三角形中位线定理
如何解决?
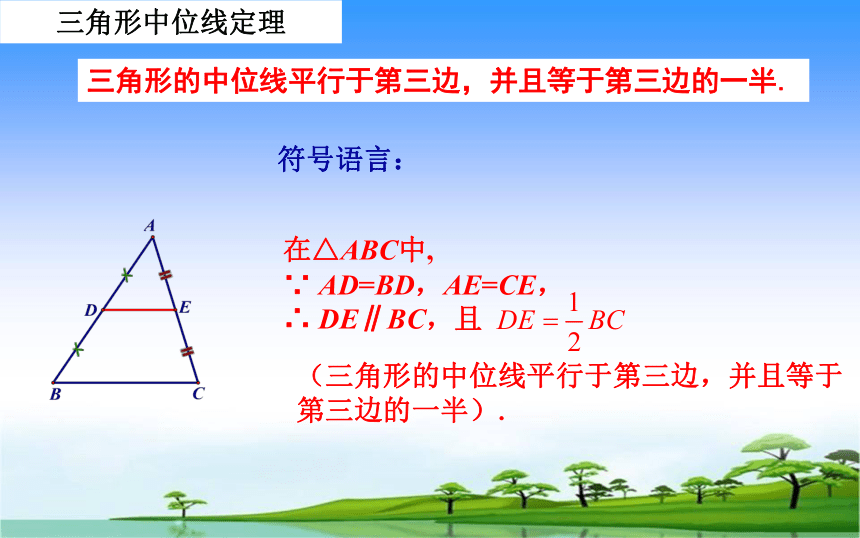
三角形中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
在△ABC中,
∵
AD=BD,AE=CE,
∴
DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
符号语言:
新知运用
(2)如果DE=5,那么BC=____.
10
(一)口答练习
1、如图,已知AD=DB,AE=EC,
(1)如果BC=
,那么DE=____;
新知运用
2、如图,B、C两点被海水隔开,在B、C外选择一点A,找到AB、AC的中点E、F,测量得EF=22米.这样就能求出B、C两点间的距离.请说出这是为什么?
答:∵
点E、F分别为AB、AC的中点,
∴
EF∥BC,且BC=2EF=44米
(三角形的中位线平行于第三边,
并且等于第三边的一半).
例题讲解
例题6
已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、
OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
由已知条件你能在图中找到什么?
GF、DE分别是△ABC和△OBC的中位线,且这两个三角形有公共边BC.
如何证明?
例题讲解
例题6
已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、
OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
证明:∵
点G、F分别为AB、AC的中点,
∴
GF∥BC,且
(三角形的中位线平行于第三边,
并且等于第三边的一半).
同理:DE∥BC,且
.
∴GF∥DE,且GF=DE.
∴四边形DEFG是平行四边形
(一组对边平行且相等的四边形是平行四边形).
变式2:顺次联结四边形四条边的中点,所得的四边形(称为“中点四边形”),是平行四边形吗?
分析:
例题讲解
例题6
已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、
OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
变式1:如图,点O是△ABC外一点,以上结论是否还成立?
答:成立.
变
点O的位置
不变
GF、DE仍是△ABC和△OBC的中位线,且这两个三角形有公共边BC.
结论
四边形DEFG是平行四边形.
答:是的.
如何证明?
方法类似.
形变质不变
课堂练习
求证:顺次联结四边形四条边的中点,所得的四边形是平行四边形.
已知:如图,四边形ABCD中,
E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形DEFG是平行四边形.
证明:联结BD.
适时小结
1、以上的三个问题图形变化,而本质是不变的.
2、任意四边形的“中点四边形”是平行四边形.
平行四边形的“中点四边形”是
.
平行四边形
矩形的“中点四边形”是
.
菱形
菱形的“中点四边形”是
.
矩形
正方形的“中点四边形”是
.
正方形
对角线互相垂直的四边形的“中点四边形”是
.
矩形
切换几何画板
对角线相等的四边形的“中点四边形”是
.
对角线相等且互相垂直的四边形的“中点四边形”是
.
菱形
正方形
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DE和中线AE互相平分.
分析:
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DF和中线AE互相平分.
证明:联结ED、EF.
∵D、E分别是AB、BC的中点,
∴DE∥AC(三角形的中位线平行于第三边).
同理:EF∥AB,
∴四边形DEFA是平行四边形(平行四边形的定义).
∴中位线DE和中线AE互相平分
(平行四边形的对角线互相平分).
适时小结:
已知两边中点构造三角形的中位线是
常用的添辅助线的方法之一.
通过本课的学习你有何收获?
课堂小结
1、三角形中位线的概念
在△ABC中,
∵
AD=BD,AE=CE,
∴
DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
2、三角形中位线定理
联结三角形两边的中点的线段叫做三角形的中位线.
布置作业
练习册
习题22.6(1)
§22.6三角形、梯形的中位线(1)
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
移动平行线,是否存在某个特殊
的位置,恰好使分割得的梯形和
三角形拼成一个平行四边形?
答:存在的,点E是AC的中点.
怎么拼?
答:若平行线与AB边交于点D,
将△AED绕点E旋转180°,
即得到□DBCD′.
切换几何画板
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
为什么拼出的图形是平行四边形?
图形的旋转
△ADE≌△CD′E
∠A=∠1
AB∥CD′
DE∥BC
四边形DBCD′是平行四边形
操作
如图,过△ABC边AC上的任意一点(除点A、C外),作BC
的平行线,可将三角形分割成一个三角形和一个梯形.
这时,点D位于线段AB的什么位置上?
答:由于CD′=DB
,且CD′=AD,所以AD=BD,点D是AB的中点.
点D、E分别是△ABC的边AB、AC的中点,
则线段DE是△ABC的一条特殊线段.
为什么拼出的图形是平行四边形?
三角形中位线的概念
联结三角形两边的中点的线段叫做三角形的中位线.
一个三角形共有几条中位线呢?
点D为AB中点,
点E为AC中点,
点F为BC中点,
则DF、FE、ED都是△ABC的中位线.
一个三角形共有三条中位线.
三角形的中位线与三角形的中线有何区别?
适时小结
三角形的中位线与三角形的中线的区别.
三角形
概念
图形
中位线
中线
联结两边中点的线段.
联结顶点与
其对边中点的线段.
两边中点
一顶点
一中点
学习三角形中位线定理
通过上述的操作过程,你能猜想△ABC的中位线DE与边BC有
怎样的位置关系和数量关系吗?
DE∥BC且
答:
猜想并归纳三角形中位线的性质.
如何证明你的猜想.
答:三角形的中位线平行于第三边,
并且等于第三边的一半.
如何证明四边形DBCF是平行四边形?
∴四边形BCFD是平行四边形
(一组对边平行且相等的四边形是平行四边形),
根据实验操作,如何添辅助线,构造与△ADE全等的三角形?
已知:如图,在△ABC中,AD=BD,AE=CE.
求证:DE∥BC,且
.
延长DE至点F,使EF=DE,联结CF.
证明:
∵AE=EC,∠2=∠3,
∴△ADE
≌△CFE,
∴AD=CF,∠A=∠1,
∴AB∥CF,即BD∥CF.
∵AD=BD,AD=CF,
∴DB=CF.
∴DF∥BC,且DF=BC.
∴DE∥BC,且
.
适时小结:
倍长中位线也是辅助线的常添方法之一.
学习三角形中位线定理
如何解决?
三角形中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
在△ABC中,
∵
AD=BD,AE=CE,
∴
DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
符号语言:
新知运用
(2)如果DE=5,那么BC=____.
10
(一)口答练习
1、如图,已知AD=DB,AE=EC,
(1)如果BC=
,那么DE=____;
新知运用
2、如图,B、C两点被海水隔开,在B、C外选择一点A,找到AB、AC的中点E、F,测量得EF=22米.这样就能求出B、C两点间的距离.请说出这是为什么?
答:∵
点E、F分别为AB、AC的中点,
∴
EF∥BC,且BC=2EF=44米
(三角形的中位线平行于第三边,
并且等于第三边的一半).
例题讲解
例题6
已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、
OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
由已知条件你能在图中找到什么?
GF、DE分别是△ABC和△OBC的中位线,且这两个三角形有公共边BC.
如何证明?
例题讲解
例题6
已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、
OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
证明:∵
点G、F分别为AB、AC的中点,
∴
GF∥BC,且
(三角形的中位线平行于第三边,
并且等于第三边的一半).
同理:DE∥BC,且
.
∴GF∥DE,且GF=DE.
∴四边形DEFG是平行四边形
(一组对边平行且相等的四边形是平行四边形).
变式2:顺次联结四边形四条边的中点,所得的四边形(称为“中点四边形”),是平行四边形吗?
分析:
例题讲解
例题6
已知:如图,点O是△ABC内任意一点,D、E、F、G分别是OB、
OC、AC、AB的中点.
求证:四边形DEFG是平行四边形.
变式1:如图,点O是△ABC外一点,以上结论是否还成立?
答:成立.
变
点O的位置
不变
GF、DE仍是△ABC和△OBC的中位线,且这两个三角形有公共边BC.
结论
四边形DEFG是平行四边形.
答:是的.
如何证明?
方法类似.
形变质不变
课堂练习
求证:顺次联结四边形四条边的中点,所得的四边形是平行四边形.
已知:如图,四边形ABCD中,
E、F、G、H分别是AB、BC、CD、DA的中点,
求证:四边形DEFG是平行四边形.
证明:联结BD.
适时小结
1、以上的三个问题图形变化,而本质是不变的.
2、任意四边形的“中点四边形”是平行四边形.
平行四边形的“中点四边形”是
.
平行四边形
矩形的“中点四边形”是
.
菱形
菱形的“中点四边形”是
.
矩形
正方形的“中点四边形”是
.
正方形
对角线互相垂直的四边形的“中点四边形”是
.
矩形
切换几何画板
对角线相等的四边形的“中点四边形”是
.
对角线相等且互相垂直的四边形的“中点四边形”是
.
菱形
正方形
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DE和中线AE互相平分.
分析:
课堂练习
已知:如图,△ABC中,D、E、F分别是AB、BC、CA三边的中点.
求证:中位线DF和中线AE互相平分.
证明:联结ED、EF.
∵D、E分别是AB、BC的中点,
∴DE∥AC(三角形的中位线平行于第三边).
同理:EF∥AB,
∴四边形DEFA是平行四边形(平行四边形的定义).
∴中位线DE和中线AE互相平分
(平行四边形的对角线互相平分).
适时小结:
已知两边中点构造三角形的中位线是
常用的添辅助线的方法之一.
通过本课的学习你有何收获?
课堂小结
1、三角形中位线的概念
在△ABC中,
∵
AD=BD,AE=CE,
∴
DE∥BC,且
(三角形的中位线平行于第三边,并且等于第三边的一半).
2、三角形中位线定理
联结三角形两边的中点的线段叫做三角形的中位线.
布置作业
练习册
习题22.6(1)
