沪教版(上海)数学八年级第二学期-22.1 探索多边形的内角和 课件(共25张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.1 探索多边形的内角和 课件(共25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 982.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
探索多边形的内角和
数学探究课
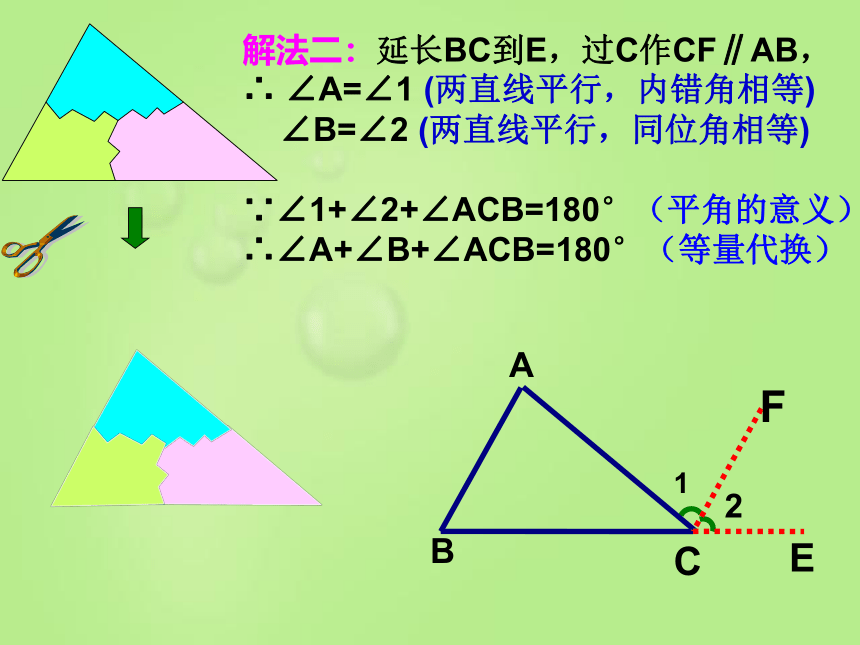
解法二:延长BC到E,过C作CF∥AB,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的意义)
∴∠A+∠B+∠ACB=180°(等量代换)
2
1
F
E
C
B
A
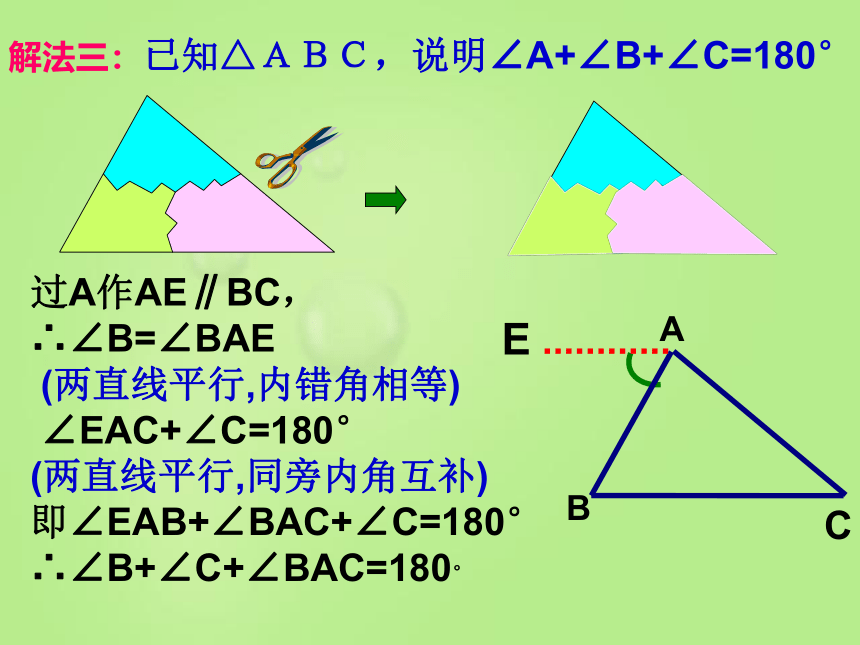
解法三:已知△ABC,说明∠A+∠B+∠C=180°
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAC+∠C=180°
(两直线平行,同旁内角互补)
即∠EAB+∠BAC+∠C=180°
∴∠B+∠C+∠BAC=180°
C
B
E
A
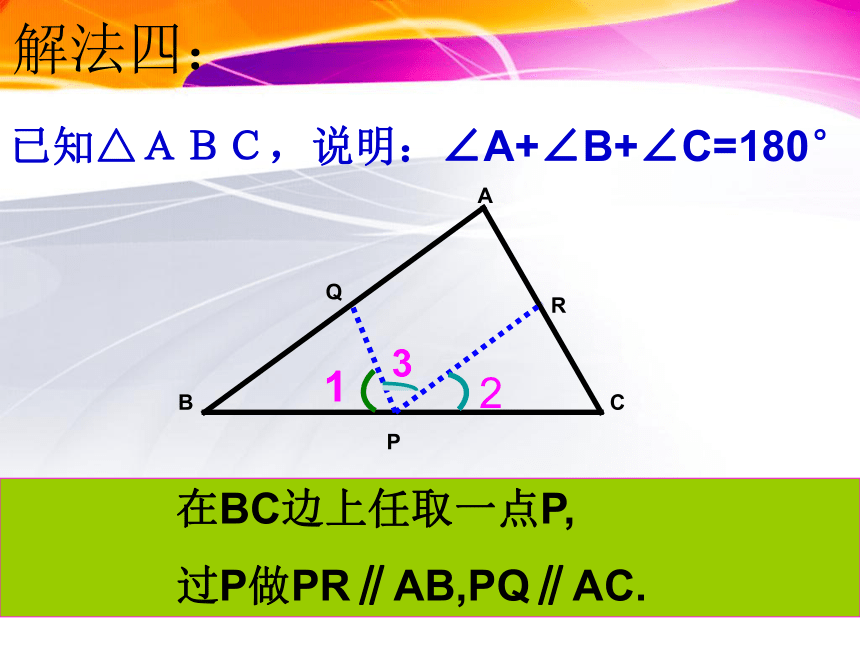
已知△ABC,说明:∠A+∠B+∠C=180°
解法四:
A
B
C
P
Q
R
1
2
3
在BC边上任取一点P,
过P做PR∥AB,PQ∥AC.
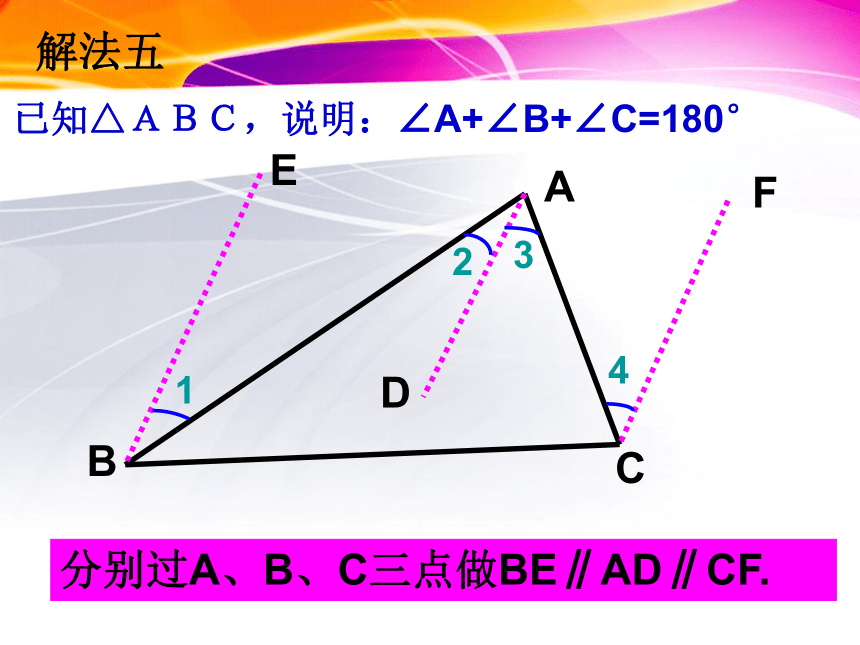
已知△ABC,说明:∠A+∠B+∠C=180°
A
B
C
D
E
F
1
2
3
4
解法五
分别过A、B、C三点做BE∥AD∥CF.
已知△ABC,说明:∠A+∠B+∠C=180°
A
B
C
E
F
D
Q
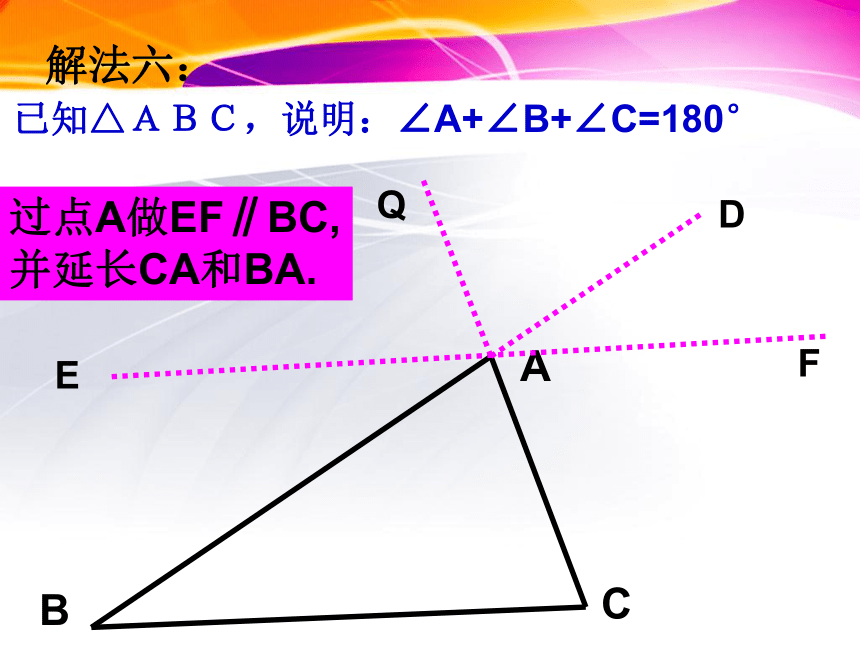
解法六:
过点A做EF∥BC,并延长CA和BA.
小亮同学探究三角形内角和经历了以下过程:
1、发现:他发现特殊三角形(一副三角尺)的三个特殊角的度数之和为180°
3、验证:
量一量:他任意画了一个三角形,量出三个角的度数,求得三个角的和为180°,验证了猜想.
拼一拼:他将三角形的三个内角剪下来拼在一起,恰好能拼成一个平角。再次验证了猜想。
2、猜想:任意三角形的三个内角之和为180°
4、证明:
他受拼图的启发,通过添加辅助线给出了三种证明方法,证明了:
三角形内角和为180°
找找身边的特殊四边形,
看看它们的内角和是多少?
常见的特殊四边形:
长方形
正方形
平行四边形
菱形
梯形
A
B
C
D
A
B
C
D
A
B
C
D
特殊四边形:长方形、正方形、平行四边形、菱形、梯形的内角和均为360°
(这里的凸四边形是指四个角均凸出来,没有凹进去的角)
发现:
猜想:
任意凸四边形的内角和为360°
量一量:
量一量你做好的四边形纸片的四个角的度数,看一看,它们的和是否为360°
验
证
猜
想
拼一拼:
将你做好的四边形纸片的四个角剪下来,四个角的顶点拼在一起,你会发现什么?
验
证
猜
想
四边形四个角的顶点拼在一起,正好拼成一个周角。验证了凸四边形的内角和为360°
证
明
猜
想:
解法一:如图,联结AC,四边形ABCD的内角和等于两个三角形内角和的和,
即:180°×2=360°。
A
B
D
C
凸四边形的内角和为360°
如图,说明:
∠A+
∠B+
∠C+
∠
D=360°
证
明
猜
想:
解法二:如图,联结AC、BD,四边形ABCD的内角和等于四个三角形内角和的和减去360°,即180°×4-360°=360°。
A
B
D
C
凸四边形的内角和为360°
证
明
猜
想:
解法三:如图,在四边形ABCD内取一点P,
联结PA、PB、PC、PD,四边形ABCD的内角和等于四个三角形内角和的和减去360°,
即180°×4-360°=360°。
A
B
D
C
P
凸四边形的内角和为360°
证
明
猜
想:
解法四:如图,在BC边上取一点P,联结PA、PD,四边形ABCD的内角和等于三个三角形内角和的和减去180°,即180°×3-180°=360°。
A
B
D
C
P
凸四边形的内角和为360°
证
明
猜
想:
解法五:如图,分别过点A、D做AE⊥BC
,
DF⊥BC,垂足分别为E、F,由三角形内角和为180°可得:∠BAE+∠B=90°,∠FDC+∠C=90°,由AE∥DF得:∠EAD+∠ADF=180°∴四边形ABCD的内角和=90°+90°+180°=360°.
A
B
D
C
凸四边形的内角和为360°
E
F
证
明
猜
想:
解法六:如图,联结AC,并延长至E,由三角形外角的性质,得:∠ECD=∠DAC+∠D,∠ECB=∠BAC+∠B,
∴四边形ABCD的内角和等于∠ECD+∠ECB+∠BCD=360°.
A
B
D
C
凸四边形的内角和为360°
E
证
明
猜
想:
解法七:如图,联结BD,延长BA至E,延长BC至F,∵∠EAD=∠ABD+∠BDA,∠FCD=∠CBD+∠BDC,∴四边形ABCD的内角和等于(∠EAD+∠BAD)+(∠FCD+∠BCD)=180°+180°=360°。
A
B
D
C
E
F
5边形
6边形
7边形
探索:多边形的内角和
对角线条数:
三角形个数:
内
角
和:
2
3
4
3
4
5
540°
720°
900°
…
n边形
?
?
?
过多边形的一个顶点做对角线
n-3
n-2
(n-2)
·180
n
边形的内角和公式:
(n-2)×180°
结论:
课堂小结:
通过本节课的学习,
谈谈你的收获、体会。
自主作业(选作)
1、探索n
边形的内角和的其它解法;
2、选一个多边形,列举求内角和的多种解法,写一篇小论文。
探索多边形的内角和
数学探究课
解法二:延长BC到E,过C作CF∥AB,
∴
∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°(平角的意义)
∴∠A+∠B+∠ACB=180°(等量代换)
2
1
F
E
C
B
A
解法三:已知△ABC,说明∠A+∠B+∠C=180°
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAC+∠C=180°
(两直线平行,同旁内角互补)
即∠EAB+∠BAC+∠C=180°
∴∠B+∠C+∠BAC=180°
C
B
E
A
已知△ABC,说明:∠A+∠B+∠C=180°
解法四:
A
B
C
P
Q
R
1
2
3
在BC边上任取一点P,
过P做PR∥AB,PQ∥AC.
已知△ABC,说明:∠A+∠B+∠C=180°
A
B
C
D
E
F
1
2
3
4
解法五
分别过A、B、C三点做BE∥AD∥CF.
已知△ABC,说明:∠A+∠B+∠C=180°
A
B
C
E
F
D
Q
解法六:
过点A做EF∥BC,并延长CA和BA.
小亮同学探究三角形内角和经历了以下过程:
1、发现:他发现特殊三角形(一副三角尺)的三个特殊角的度数之和为180°
3、验证:
量一量:他任意画了一个三角形,量出三个角的度数,求得三个角的和为180°,验证了猜想.
拼一拼:他将三角形的三个内角剪下来拼在一起,恰好能拼成一个平角。再次验证了猜想。
2、猜想:任意三角形的三个内角之和为180°
4、证明:
他受拼图的启发,通过添加辅助线给出了三种证明方法,证明了:
三角形内角和为180°
找找身边的特殊四边形,
看看它们的内角和是多少?
常见的特殊四边形:
长方形
正方形
平行四边形
菱形
梯形
A
B
C
D
A
B
C
D
A
B
C
D
特殊四边形:长方形、正方形、平行四边形、菱形、梯形的内角和均为360°
(这里的凸四边形是指四个角均凸出来,没有凹进去的角)
发现:
猜想:
任意凸四边形的内角和为360°
量一量:
量一量你做好的四边形纸片的四个角的度数,看一看,它们的和是否为360°
验
证
猜
想
拼一拼:
将你做好的四边形纸片的四个角剪下来,四个角的顶点拼在一起,你会发现什么?
验
证
猜
想
四边形四个角的顶点拼在一起,正好拼成一个周角。验证了凸四边形的内角和为360°
证
明
猜
想:
解法一:如图,联结AC,四边形ABCD的内角和等于两个三角形内角和的和,
即:180°×2=360°。
A
B
D
C
凸四边形的内角和为360°
如图,说明:
∠A+
∠B+
∠C+
∠
D=360°
证
明
猜
想:
解法二:如图,联结AC、BD,四边形ABCD的内角和等于四个三角形内角和的和减去360°,即180°×4-360°=360°。
A
B
D
C
凸四边形的内角和为360°
证
明
猜
想:
解法三:如图,在四边形ABCD内取一点P,
联结PA、PB、PC、PD,四边形ABCD的内角和等于四个三角形内角和的和减去360°,
即180°×4-360°=360°。
A
B
D
C
P
凸四边形的内角和为360°
证
明
猜
想:
解法四:如图,在BC边上取一点P,联结PA、PD,四边形ABCD的内角和等于三个三角形内角和的和减去180°,即180°×3-180°=360°。
A
B
D
C
P
凸四边形的内角和为360°
证
明
猜
想:
解法五:如图,分别过点A、D做AE⊥BC
,
DF⊥BC,垂足分别为E、F,由三角形内角和为180°可得:∠BAE+∠B=90°,∠FDC+∠C=90°,由AE∥DF得:∠EAD+∠ADF=180°∴四边形ABCD的内角和=90°+90°+180°=360°.
A
B
D
C
凸四边形的内角和为360°
E
F
证
明
猜
想:
解法六:如图,联结AC,并延长至E,由三角形外角的性质,得:∠ECD=∠DAC+∠D,∠ECB=∠BAC+∠B,
∴四边形ABCD的内角和等于∠ECD+∠ECB+∠BCD=360°.
A
B
D
C
凸四边形的内角和为360°
E
证
明
猜
想:
解法七:如图,联结BD,延长BA至E,延长BC至F,∵∠EAD=∠ABD+∠BDA,∠FCD=∠CBD+∠BDC,∴四边形ABCD的内角和等于(∠EAD+∠BAD)+(∠FCD+∠BCD)=180°+180°=360°。
A
B
D
C
E
F
5边形
6边形
7边形
探索:多边形的内角和
对角线条数:
三角形个数:
内
角
和:
2
3
4
3
4
5
540°
720°
900°
…
n边形
?
?
?
过多边形的一个顶点做对角线
n-3
n-2
(n-2)
·180
n
边形的内角和公式:
(n-2)×180°
结论:
课堂小结:
通过本节课的学习,
谈谈你的收获、体会。
自主作业(选作)
1、探索n
边形的内角和的其它解法;
2、选一个多边形,列举求内角和的多种解法,写一篇小论文。
