2020-2021学年北师大新版九年级下册数学第3章 圆单元测试卷(Word版有答案)
文档属性
| 名称 | 2020-2021学年北师大新版九年级下册数学第3章 圆单元测试卷(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 07:41:28 | ||
图片预览



文档简介
2020-2021学年北师大新版九年级下册数学《第3章
圆》单元测试卷
一.选择题
1.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A.
B.
C.
D.
2.以三角形的一边为直径的圆恰好与另一边相切,则此三角形是( )
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
3.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
4.如图,A是半径为2的⊙O外的一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则的长为( )
A.
B.
C.π
D.
5.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
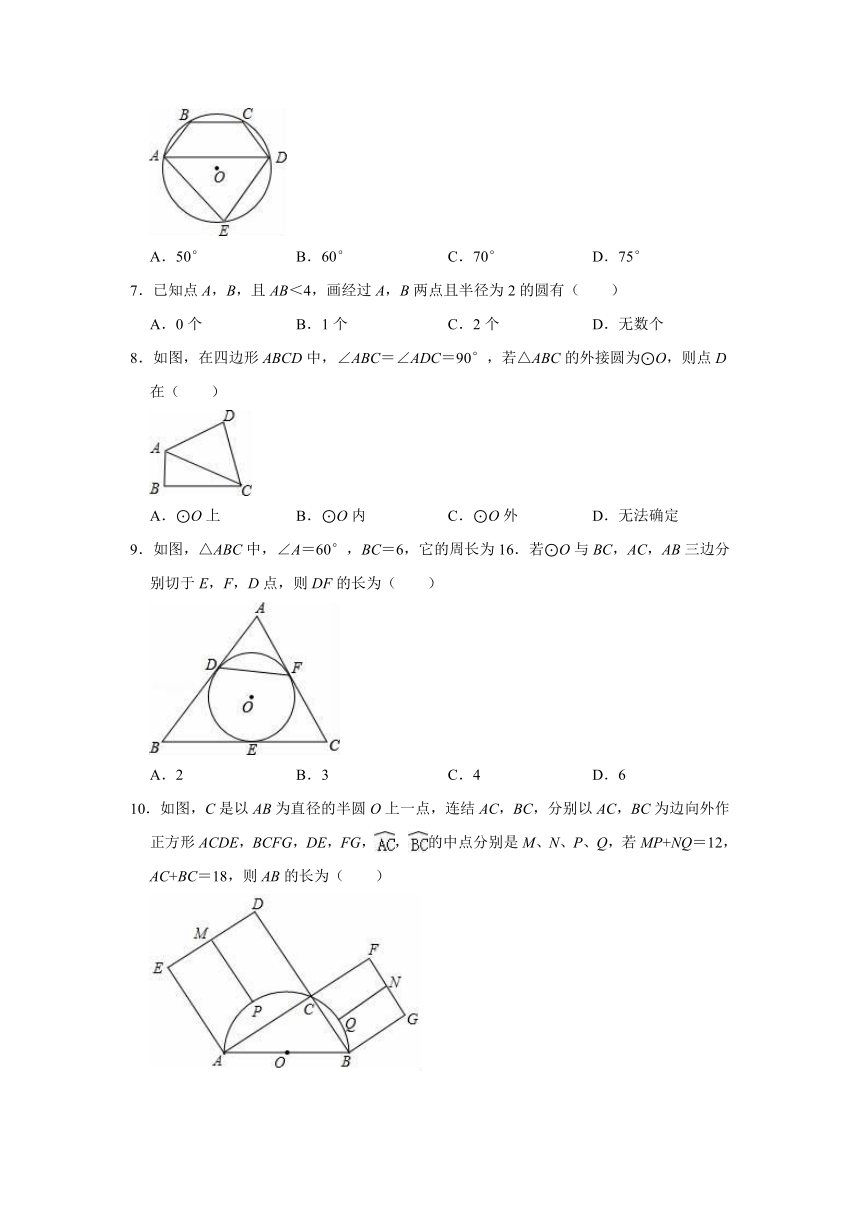
6.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于( )
A.50°
B.60°
C.70°
D.75°
7.已知点A,B,且AB<4,画经过A,B两点且半径为2的圆有( )
A.0个
B.1个
C.2个
D.无数个
8.如图,在四边形ABCD中,∠ABC=∠ADC=90°,若△ABC的外接圆为⊙O,则点D在( )
A.⊙O上
B.⊙O内
C.⊙O外
D.无法确定
9.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A.2
B.3
C.4
D.6
10.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M、N、P、Q,若MP+NQ=12,AC+BC=18,则AB的长为( )
A.9
B.
C.11
D.15
二.填空题
11.顶点在圆心的角叫做
角.
12.各边相等的圆内接多边形
正多边形;各角相等的圆内接多边形
正多边形.(填“是”或“不是”)
13.⊙O的半径为4,圆心O到直线l的距离是方程x2﹣7x+12=0的一个根,则直线l与⊙O的位置关系是
.
14.以等腰三角形顶角的顶点为圆心,顶角的平分线为半径的圆必与
相切.
15.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A和点B有且只有一个点在⊙D内,则x的取值范围是
.
16.如图,AC、BD为⊙O的两条弦,且AC⊥BD,⊙O的半径为,则AB2+CD2的值为
.
17.在同圆或等圆中,同弧或等弧所对圆周角
,相等的圆周角所对的弧
,同弧或等弧所对圆周角是其所对的圆心角的
.
18.扇形面积计算:
方法一:如果已知扇形圆心角为n,半径为r,那么扇形面积s=
;
方法二:如果已知扇形弧长为l,半径为r,那么扇形面积s=
.
19.如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中,,,,,,…的圆心依次按点A、B、C、D、E、F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2011=
.
20.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为
,最大值为
.
三.解答题
21.如图,在图中,用图形(阴影)表示与A的距离小于或等于2cm的所有点组成的图形.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
23.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,求阴影部分的面积.
24.如图,AB是⊙O的直径.
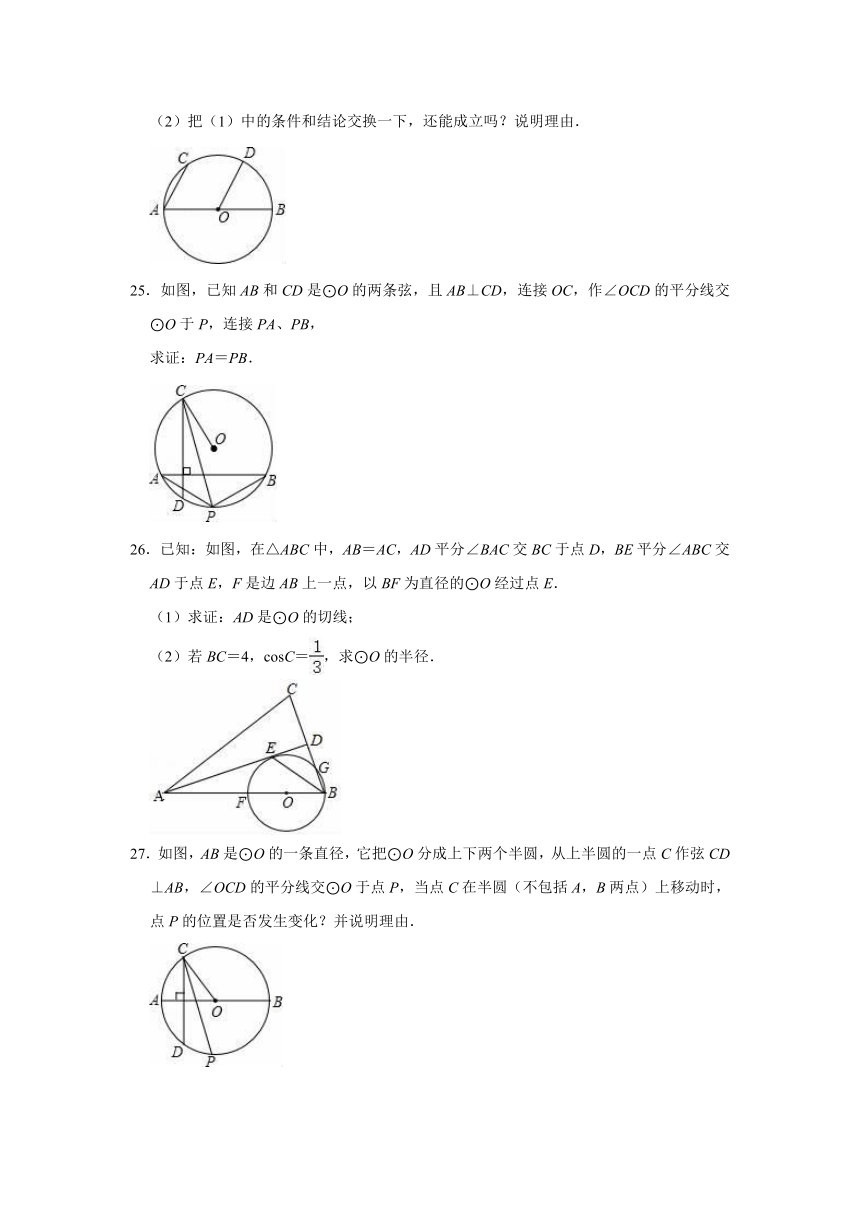
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
25.如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
求证:PA=PB.
26.已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E,F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC=,求⊙O的半径.
27.如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
参考答案与试题解析
一.选择题
1.解:.
故选:C.
2.解:如图所示,
∵AB是直径,AC是切线,
∴AB⊥AC,
∴△ABC是直角三角形.
故选:B.
3.解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
B、假命题,因为任何多边形的外角和均为360°,则其每个外角为α=,可见,当n增大时,α减小;
C、真命题,因为菱形的对角线是其对称轴,两条对角线的交点是对称中心;
D、假命题,因为两直线平行,同旁内角互补.
故选:C.
4.解:如图:连接OC、OB,
在Rt△OAB中,OA=4,OB=2,
故∠OAB=30°,∠AOB=∠3=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴∠4=60°,
==.
故选:A.
5.解:C=π×8=8π,
2C=16π,
2006π=16π×125+6π,
所以停止在D点.
故选:A.
6.解:连接OA,OB,OC,OD,
∵∠BAD=50°,==,
∴∠BOD=2∠BAD=100°,
∵==,
∴AOB=∠BOC=∠COD=∠BOD=50°,
∴∠AOD=∠AOB+∠BOC+∠COD=150°,
∴∠AED=∠AOD=75°.
故选:D.
7.解:根据题意作图如右,
由图可知经过A,B两点且半径为2的圆有2个.
故选:C.
8.解:∵∠ABC=90°,
∴AC是△ABC的外接圆⊙O的直径,
而∠ADC=90°,
∴点D在⊙O上,
所以A对,B,C,D都错.故选A.
9.解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,
∴AD=AF,BE=BD,CE=CF,
∵BC=BE+CE=6,
∴BD+CF=6,
∵AD=AF,∠A=60°,
∴△ADF是等边三角形,
∴AD=AF=DF,
∵AB+AC+BC=16,BC=6,
∴AB+AC=10,
∵BD+CF=6,
∴AD+AF=4,
∵AD=AF=DF,
∴DF=AF=AD=×4=2,
故选:A.
10.解:连接OP,OQ,
∵DE,FG,,的中点分别是M,N,P,Q,
∴OP⊥AC,OQ⊥BC,
∴H、I是AC、BD的中点,
∴OH+OI=(AC+BC)=9,
∵MH+NI=AC+BC=18,MP+NQ=12,
∴PH+QI=18﹣12=6,
∴AB=OP+OQ=OH+OI+PH+QI=9+6=15,
故选:D.
二.填空题
11.解;∵圆心角的概念为:顶点在圆心的角
∴答案为圆心角.
12.解:∵正多边形的各边相等,
∴各边所对的圆周角必然相等,
∴各边相等的圆内接多边形是正多边形;
∵圆内接多边形的各角相等;
举出一个反例:当四个角都是直角时,这个四边形可能是矩形,
∴各角相等的圆内接多边形不一定是正多边形.
故答案为:是,不是.
13.解:∵x2﹣7x+12=0,
∴(x﹣3)(x﹣4)=0,
解得:x1=3,x2=4,
∵点O到直线l距离是方程x2﹣7x+12=0的一个根,即为3或4,
∴点O到直线l的距离d=3或4,r=4,
∴d=r或d<r
∴直线l与圆相交或相切.
故答案为:相交或相切.
14.解:根据等腰三角形的性质可得等腰三角形顶角平分线,底边的中线以及底边上的高重合,以及切线的判定(经过半径的外端且垂直于这条半径的直线是圆的切线)可得到以等腰三角形顶角的顶点为圆心,顶角的平分线为半径的圆必与底边相切.
15.解:连接DB,如图,
∵四边形ABCD为矩形,
∴∠A=90°,
∴BD==5,
∵点A和点B有且只有一个点在⊙D内,
∴点A在圆⊙D内,点D在圆⊙D上或圆⊙D外,
∴3<x≤5.
故答案为3<x≤5.
16.解:作直径AE,连结CE、BE,如图,
∵AE为直径,
∴∠ACE=90°,即CE⊥AC,∠ABE=90°,
∵AC⊥BD,
∴BD∥CE,
∴BE弧=DC弧,
∴BE=CD,
在Rt△ABE中,AB2+BE2=AE2=12=1,
∴AB2+CD2=1.
故答案为1.
17.解:由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角
相等,
相等的圆周角所对的弧
相等,
同弧或等弧所对圆周角是其所对的圆心角的一半.
故答案为:相等、相等、一半.
18.解:若已知扇形圆心角为n,半径为r,S扇形面积=;
若已知扇形弧长为l,半径为r,S扇形面积==××R=lr;
故答案为;
lr;
19.解:L1==;
L2==;
L3==;
L4==;
按照这种规律可以得到:
Ln=,
∴L2011=.
故答案为:.
20.解:如图所示,
过O作OM′⊥AB,连接OA,
∵过直线外一点与直线上的所有连线中垂线段最短,
∴当OM于OM′重合时OM最短,
∵AB=8,OA=5,
∴AM′=×8=4,
∴在Rt△OAM′中,OM′===3,
∴线段OM长的最小值为3,最大值为5.
故答案为:3,5.
三.解答题
21.
解:如图,与A的距离小于或等于2cm的所有点组成的图形是如图所示的阴影部分.
22.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
23.解:连接OB,OC,
∵AB是圆的切线,
∴∠ABO=90°,
在直角△ABO中,OB=2,OA=4,
∴∠OAB=30°,∠AOB=60°,
∵OA∥BC,
∴∠CBO=∠AOB=60°,且S阴影部分=S扇形△BOC,
∴△BOC是等边三角形,边长是2,
∴S阴影部分=S扇形△BOC==,即图中阴影部分的面积是.
24.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
25.证明:∵OC=OP,
∴∠1=∠2.
∵CP平分∠OCD,
∴∠2=∠3,
∴∠3=∠1,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB.
∴=,
∴PA=PB.
26.(1)证明:连接OE,如图所示:
则OE=OB,
∴∠OEB=∠OBE,
∵BE平分∠ABC,
∴∠0BE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠ADB,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
∴∠AEO=90°,
∴OE⊥AD,
∴AD与⊙O相切;
(2)解:∵AB=AC,AD平分∠BAC,
∴BD=BC,∠ABC=∠C,
∵BC=4,cosC=,
∴BD=2,cos∠ABC=,
在Rt△ABD中,AB==6,
设⊙O的半径为r,则OA=6﹣r,
∵OE∥BC,
∴△AOE∽△ABD,
∴,
即,
解得:r=,
∴⊙O的半径为.
27.解:不发生变化.
连接OP,
∵OP=OC,
∴∠P=∠OCP,
∵∠OCP=∠DCP,
∴∠P=∠DCP,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB,
∴=,
∴点P为的中点不变.
圆》单元测试卷
一.选择题
1.在一扇形统计图中,有一扇形的圆心角为60°,则此扇形占整个圆的( )
A.
B.
C.
D.
2.以三角形的一边为直径的圆恰好与另一边相切,则此三角形是( )
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
3.下列命题中真命题是( )
A.两个等腰三角形一定全等
B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形
D.两直线平行,同旁内角相等
4.如图,A是半径为2的⊙O外的一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则的长为( )
A.
B.
C.π
D.
5.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
6.如图,==,AD为⊙O的弦,∠BAD=50°,则∠AED等于( )
A.50°
B.60°
C.70°
D.75°
7.已知点A,B,且AB<4,画经过A,B两点且半径为2的圆有( )
A.0个
B.1个
C.2个
D.无数个
8.如图,在四边形ABCD中,∠ABC=∠ADC=90°,若△ABC的外接圆为⊙O,则点D在( )
A.⊙O上
B.⊙O内
C.⊙O外
D.无法确定
9.如图,△ABC中,∠A=60°,BC=6,它的周长为16.若⊙O与BC,AC,AB三边分别切于E,F,D点,则DF的长为( )
A.2
B.3
C.4
D.6
10.如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG,,的中点分别是M、N、P、Q,若MP+NQ=12,AC+BC=18,则AB的长为( )
A.9
B.
C.11
D.15
二.填空题
11.顶点在圆心的角叫做
角.
12.各边相等的圆内接多边形
正多边形;各角相等的圆内接多边形
正多边形.(填“是”或“不是”)
13.⊙O的半径为4,圆心O到直线l的距离是方程x2﹣7x+12=0的一个根,则直线l与⊙O的位置关系是
.
14.以等腰三角形顶角的顶点为圆心,顶角的平分线为半径的圆必与
相切.
15.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为x的圆,使点A和点B有且只有一个点在⊙D内,则x的取值范围是
.
16.如图,AC、BD为⊙O的两条弦,且AC⊥BD,⊙O的半径为,则AB2+CD2的值为
.
17.在同圆或等圆中,同弧或等弧所对圆周角
,相等的圆周角所对的弧
,同弧或等弧所对圆周角是其所对的圆心角的
.
18.扇形面积计算:
方法一:如果已知扇形圆心角为n,半径为r,那么扇形面积s=
;
方法二:如果已知扇形弧长为l,半径为r,那么扇形面积s=
.
19.如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中,,,,,,…的圆心依次按点A、B、C、D、E、F循环,其弧长分别记为l1,l2,l3,l4,l5,l6,….当AB=1时,l2011=
.
20.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为
,最大值为
.
三.解答题
21.如图,在图中,用图形(阴影)表示与A的距离小于或等于2cm的所有点组成的图形.
22.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当BC=CE=2时,求DE的长度.
23.如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,B为切点,弦BC∥OA,连接AC,求阴影部分的面积.
24.如图,AB是⊙O的直径.
(1)若OD∥AC,与的大小有什么关系?为什么?
(2)把(1)中的条件和结论交换一下,还能成立吗?说明理由.
25.如图,已知AB和CD是⊙O的两条弦,且AB⊥CD,连接OC,作∠OCD的平分线交⊙O于P,连接PA、PB,
求证:PA=PB.
26.已知:如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,BE平分∠ABC交AD于点E,F是边AB上一点,以BF为直径的⊙O经过点E.
(1)求证:AD是⊙O的切线;
(2)若BC=4,cosC=,求⊙O的半径.
27.如图,AB是⊙O的一条直径,它把⊙O分成上下两个半圆,从上半圆的一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在半圆(不包括A,B两点)上移动时,点P的位置是否发生变化?并说明理由.
参考答案与试题解析
一.选择题
1.解:.
故选:C.
2.解:如图所示,
∵AB是直径,AC是切线,
∴AB⊥AC,
∴△ABC是直角三角形.
故选:B.
3.解:A、假命题,因为如图所示:AD=AE,AB=AC,但△ADE与△ABC不全等;
B、假命题,因为任何多边形的外角和均为360°,则其每个外角为α=,可见,当n增大时,α减小;
C、真命题,因为菱形的对角线是其对称轴,两条对角线的交点是对称中心;
D、假命题,因为两直线平行,同旁内角互补.
故选:C.
4.解:如图:连接OC、OB,
在Rt△OAB中,OA=4,OB=2,
故∠OAB=30°,∠AOB=∠3=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴∠4=60°,
==.
故选:A.
5.解:C=π×8=8π,
2C=16π,
2006π=16π×125+6π,
所以停止在D点.
故选:A.
6.解:连接OA,OB,OC,OD,
∵∠BAD=50°,==,
∴∠BOD=2∠BAD=100°,
∵==,
∴AOB=∠BOC=∠COD=∠BOD=50°,
∴∠AOD=∠AOB+∠BOC+∠COD=150°,
∴∠AED=∠AOD=75°.
故选:D.
7.解:根据题意作图如右,
由图可知经过A,B两点且半径为2的圆有2个.
故选:C.
8.解:∵∠ABC=90°,
∴AC是△ABC的外接圆⊙O的直径,
而∠ADC=90°,
∴点D在⊙O上,
所以A对,B,C,D都错.故选A.
9.解:∵⊙O与BC,AC,AB三边分别切于E,F,D点,
∴AD=AF,BE=BD,CE=CF,
∵BC=BE+CE=6,
∴BD+CF=6,
∵AD=AF,∠A=60°,
∴△ADF是等边三角形,
∴AD=AF=DF,
∵AB+AC+BC=16,BC=6,
∴AB+AC=10,
∵BD+CF=6,
∴AD+AF=4,
∵AD=AF=DF,
∴DF=AF=AD=×4=2,
故选:A.
10.解:连接OP,OQ,
∵DE,FG,,的中点分别是M,N,P,Q,
∴OP⊥AC,OQ⊥BC,
∴H、I是AC、BD的中点,
∴OH+OI=(AC+BC)=9,
∵MH+NI=AC+BC=18,MP+NQ=12,
∴PH+QI=18﹣12=6,
∴AB=OP+OQ=OH+OI+PH+QI=9+6=15,
故选:D.
二.填空题
11.解;∵圆心角的概念为:顶点在圆心的角
∴答案为圆心角.
12.解:∵正多边形的各边相等,
∴各边所对的圆周角必然相等,
∴各边相等的圆内接多边形是正多边形;
∵圆内接多边形的各角相等;
举出一个反例:当四个角都是直角时,这个四边形可能是矩形,
∴各角相等的圆内接多边形不一定是正多边形.
故答案为:是,不是.
13.解:∵x2﹣7x+12=0,
∴(x﹣3)(x﹣4)=0,
解得:x1=3,x2=4,
∵点O到直线l距离是方程x2﹣7x+12=0的一个根,即为3或4,
∴点O到直线l的距离d=3或4,r=4,
∴d=r或d<r
∴直线l与圆相交或相切.
故答案为:相交或相切.
14.解:根据等腰三角形的性质可得等腰三角形顶角平分线,底边的中线以及底边上的高重合,以及切线的判定(经过半径的外端且垂直于这条半径的直线是圆的切线)可得到以等腰三角形顶角的顶点为圆心,顶角的平分线为半径的圆必与底边相切.
15.解:连接DB,如图,
∵四边形ABCD为矩形,
∴∠A=90°,
∴BD==5,
∵点A和点B有且只有一个点在⊙D内,
∴点A在圆⊙D内,点D在圆⊙D上或圆⊙D外,
∴3<x≤5.
故答案为3<x≤5.
16.解:作直径AE,连结CE、BE,如图,
∵AE为直径,
∴∠ACE=90°,即CE⊥AC,∠ABE=90°,
∵AC⊥BD,
∴BD∥CE,
∴BE弧=DC弧,
∴BE=CD,
在Rt△ABE中,AB2+BE2=AE2=12=1,
∴AB2+CD2=1.
故答案为1.
17.解:由圆心角、弧、弦的关系及圆周角定理可知:在同圆或等圆中,同弧或等弧所对圆周角
相等,
相等的圆周角所对的弧
相等,
同弧或等弧所对圆周角是其所对的圆心角的一半.
故答案为:相等、相等、一半.
18.解:若已知扇形圆心角为n,半径为r,S扇形面积=;
若已知扇形弧长为l,半径为r,S扇形面积==××R=lr;
故答案为;
lr;
19.解:L1==;
L2==;
L3==;
L4==;
按照这种规律可以得到:
Ln=,
∴L2011=.
故答案为:.
20.解:如图所示,
过O作OM′⊥AB,连接OA,
∵过直线外一点与直线上的所有连线中垂线段最短,
∴当OM于OM′重合时OM最短,
∵AB=8,OA=5,
∴AM′=×8=4,
∴在Rt△OAM′中,OM′===3,
∴线段OM长的最小值为3,最大值为5.
故答案为:3,5.
三.解答题
21.
解:如图,与A的距离小于或等于2cm的所有点组成的图形是如图所示的阴影部分.
22.(1)证明:∵OD⊥AC,
∴=,
∴∠ABD=∠CBD,
∴BD平分∠ABC;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD⊥AC,
∴AE=CE=2,
在Rt△ABC中,AB==2,
∴OD=,
∵AE=CE,OA=OB,
∴OE为△ABC的中位线,
∴OE=BC=1,
∴DE=﹣1.
23.解:连接OB,OC,
∵AB是圆的切线,
∴∠ABO=90°,
在直角△ABO中,OB=2,OA=4,
∴∠OAB=30°,∠AOB=60°,
∵OA∥BC,
∴∠CBO=∠AOB=60°,且S阴影部分=S扇形△BOC,
∴△BOC是等边三角形,边长是2,
∴S阴影部分=S扇形△BOC==,即图中阴影部分的面积是.
24.解:(1).
证明:延长DO交⊙O于E,
∵AC∥OD
∴
∵∠1=∠2
∴
∴;
(2)仍成立.
证明:延长DO交⊙O于点E,连接AD,
∵,
∴
∴∠3=∠D
∴AC∥OD.
25.证明:∵OC=OP,
∴∠1=∠2.
∵CP平分∠OCD,
∴∠2=∠3,
∴∠3=∠1,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB.
∴=,
∴PA=PB.
26.(1)证明:连接OE,如图所示:
则OE=OB,
∴∠OEB=∠OBE,
∵BE平分∠ABC,
∴∠0BE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
∴∠AEO=∠ADB,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADB=90°,
∴∠AEO=90°,
∴OE⊥AD,
∴AD与⊙O相切;
(2)解:∵AB=AC,AD平分∠BAC,
∴BD=BC,∠ABC=∠C,
∵BC=4,cosC=,
∴BD=2,cos∠ABC=,
在Rt△ABD中,AB==6,
设⊙O的半径为r,则OA=6﹣r,
∵OE∥BC,
∴△AOE∽△ABD,
∴,
即,
解得:r=,
∴⊙O的半径为.
27.解:不发生变化.
连接OP,
∵OP=OC,
∴∠P=∠OCP,
∵∠OCP=∠DCP,
∴∠P=∠DCP,
∴CD∥OP,
∵CD⊥AB,
∴OP⊥AB,
∴=,
∴点P为的中点不变.
