沪教版(上海)数学八年级第二学期-21.7 分式方程的应用复习 课件(共15张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-21.7 分式方程的应用复习 课件(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 21:15:53 | ||
图片预览






文档简介
(共15张PPT)
分式方程的应用复习
想一想
解分式方程一般需要经过哪几个步骤?
2、解这个整式方程
4、得出结论,写答句
3、检验
解:
方程两边同乘以x-2,
得
1-x=-1-2(x-2)
解这个方程,得
x=2
检验:
把X=2代入最简公分母
X-2=2-2=0
所以,X=2是增根,舍去
原方程无解
1、去分母,化成整式方程
步骤:
列方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
复习回忆
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
各种问题的量与量关系:
工程问题:
工作效率×工作时间=工作总量
行程问题:
速度
×
时间
=
路程
价格问题:
单价
×
份数
=
总价
顺逆流问题:
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
顺逆风问题:
顺风速度=自身速度+风速
逆风速度=自身速度-风速
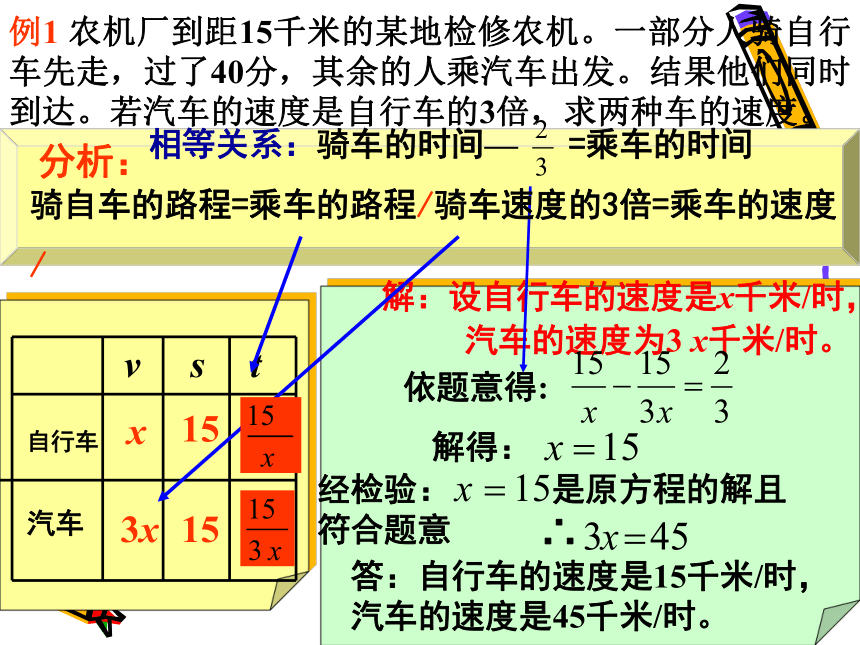
例1
农机厂到距15千米的某地检修农机。一部分人骑自行车先走,过了40分,其余的人乘汽车出发。结果他们同时到达。若汽车的速度是自行车的3倍,求两种车的速度。
自行车
汽车
v
s
t
解:设自行车的速度是x千米/时,
汽车的速度为3
x千米/时。
依题意得:
解得:
经检验:
是原方程的解且符合题意
∴
答:自行车的速度是15千米/时,
汽车的速度是45千米/时。
15
15
x
3x
相等关系:骑车的时间—
=乘车的时间
骑自车的路程=乘车的路程/骑车速度的3倍=乘车的速度
/
分析:
小民和小强到校办工厂实习,两人各要做某种零件15个,小民先做,过了40分钟,小强才开始做,由于小强技术熟练,结果他们同时做完。已知小强每小时做零件的个数是小民的3倍,求小强、小民每小时各做多少个?
问题2--变式练习:
解:设甲每小时做x个,则乙每小时做3x个,
依题意得:
分析:这是一个工作量的问题
问题4:我部队到某桥头阻击敌人,出发时敌军离桥头24Km,我部队离桥头30Km,我部队急行军速度比敌军的速度快2.5
千米/时,结果比敌人提前48分钟到达,求我部队急行军的速度。
等量关系:
我军的时间=
敌军的时间
解:设敌军的速度为X千米/时,则我军为(X+2.5)千米/时。
由题意得方程:
路程
速度
时间
敌军
我军
24
30
x
X+2.5
24/x
30/(x+2.5)
?
–
设敌军的速度为X千米/时
桥
敌军
我军
24Km
30Km
24Km
30Km
例:一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
解:设江水的流速为
v
千米/时,根据题意,得
情
境
问
题
甲、乙两个建筑队完成某项工程,若两队同时开工,12天就可以完成工程;乙队单独完成该工程比甲队单独完成该工程多用10天.问单独完成此项工程,乙队需要多少天?
分析:
(1)设乙单独完成工程需x天,则甲单独完成工程需(
)天;
(2)甲做1天的工作量+乙做1天的工作量=甲、乙两人合做1天的工作量;
例题分析:
解:
设乙单独完成工程需x天,则甲单独完成工程需(
)天;
解这个方程:得x
1=30,x
2=4;
经检验,x
1=30,x
2=4都是原方程的根,当x=30时,x-10=20,当x=4时,x-10=-6,因为时间不能为负数,所以只能取x=30;
答:乙队单独完成此项工程需要30天.
根据题意得:
课堂练习:
1、A做90个零件所需要的时间和B做120个零件所用的时间相同,又知每小时A、B两人共做35个机器零件。求A、B每小时各做多少个零件。
2、从甲站到乙站有150千米,一列快车与一列慢车同时从甲站开出,1小时后快车在慢车前面12千米;快车到达乙站比慢车早25分钟。快车与慢车每小时各走多少千米?
做一做:
3、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
列分式方程解应用题的方法与步骤为:
1
审
——审清题意
2
设
——直接设未知数,
或间接设未知数
3
列
——根据等量关系列出分式方程
——解这个分式方程
5
验
——既要验是否为所列分式方程的根,
又要验是否符合实际情况
——完整地写出答案,注意单位
小结:
4
解
6
答
作
业
布
置
练习卷
再
见
分式方程的应用复习
想一想
解分式方程一般需要经过哪几个步骤?
2、解这个整式方程
4、得出结论,写答句
3、检验
解:
方程两边同乘以x-2,
得
1-x=-1-2(x-2)
解这个方程,得
x=2
检验:
把X=2代入最简公分母
X-2=2-2=0
所以,X=2是增根,舍去
原方程无解
1、去分母,化成整式方程
步骤:
列方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
复习回忆
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
各种问题的量与量关系:
工程问题:
工作效率×工作时间=工作总量
行程问题:
速度
×
时间
=
路程
价格问题:
单价
×
份数
=
总价
顺逆流问题:
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
顺逆风问题:
顺风速度=自身速度+风速
逆风速度=自身速度-风速
例1
农机厂到距15千米的某地检修农机。一部分人骑自行车先走,过了40分,其余的人乘汽车出发。结果他们同时到达。若汽车的速度是自行车的3倍,求两种车的速度。
自行车
汽车
v
s
t
解:设自行车的速度是x千米/时,
汽车的速度为3
x千米/时。
依题意得:
解得:
经检验:
是原方程的解且符合题意
∴
答:自行车的速度是15千米/时,
汽车的速度是45千米/时。
15
15
x
3x
相等关系:骑车的时间—
=乘车的时间
骑自车的路程=乘车的路程/骑车速度的3倍=乘车的速度
/
分析:
小民和小强到校办工厂实习,两人各要做某种零件15个,小民先做,过了40分钟,小强才开始做,由于小强技术熟练,结果他们同时做完。已知小强每小时做零件的个数是小民的3倍,求小强、小民每小时各做多少个?
问题2--变式练习:
解:设甲每小时做x个,则乙每小时做3x个,
依题意得:
分析:这是一个工作量的问题
问题4:我部队到某桥头阻击敌人,出发时敌军离桥头24Km,我部队离桥头30Km,我部队急行军速度比敌军的速度快2.5
千米/时,结果比敌人提前48分钟到达,求我部队急行军的速度。
等量关系:
我军的时间=
敌军的时间
解:设敌军的速度为X千米/时,则我军为(X+2.5)千米/时。
由题意得方程:
路程
速度
时间
敌军
我军
24
30
x
X+2.5
24/x
30/(x+2.5)
?
–
设敌军的速度为X千米/时
桥
敌军
我军
24Km
30Km
24Km
30Km
例:一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
解:设江水的流速为
v
千米/时,根据题意,得
情
境
问
题
甲、乙两个建筑队完成某项工程,若两队同时开工,12天就可以完成工程;乙队单独完成该工程比甲队单独完成该工程多用10天.问单独完成此项工程,乙队需要多少天?
分析:
(1)设乙单独完成工程需x天,则甲单独完成工程需(
)天;
(2)甲做1天的工作量+乙做1天的工作量=甲、乙两人合做1天的工作量;
例题分析:
解:
设乙单独完成工程需x天,则甲单独完成工程需(
)天;
解这个方程:得x
1=30,x
2=4;
经检验,x
1=30,x
2=4都是原方程的根,当x=30时,x-10=20,当x=4时,x-10=-6,因为时间不能为负数,所以只能取x=30;
答:乙队单独完成此项工程需要30天.
根据题意得:
课堂练习:
1、A做90个零件所需要的时间和B做120个零件所用的时间相同,又知每小时A、B两人共做35个机器零件。求A、B每小时各做多少个零件。
2、从甲站到乙站有150千米,一列快车与一列慢车同时从甲站开出,1小时后快车在慢车前面12千米;快车到达乙站比慢车早25分钟。快车与慢车每小时各走多少千米?
做一做:
3、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
列分式方程解应用题的方法与步骤为:
1
审
——审清题意
2
设
——直接设未知数,
或间接设未知数
3
列
——根据等量关系列出分式方程
——解这个分式方程
5
验
——既要验是否为所列分式方程的根,
又要验是否符合实际情况
——完整地写出答案,注意单位
小结:
4
解
6
答
作
业
布
置
练习卷
再
见
