沪教版(上海)数学八年级第二学期-21.6 代数方程复习(二) 课件(共27张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-21.6 代数方程复习(二) 课件(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
代数方程复习(二)
分式方程、无理方程、二元二次方程组
分式方程:
分母中含有未知数的有理方程。
无理方程:
根号内含有未知数的方程。
相关概念
二元二次
方程组:
方程组中含有两个未知数,并且含有未知数的项的最高次数为两次,这样的整式方程组叫做二元二次方程组.
1.下列方程中,不是分式方程的是(
)
A
B
C
D
看分母中有没有未知数。
D
练习
2.方程
的解是(
)
A
B
C
D
D
除了使方程左右两边相等外,在分式方程中,首先必须使分式有意义.
3、下列方程有实数根的是(
)
A
4、若关于x的方程
无实数根,则m的取值范围是(
)
(A)大于零
(B)小于零
(C)不大于零
(D)不小于零
B
5、下列方程组中,属于二元二次方程组的是(
)
C
A
B
C
D
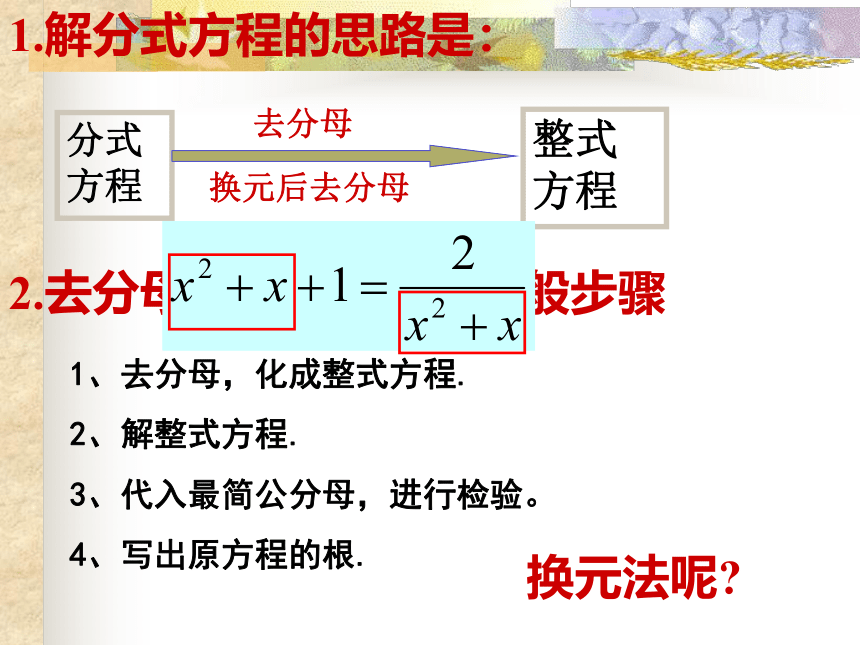
2.去分母解分式方程的一般步骤
1、去分母,化成整式方程.
2、解整式方程.
3、代入最简公分母,进行检验。
4、写出原方程的根.
1.解分式方程的思路是:
分式方程
整式方程
去分母
换元后去分母
换元法呢?
例题:
1、解方程:
例题:
解:设x2+x=y,则原方程可化为
y2+y-2=0
去分母并整理得
y1=-2,
y2=1
解得
当y1=-2时,
x2+x=-2,
△<0,无实数根
当y2=1时,
x2+x=1,解得
经检验
是原方程的根.
∴原方程的根是
练习:
_________
3
2
5
)
2
(
_________
1
1
5
)
1
(
的解是
分式方程
的解为
分式方程
x
x
x
=
-
=
+
x=4
x=-3
原方程可化为整式方程:_____________
x+2
x-2
———
-
16
x2-4
———
=
1
x+2
———
(3)
x2+3x-10=0
3x
x2-1
———
+
x2-1
x
———
=
7
2
——
(4)
设_______=y,则原方程可化为
关于y的整式方程为__________
x2-1
———
x
6y2-7y+2=0
练习:
(5)用换元法解方程:
(5)用换元法解方程:
∴y2+y-6=0,即(y+3)(y-2)=0,
y1=-3,y2=2
当y=-3时,x2-x=-3,△<0,无实数根
当y=2时,原方程为x2-x-2=0,x1=2,x2=-1.
经检验x1=2,x2=-1是原方程的根.
∴原方程的根是
x1=2,x2=-1
2.解无理方程的一般步骤
1、通过两边同平方去掉根号,转化为有理方程。
2、解有理方程.
3、代入原方程进行检验。
4、写出原方程的根.
1.解无理方程的思路是:
无理方程
有理方程
平方
例题:
(2)
解方程
x=5
x=0
x1=-5,
x2=1
无实数根
X=20
1.解二元二次方程组的方法是:
(1)代入法:将一个未知数用另一个未知数表示,代入第二个方程,解一元二次方程,然后将求得的未知数的值代回两元一次方程中,求另一个未知数的值,最后写出方程组的解。
(2)因式分解法:将其中一个二元二次方程因式分解成两个一次方程,分别与另一个方程组成方程组,再解方程组。
(1)
x-3y=0
x2+y=20
(2)
x2-3xy+2y2=0
x2+y2=5
本题宜采用_________法
代入消元
本题宜采用__________法
因式分解
解方程组:
消元后的方程为______________
9y2+y-20=0
原方程组可化为以下两个方程组:
x-y=0
x2+y2
=5
x-2y=0
x2+y2
=5
练习:
(3)
(4)
错在哪里?
(1)解关于x的方程:
bx2+1=2(b≠0)
解:bx2=1
x2=
—
∴x=±
b
1
—
b
b
需要讨论
(2)解方程:
x+1
2
——
-
—
1
x
=2
甲同学:方程左右两边同乘以
x(x+1)得
2
x-x-1=
2
x=
3
检验:当x=
3时,x(x+1)
≠0
∴原方程的根为x=
3
常数也要乘以公分母
注意变号
乙同学:方程左右两边同乘以
x(x+1)得
2x-x+1=2x(x+1)
2x2+x-1=0
解得x1=
—
,x2=-1
1
2
经检验:x=-1是增根,舍去
∴原方程的根为
x=
—
2
1
(3)解方程:
x2-3
x
x2-3
3x
+
2
13
=
解:设
=
y,则原方程可化为
2y2-13y+6=0
(2y-1)(y
-6)=0
x
x2-3
∴y1=
—
2
1
,y2=
6
经检验:原方程的根为
y1=
—
2
1
,y2=
6
要回代求x
(4)解方程:
x+1
x2-1
1
3x
3x-3
1
-
=
1
x-1
1
3x
3(x-1)
1
-
=
解:原方程可化为
方程两边同乘以3x(x-1)得
3x-(x-1)=x
解得x=
﹣1
检验:当x=﹣1时,3x(x﹣1)
≠0
∴原方程的根为x=﹣1
代入原方程的最简公分母进行检验
(5)解方程:
x-2
x-3
2
·
=
解:原方程化为
方程左右两边同时平方得
x2-5x
+
6
=
2
x2-5x+4=0
∴x1=1,x2=4
(x-1)(x-4)=0
∴原方程的根为x1=1,x2=4
(x-2)(x-3)
2
=
检验:当
时,原方程左边=右边
x1=1,x2=4
要代入原无理方程进行检验
(6)解方程组:
5x2-y2=11
2x-y=1
①
②
解:由②得y=2x-1③
将③代入①得5x2-(2x-1)2=11
即x2+4x-12=0
解得x1=2,x2=﹣6
把x=2代入①得y=±3
把x=﹣6代入①得y=±13
∴原方程组的解为
x1=2
y1=3
x2=2
y2=﹣3
x1=﹣6
y1=13
x1=﹣6
y1=﹣13
回代二元一次方程求另一个未知数
思想与方法
分式方程
整式方程
检验
原方程的根
去分母
换元
求解
舍去增根
无理方程
有理方程
检验
原方程的根
去根号
求解
舍去增根
由两个二元二次方程组成的方程组
含一次方程的
二元二次方程组
回代求出另一
个未知数的值
原方程组的解
因式分解
代入消元求出一个未知数的值
回家作业:
1、代数方程(卷)
2、补充题(十一)(邮箱)
代数方程复习(二)
分式方程、无理方程、二元二次方程组
分式方程:
分母中含有未知数的有理方程。
无理方程:
根号内含有未知数的方程。
相关概念
二元二次
方程组:
方程组中含有两个未知数,并且含有未知数的项的最高次数为两次,这样的整式方程组叫做二元二次方程组.
1.下列方程中,不是分式方程的是(
)
A
B
C
D
看分母中有没有未知数。
D
练习
2.方程
的解是(
)
A
B
C
D
D
除了使方程左右两边相等外,在分式方程中,首先必须使分式有意义.
3、下列方程有实数根的是(
)
A
4、若关于x的方程
无实数根,则m的取值范围是(
)
(A)大于零
(B)小于零
(C)不大于零
(D)不小于零
B
5、下列方程组中,属于二元二次方程组的是(
)
C
A
B
C
D
2.去分母解分式方程的一般步骤
1、去分母,化成整式方程.
2、解整式方程.
3、代入最简公分母,进行检验。
4、写出原方程的根.
1.解分式方程的思路是:
分式方程
整式方程
去分母
换元后去分母
换元法呢?
例题:
1、解方程:
例题:
解:设x2+x=y,则原方程可化为
y2+y-2=0
去分母并整理得
y1=-2,
y2=1
解得
当y1=-2时,
x2+x=-2,
△<0,无实数根
当y2=1时,
x2+x=1,解得
经检验
是原方程的根.
∴原方程的根是
练习:
_________
3
2
5
)
2
(
_________
1
1
5
)
1
(
的解是
分式方程
的解为
分式方程
x
x
x
=
-
=
+
x=4
x=-3
原方程可化为整式方程:_____________
x+2
x-2
———
-
16
x2-4
———
=
1
x+2
———
(3)
x2+3x-10=0
3x
x2-1
———
+
x2-1
x
———
=
7
2
——
(4)
设_______=y,则原方程可化为
关于y的整式方程为__________
x2-1
———
x
6y2-7y+2=0
练习:
(5)用换元法解方程:
(5)用换元法解方程:
∴y2+y-6=0,即(y+3)(y-2)=0,
y1=-3,y2=2
当y=-3时,x2-x=-3,△<0,无实数根
当y=2时,原方程为x2-x-2=0,x1=2,x2=-1.
经检验x1=2,x2=-1是原方程的根.
∴原方程的根是
x1=2,x2=-1
2.解无理方程的一般步骤
1、通过两边同平方去掉根号,转化为有理方程。
2、解有理方程.
3、代入原方程进行检验。
4、写出原方程的根.
1.解无理方程的思路是:
无理方程
有理方程
平方
例题:
(2)
解方程
x=5
x=0
x1=-5,
x2=1
无实数根
X=20
1.解二元二次方程组的方法是:
(1)代入法:将一个未知数用另一个未知数表示,代入第二个方程,解一元二次方程,然后将求得的未知数的值代回两元一次方程中,求另一个未知数的值,最后写出方程组的解。
(2)因式分解法:将其中一个二元二次方程因式分解成两个一次方程,分别与另一个方程组成方程组,再解方程组。
(1)
x-3y=0
x2+y=20
(2)
x2-3xy+2y2=0
x2+y2=5
本题宜采用_________法
代入消元
本题宜采用__________法
因式分解
解方程组:
消元后的方程为______________
9y2+y-20=0
原方程组可化为以下两个方程组:
x-y=0
x2+y2
=5
x-2y=0
x2+y2
=5
练习:
(3)
(4)
错在哪里?
(1)解关于x的方程:
bx2+1=2(b≠0)
解:bx2=1
x2=
—
∴x=±
b
1
—
b
b
需要讨论
(2)解方程:
x+1
2
——
-
—
1
x
=2
甲同学:方程左右两边同乘以
x(x+1)得
2
x-x-1=
2
x=
3
检验:当x=
3时,x(x+1)
≠0
∴原方程的根为x=
3
常数也要乘以公分母
注意变号
乙同学:方程左右两边同乘以
x(x+1)得
2x-x+1=2x(x+1)
2x2+x-1=0
解得x1=
—
,x2=-1
1
2
经检验:x=-1是增根,舍去
∴原方程的根为
x=
—
2
1
(3)解方程:
x2-3
x
x2-3
3x
+
2
13
=
解:设
=
y,则原方程可化为
2y2-13y+6=0
(2y-1)(y
-6)=0
x
x2-3
∴y1=
—
2
1
,y2=
6
经检验:原方程的根为
y1=
—
2
1
,y2=
6
要回代求x
(4)解方程:
x+1
x2-1
1
3x
3x-3
1
-
=
1
x-1
1
3x
3(x-1)
1
-
=
解:原方程可化为
方程两边同乘以3x(x-1)得
3x-(x-1)=x
解得x=
﹣1
检验:当x=﹣1时,3x(x﹣1)
≠0
∴原方程的根为x=﹣1
代入原方程的最简公分母进行检验
(5)解方程:
x-2
x-3
2
·
=
解:原方程化为
方程左右两边同时平方得
x2-5x
+
6
=
2
x2-5x+4=0
∴x1=1,x2=4
(x-1)(x-4)=0
∴原方程的根为x1=1,x2=4
(x-2)(x-3)
2
=
检验:当
时,原方程左边=右边
x1=1,x2=4
要代入原无理方程进行检验
(6)解方程组:
5x2-y2=11
2x-y=1
①
②
解:由②得y=2x-1③
将③代入①得5x2-(2x-1)2=11
即x2+4x-12=0
解得x1=2,x2=﹣6
把x=2代入①得y=±3
把x=﹣6代入①得y=±13
∴原方程组的解为
x1=2
y1=3
x2=2
y2=﹣3
x1=﹣6
y1=13
x1=﹣6
y1=﹣13
回代二元一次方程求另一个未知数
思想与方法
分式方程
整式方程
检验
原方程的根
去分母
换元
求解
舍去增根
无理方程
有理方程
检验
原方程的根
去根号
求解
舍去增根
由两个二元二次方程组成的方程组
含一次方程的
二元二次方程组
回代求出另一
个未知数的值
原方程组的解
因式分解
代入消元求出一个未知数的值
回家作业:
1、代数方程(卷)
2、补充题(十一)(邮箱)
