人教版数学七年级上册3.4.1实际问题与一元一次方程——配套问题课件(共22张ppt)
文档属性
| 名称 | 人教版数学七年级上册3.4.1实际问题与一元一次方程——配套问题课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 571.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 21:28:29 | ||
图片预览







文档简介
(共22张PPT)
桌面
桌腿
眼镜
镜片
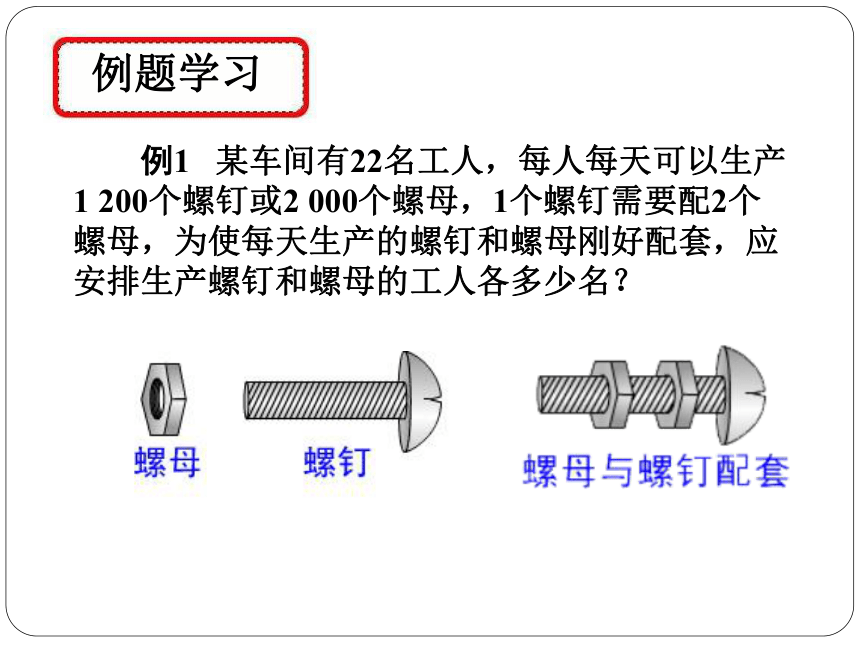
螺母
螺钉
人教版数学七年级上册
3.4
实际问题与一元一次方程(1)
配套问题
学习目标:
1、会通过列方程解决“配套
问题”。
2、掌握列方程解决实际问题的一般步骤。
3、通过列方程解决实际问题的过程,体会建模思想。
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例题学习
(1)本题中有哪些已知条件?要求什么?
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
(2)题目中有哪些等量关系?
例题学习
(3)直接设生产螺钉的人数为x人,将上述信息在下列表格中表示出来:
(22-x)
1200x
2000(22-x)
x
产品类型
单人产量
生产人数
总产量
螺钉
螺母
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
1
200
2
000
例题学习
这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据.
解:设应安排
x
名工人生产螺钉,________名工人生产螺母.
由题意列出方程:
2
000
(
22
-x)=2×1
200
x.
(22
-
x)
(22-x)
1200x
2000(22-x)
x
产品类型
生产人数
单人产量
总产量
螺钉
1
200
螺母
2
000
如果设x名工人生产螺母,怎样列方程?
(22-x)
2000x
1200
(22-x)
x
产品类型
生产人数
单人产量
总产量
螺钉
1
200
螺母
2
000
解:设应安排
x
名工人生产螺母,________名工人生产螺钉.
由题意列出方程:
(22
-
x)
例题学习
螺母数量=2×螺钉数量
(4)还可以怎样理解刚好配套,你还能得到什么等量关系?
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
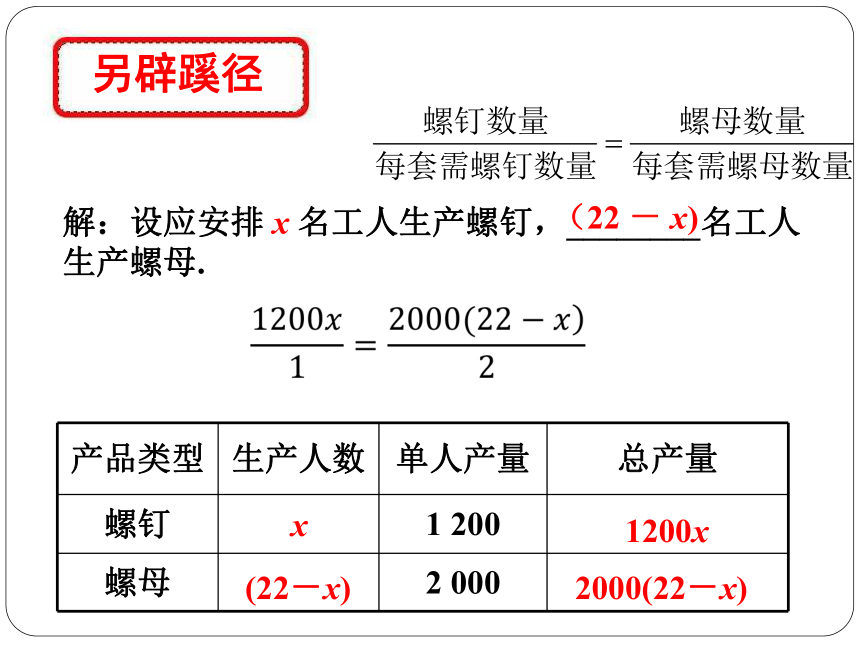
螺钉的套数
螺母的套数
=
另辟蹊径
解:设应安排
x
名工人生产螺钉,________名工人生产螺母.
(22
-
x)
(22-x)
1200x
2000(22-x)
x
产品类型
生产人数
单人产量
总产量
螺钉
1
200
螺母
2
000
另辟蹊径
(5)可以间接设生产螺钉总数为未知数吗?
又该使用哪个等量关系列方程呢?
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
再探例题
解:设生产螺钉个数为y个,螺母个数为2y个.
列方程:
解方程,得
5y
+6y
=
132000
11y
=
13200
,
y
=
12000
22
-
10
=
12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
再探例题
你能说出
列一元一次方程解应用题的
一般步骤吗?
某车间有工人55人,每人每天可以加工大齿轮8个或小齿轮10个,并且每人每天只能加工一种齿轮。
(2)若3个大齿轮和4个小齿轮配为一套时,还能通过安排劳力使产品刚好配套吗?
(1)若2个大齿轮和3个小齿轮配为一套时,应如何安排劳力使生产的产品刚好成套?
学以致用
用一元一次方程解决实际问题的基本过程如下:
实际问题
解方程
一元一次方程的解(x=a)
检验
实际问题
的答案
设未知数、
列方程
一元一次方程
模型思想
归纳总结
审
谈谈你们的收获。。。
课本P106习题3.4第2、3题.
基本要求:用一种方法完成即可.
(选做)提高要求:用两种不同的方法完成.
课后作业
谢谢指导!
练一练:1.某车间有28名工人生产螺栓和螺母,每人每小时平均能生产螺栓12个或螺母18个,应如何分配生产螺栓和螺母的工人,才能使螺栓和螺母正好配套(一个螺栓配两个螺母)?
2.包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,将两张圆形铁片和一张长方形铁片可配套成一个密封圆桶,问如何安排工人生产圆形或长方形铁片能合理地将铁片配套?
2.某糕点厂中秋节前要制作一批盒装月饼,每盒中装3块大月饼和5块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
解:设制作大、小月饼分别用面粉xkg和(4500-x)kg,可列方程
解方程,得
x=2700.
4500-x=1800.
答:制作大、小月饼分别用面粉2700kg和1800kg.
相等关系:5×大月饼数=3×小月饼数
解:设能生产月饼y盒,则大月饼有3y个,小月饼有5y个,根据题意,可列方程
解方程,得
y=18000.
答:制作大、小月饼分别用面粉2700kg和1800kg.
2.某糕点厂中秋节前要制作一批盒装月饼,每盒中装3块大月饼和5块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
相等关系:大月饼所需面粉+小月饼所需面粉=4500
3.有以下问题:某服装厂要生产校服一批,已知每3m2的布料可以制作上衣两件或裤子3条.计划用300m2的布料生产校服,应分别用多少布料制作上衣和裤子,可生产校服多少套?对此问题,小方和小程有不同的解法,他们做得对吗?
小方同学的解法是:设用xm2制作上衣,(300-x)m2制作裤子,可列方程
解得x=180,300-x=120.
答:应用180m2制作上衣,120m2制作裤子,可生产校服120套.
小程同学的解法是:设可生产校服y套,可列方程
解得y=120.
,
300
-
180=120.
答:应用180m2制作上衣,120m2制作裤子,可生产校服120套.
3.有以下问题:某服装厂要生产校服一批,已知每3m2的布料可以制作上衣两件或裤子3条.计划用300m2的布料生产校服,应分别用多少布料制作上衣和裤子,可生产校服多少套?对此问题,小方和小程有不同的解法,他们做得对吗?
桌面
桌腿
眼镜
镜片
螺母
螺钉
人教版数学七年级上册
3.4
实际问题与一元一次方程(1)
配套问题
学习目标:
1、会通过列方程解决“配套
问题”。
2、掌握列方程解决实际问题的一般步骤。
3、通过列方程解决实际问题的过程,体会建模思想。
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例题学习
(1)本题中有哪些已知条件?要求什么?
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
(2)题目中有哪些等量关系?
例题学习
(3)直接设生产螺钉的人数为x人,将上述信息在下列表格中表示出来:
(22-x)
1200x
2000(22-x)
x
产品类型
单人产量
生产人数
总产量
螺钉
螺母
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
1
200
2
000
例题学习
这类问题中配套的物品之间具有一定的数量关系,这可以作为列方程的依据.
解:设应安排
x
名工人生产螺钉,________名工人生产螺母.
由题意列出方程:
2
000
(
22
-x)=2×1
200
x.
(22
-
x)
(22-x)
1200x
2000(22-x)
x
产品类型
生产人数
单人产量
总产量
螺钉
1
200
螺母
2
000
如果设x名工人生产螺母,怎样列方程?
(22-x)
2000x
1200
(22-x)
x
产品类型
生产人数
单人产量
总产量
螺钉
1
200
螺母
2
000
解:设应安排
x
名工人生产螺母,________名工人生产螺钉.
由题意列出方程:
(22
-
x)
例题学习
螺母数量=2×螺钉数量
(4)还可以怎样理解刚好配套,你还能得到什么等量关系?
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
螺钉的套数
螺母的套数
=
另辟蹊径
解:设应安排
x
名工人生产螺钉,________名工人生产螺母.
(22
-
x)
(22-x)
1200x
2000(22-x)
x
产品类型
生产人数
单人产量
总产量
螺钉
1
200
螺母
2
000
另辟蹊径
(5)可以间接设生产螺钉总数为未知数吗?
又该使用哪个等量关系列方程呢?
例1
某车间有22名工人,每人每天可以生产1
200个螺钉或2
000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
再探例题
解:设生产螺钉个数为y个,螺母个数为2y个.
列方程:
解方程,得
5y
+6y
=
132000
11y
=
13200
,
y
=
12000
22
-
10
=
12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
再探例题
你能说出
列一元一次方程解应用题的
一般步骤吗?
某车间有工人55人,每人每天可以加工大齿轮8个或小齿轮10个,并且每人每天只能加工一种齿轮。
(2)若3个大齿轮和4个小齿轮配为一套时,还能通过安排劳力使产品刚好配套吗?
(1)若2个大齿轮和3个小齿轮配为一套时,应如何安排劳力使生产的产品刚好成套?
学以致用
用一元一次方程解决实际问题的基本过程如下:
实际问题
解方程
一元一次方程的解(x=a)
检验
实际问题
的答案
设未知数、
列方程
一元一次方程
模型思想
归纳总结
审
谈谈你们的收获。。。
课本P106习题3.4第2、3题.
基本要求:用一种方法完成即可.
(选做)提高要求:用两种不同的方法完成.
课后作业
谢谢指导!
练一练:1.某车间有28名工人生产螺栓和螺母,每人每小时平均能生产螺栓12个或螺母18个,应如何分配生产螺栓和螺母的工人,才能使螺栓和螺母正好配套(一个螺栓配两个螺母)?
2.包装厂有工人42人,每个工人平均每小时可以生产圆形铁片120片,或长方形铁片80片,将两张圆形铁片和一张长方形铁片可配套成一个密封圆桶,问如何安排工人生产圆形或长方形铁片能合理地将铁片配套?
2.某糕点厂中秋节前要制作一批盒装月饼,每盒中装3块大月饼和5块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
解:设制作大、小月饼分别用面粉xkg和(4500-x)kg,可列方程
解方程,得
x=2700.
4500-x=1800.
答:制作大、小月饼分别用面粉2700kg和1800kg.
相等关系:5×大月饼数=3×小月饼数
解:设能生产月饼y盒,则大月饼有3y个,小月饼有5y个,根据题意,可列方程
解方程,得
y=18000.
答:制作大、小月饼分别用面粉2700kg和1800kg.
2.某糕点厂中秋节前要制作一批盒装月饼,每盒中装3块大月饼和5块小月饼.制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉.现共有面粉4500kg,制作两种月饼应各用多少面粉,才能生产最多的盒装月饼?
相等关系:大月饼所需面粉+小月饼所需面粉=4500
3.有以下问题:某服装厂要生产校服一批,已知每3m2的布料可以制作上衣两件或裤子3条.计划用300m2的布料生产校服,应分别用多少布料制作上衣和裤子,可生产校服多少套?对此问题,小方和小程有不同的解法,他们做得对吗?
小方同学的解法是:设用xm2制作上衣,(300-x)m2制作裤子,可列方程
解得x=180,300-x=120.
答:应用180m2制作上衣,120m2制作裤子,可生产校服120套.
小程同学的解法是:设可生产校服y套,可列方程
解得y=120.
,
300
-
180=120.
答:应用180m2制作上衣,120m2制作裤子,可生产校服120套.
3.有以下问题:某服装厂要生产校服一批,已知每3m2的布料可以制作上衣两件或裤子3条.计划用300m2的布料生产校服,应分别用多少布料制作上衣和裤子,可生产校服多少套?对此问题,小方和小程有不同的解法,他们做得对吗?
