沪教版(上海)初中数学七年级第一学期 10.1 分式的意义 教案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 10.1 分式的意义 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
10.1
分式的意义
一.教材分析:
本节课的主要内容是分式的概念以及掌握分式有意义、无意义、分式值为0的条件.它是在学生掌握了整式的概念、变形、四则运算及因式分解的基础上,并以六年级第一学期的分数知识为基础,对比引出分式的概念,把学生对“式”的认识由整式扩充到有理式.学好本节知识是为进一步学习分式知识打下扎实的基础,是以后学习函数、方程等问题的关键。
二.学情分析:
七年级学生通过六年级分数的学习,已形成了分数的相关知识,知道分数的分子、分母都是具体的数,因此学生可能会用学习分数的思维定势去认知、理解分式.但是在分式中,它的分母不是具体的数,而是抽象的含有字母的整式,会随着字母取值的变化而变化.为了学生能切实掌握所学知识,在教学中特别设计了几组练习;对于教材中的例题和练习题,将作适当的延伸拓展和变式处理.
学生在本节课中可能遇到的困难:
1.容易受分数“形似”的影响而忽略分式的本质:分母中含有字母,分子分母均为整式;
2.分式有意义的条件是分母≠0,却在过分强调分式与整式的区别后错误的认为是分母中的字母≠0;
3.分式值为0时,只考虑分子为0,而忽视前提是分母≠0。
三.教学目标:
1.通过现实情境,在已有数学经验的基础上,了解数学的价值,进一步理解用字母表示数的意义,感悟数学来源于现实生活,培养“用数学”的信心。
2.通过观察探究,体会整式与分式的区别,经历分式的形成过程,理解分式的概念,以及分式与整式概念的区别与联系;通过与分数类比学习分式的过程,养成缜密的思维习惯,体会类比思想。
3.通过对具体分式的探究与讨论,发现分式无意义、有意义、分式值为零时应满足的条件并熟练应用,学会从具体到抽象、从特殊到一般的发现问题与解决问题的方法。
四.教学重点和难点:
1.教学重点:正确理解分式的概念、分式的意义。
2.教学难点:理解和掌握分式值为0的条件。
五.教学过程:
学习内容
教学环节
教师活动
学生活动
设计意图
一.分式的概念
(一).创设情景,校对预习作业
情景:欣赏上海迪士尼的相关图片.问题1:你能用代数式表示以下问题中要求的量吗?1.预测上海迪士尼乐园的游客每年可达5千万人,请问平均每个月约有几千万人参观?
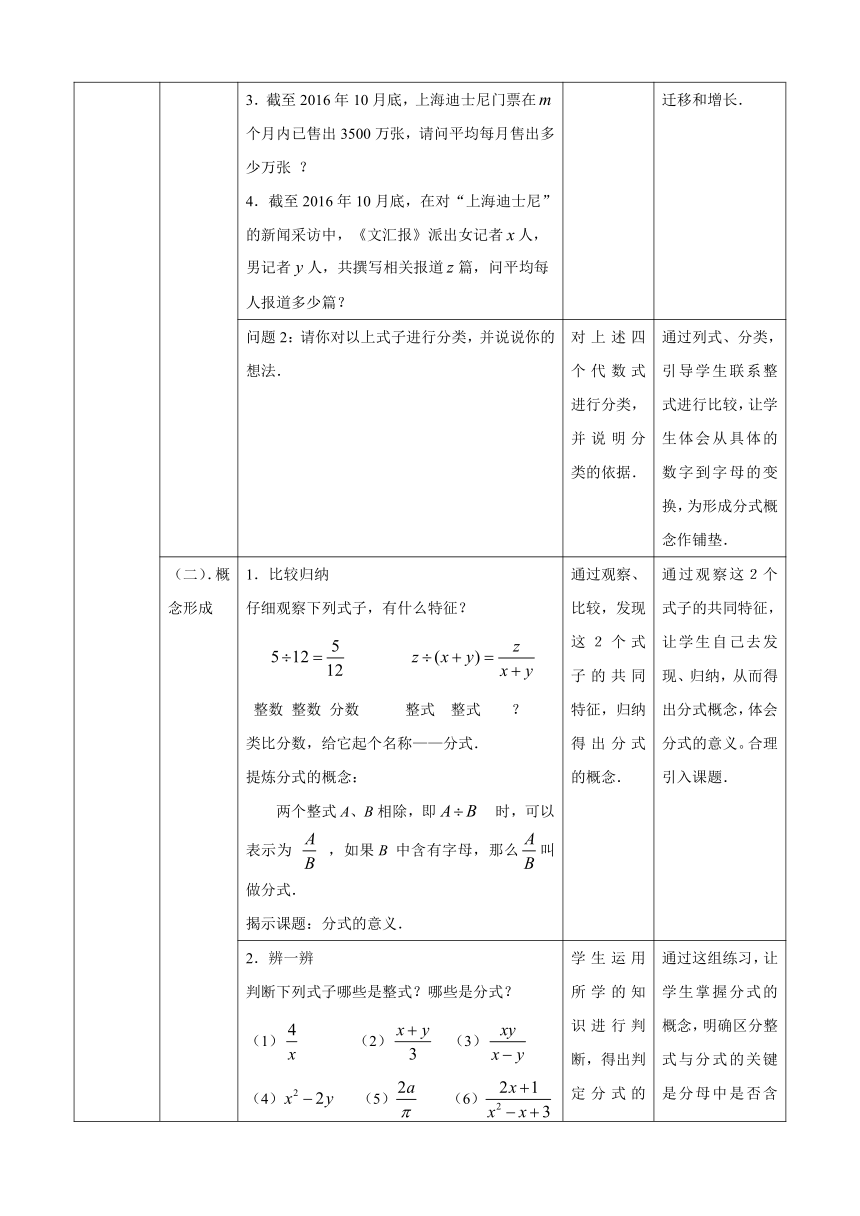
2.上海迪士尼开园以后,吸引了不少的外国游客。全世界共有224个国家和地区,到目前为止,共有个国家和地区的游客前来参观和游玩。请问已经有游客来迪士尼的国家占全球国家总数的几分之几?3.截至2016年10月底,上海迪士尼门票在个月内已售出3500万张,请问平均每月售出多少万张
?4.截至2016年10月底,在对“上海迪士尼”的新闻采访中,《文汇报》派出女记者人,男记者人,共撰写相关报道篇,问平均每人报道多少篇?
学生交流列式.
以学生关注、喜爱的迪士尼为情景,让学生充分体会数学来源于现实生活,激发学生的学习热情,形成良好的学习氛围。通过问题,引导学生联系已有的知识,实现知识的类比、迁移和增长.
问题2:请你对以上式子进行分类,并说说你的想法.
对上述四个代数式进行分类,并说明分类的依据.
通过列式、分类,引导学生联系整式进行比较,让学生体会从具体的数字到字母的变换,为形成分式概念作铺垫.
(二).概念形成
1.比较归纳仔细观察下列式子,有什么特征?
整数
整数
分数
整式
整式
?类比分数,给它起个名称——分式.
提炼分式的概念:两个整式A、B相除,即
时,可以表示为
,如果B
中含有字母,那么叫做分式.
揭示课题:分式的意义.
通过观察、比较,发现这2个式子的共同特征,归纳得出分式的概念.
通过观察这2个式子的共同特征,让学生自己去发现、归纳,从而得出分式概念,体会分式的意义。合理引入课题.
2.辨一辨判断下列式子哪些是整式?哪些是分式?(1)
(2)
(3)(4)
(5)
(6)说说区分整式与分式的关键是什么?
学生运用所学的知识进行判断,得出判定分式的方法.
通过这组练习,让学生掌握分式的概念,明确区分整式与分式的关键是分母中是否含有字母.
3.编一编在下列整式中,任选两个作为分子分母,构造三个分式:挑选一个简单的分式,
结合生活实际,试着赋予分式实际意义,并交流.
学生写出多个分式,通过交流,从中选择一个简单的分式,试着赋予分式实际意义.
通过开放性的编写分式,让学生体会掌握知识的乐趣、创造知识的快感,并把知识于应用于生活。在活动过程中强化分式概念,并及时纠正学生可能因分数负迁移所造成的认知障碍.
二.分式有意义的条件与分式的值为0 的条件
校对预习作业
(1)已知代数式
,求当时代数式的值.(2)任选一个你喜欢的数,求此时这个代数式的值.
交流计算结果.
在规定要求和自选数字中产生碰撞,为分式有意义的条件做铺垫.
交流探究
问题1:可以取任意的有理数吗?为什么不取1呢?(引导学生由分数与除法的关系,分母不能为零。由于分式也是由除法转变而来,分式的分母也有同样的要求)小结并板书:分式有意义,分母不能为零;分母为零,分式无意义。(在探讨过程中,教师应引导学生注意不是字母的值是否为0,而是表示分母的整式的值是否为0,这也是学生容易混淆的地方。)
经过互动交流,达成共识,得出分式有意义,无意义的条件.
通过操作探究,让学生经历了分式有意义的探究过程,避免以往概念教学的机械记忆,同时发展了学生的探究意识,培养学生思维的广阔性.
讨论2:有没有同学取-1呢?若取-1,结果怎样?深入思考:是不是分子为零时,分式的值一定为零?举例说明:分式
,当=
时,分式的值为零。小结并板书:分式值为零的条件:分式的分子为零,且分母不为零。(引导学生认识分式为零的前提是分式有意义)
思考并口答,学习教师的示范板书.
启发并引导学生自己去发现,归纳,总结出分式值为零的条件,从而使学生获得成功的体验,培养学生归纳、概括的能力.
例题学习:
对于分式
(1)当取什么值时,分式有意义?变式训练:当取何值时,分式无意义?(2)当取什么值时,分式的值为零?试练:对于分式(1)要使分式有意义,和需满足什么条件?(2)要使分式值为零,和需满足什么条件?
试一试,通过解题过程的书写,训练规范书写的格式,培养思维的条理性.
例题的选择由浅入深,循序渐进,体现渐进原则,突破难点的目的.
巩固与提升
(1)当
时,分式有意义.(2)当时,对于分式
,正确的答案是(
).A.值为零
B.无意义(3)当
时,分式
值为零.(4)设计一个分式,不管字母取何值,使这个分式都有意义.
学生进行自我检测与自我评价,同时进行提升,体会某些分式的恒有意义.
及时对所学知识进行进一步的深化应用,以使学生对知识点的掌握情况及时检测,也使教师及时了解并进行有针对性指导.
课堂小结
1.通过本节课的学习,你有什么收获?(知识、能力、数学思想方法等)2.你还有什么疑问吗?
布置作业
分式的意义
一.教材分析:
本节课的主要内容是分式的概念以及掌握分式有意义、无意义、分式值为0的条件.它是在学生掌握了整式的概念、变形、四则运算及因式分解的基础上,并以六年级第一学期的分数知识为基础,对比引出分式的概念,把学生对“式”的认识由整式扩充到有理式.学好本节知识是为进一步学习分式知识打下扎实的基础,是以后学习函数、方程等问题的关键。
二.学情分析:
七年级学生通过六年级分数的学习,已形成了分数的相关知识,知道分数的分子、分母都是具体的数,因此学生可能会用学习分数的思维定势去认知、理解分式.但是在分式中,它的分母不是具体的数,而是抽象的含有字母的整式,会随着字母取值的变化而变化.为了学生能切实掌握所学知识,在教学中特别设计了几组练习;对于教材中的例题和练习题,将作适当的延伸拓展和变式处理.
学生在本节课中可能遇到的困难:
1.容易受分数“形似”的影响而忽略分式的本质:分母中含有字母,分子分母均为整式;
2.分式有意义的条件是分母≠0,却在过分强调分式与整式的区别后错误的认为是分母中的字母≠0;
3.分式值为0时,只考虑分子为0,而忽视前提是分母≠0。
三.教学目标:
1.通过现实情境,在已有数学经验的基础上,了解数学的价值,进一步理解用字母表示数的意义,感悟数学来源于现实生活,培养“用数学”的信心。
2.通过观察探究,体会整式与分式的区别,经历分式的形成过程,理解分式的概念,以及分式与整式概念的区别与联系;通过与分数类比学习分式的过程,养成缜密的思维习惯,体会类比思想。
3.通过对具体分式的探究与讨论,发现分式无意义、有意义、分式值为零时应满足的条件并熟练应用,学会从具体到抽象、从特殊到一般的发现问题与解决问题的方法。
四.教学重点和难点:
1.教学重点:正确理解分式的概念、分式的意义。
2.教学难点:理解和掌握分式值为0的条件。
五.教学过程:
学习内容
教学环节
教师活动
学生活动
设计意图
一.分式的概念
(一).创设情景,校对预习作业
情景:欣赏上海迪士尼的相关图片.问题1:你能用代数式表示以下问题中要求的量吗?1.预测上海迪士尼乐园的游客每年可达5千万人,请问平均每个月约有几千万人参观?
2.上海迪士尼开园以后,吸引了不少的外国游客。全世界共有224个国家和地区,到目前为止,共有个国家和地区的游客前来参观和游玩。请问已经有游客来迪士尼的国家占全球国家总数的几分之几?3.截至2016年10月底,上海迪士尼门票在个月内已售出3500万张,请问平均每月售出多少万张
?4.截至2016年10月底,在对“上海迪士尼”的新闻采访中,《文汇报》派出女记者人,男记者人,共撰写相关报道篇,问平均每人报道多少篇?
学生交流列式.
以学生关注、喜爱的迪士尼为情景,让学生充分体会数学来源于现实生活,激发学生的学习热情,形成良好的学习氛围。通过问题,引导学生联系已有的知识,实现知识的类比、迁移和增长.
问题2:请你对以上式子进行分类,并说说你的想法.
对上述四个代数式进行分类,并说明分类的依据.
通过列式、分类,引导学生联系整式进行比较,让学生体会从具体的数字到字母的变换,为形成分式概念作铺垫.
(二).概念形成
1.比较归纳仔细观察下列式子,有什么特征?
整数
整数
分数
整式
整式
?类比分数,给它起个名称——分式.
提炼分式的概念:两个整式A、B相除,即
时,可以表示为
,如果B
中含有字母,那么叫做分式.
揭示课题:分式的意义.
通过观察、比较,发现这2个式子的共同特征,归纳得出分式的概念.
通过观察这2个式子的共同特征,让学生自己去发现、归纳,从而得出分式概念,体会分式的意义。合理引入课题.
2.辨一辨判断下列式子哪些是整式?哪些是分式?(1)
(2)
(3)(4)
(5)
(6)说说区分整式与分式的关键是什么?
学生运用所学的知识进行判断,得出判定分式的方法.
通过这组练习,让学生掌握分式的概念,明确区分整式与分式的关键是分母中是否含有字母.
3.编一编在下列整式中,任选两个作为分子分母,构造三个分式:挑选一个简单的分式,
结合生活实际,试着赋予分式实际意义,并交流.
学生写出多个分式,通过交流,从中选择一个简单的分式,试着赋予分式实际意义.
通过开放性的编写分式,让学生体会掌握知识的乐趣、创造知识的快感,并把知识于应用于生活。在活动过程中强化分式概念,并及时纠正学生可能因分数负迁移所造成的认知障碍.
二.分式有意义的条件与分式的值为0 的条件
校对预习作业
(1)已知代数式
,求当时代数式的值.(2)任选一个你喜欢的数,求此时这个代数式的值.
交流计算结果.
在规定要求和自选数字中产生碰撞,为分式有意义的条件做铺垫.
交流探究
问题1:可以取任意的有理数吗?为什么不取1呢?(引导学生由分数与除法的关系,分母不能为零。由于分式也是由除法转变而来,分式的分母也有同样的要求)小结并板书:分式有意义,分母不能为零;分母为零,分式无意义。(在探讨过程中,教师应引导学生注意不是字母的值是否为0,而是表示分母的整式的值是否为0,这也是学生容易混淆的地方。)
经过互动交流,达成共识,得出分式有意义,无意义的条件.
通过操作探究,让学生经历了分式有意义的探究过程,避免以往概念教学的机械记忆,同时发展了学生的探究意识,培养学生思维的广阔性.
讨论2:有没有同学取-1呢?若取-1,结果怎样?深入思考:是不是分子为零时,分式的值一定为零?举例说明:分式
,当=
时,分式的值为零。小结并板书:分式值为零的条件:分式的分子为零,且分母不为零。(引导学生认识分式为零的前提是分式有意义)
思考并口答,学习教师的示范板书.
启发并引导学生自己去发现,归纳,总结出分式值为零的条件,从而使学生获得成功的体验,培养学生归纳、概括的能力.
例题学习:
对于分式
(1)当取什么值时,分式有意义?变式训练:当取何值时,分式无意义?(2)当取什么值时,分式的值为零?试练:对于分式(1)要使分式有意义,和需满足什么条件?(2)要使分式值为零,和需满足什么条件?
试一试,通过解题过程的书写,训练规范书写的格式,培养思维的条理性.
例题的选择由浅入深,循序渐进,体现渐进原则,突破难点的目的.
巩固与提升
(1)当
时,分式有意义.(2)当时,对于分式
,正确的答案是(
).A.值为零
B.无意义(3)当
时,分式
值为零.(4)设计一个分式,不管字母取何值,使这个分式都有意义.
学生进行自我检测与自我评价,同时进行提升,体会某些分式的恒有意义.
及时对所学知识进行进一步的深化应用,以使学生对知识点的掌握情况及时检测,也使教师及时了解并进行有针对性指导.
课堂小结
1.通过本节课的学习,你有什么收获?(知识、能力、数学思想方法等)2.你还有什么疑问吗?
布置作业
