沪教版(上海)初中数学七年级第一学期 11.1 平移 教案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 11.1 平移 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 734.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 06:32:34 | ||
图片预览



文档简介
教学设计
教学设计
一、教学背景与设计
学科
数学
所用教材
沪教版
任课教师
年级班级
课
题
11.1平移
本课教材分析
图形的运动是空间与图形领域中一块重要的内容。通过图形的运动使图形动起来,有助于在运动的过程中发现图形的变与不变性。因此,图形的运动是研究几何问题,发现结论的有效工具。而平移是沪教版七年级上册第十一章《图形的运动》第一节,引入平移运动,可以渗透图形的运动思想,使学生尽早尝试利用平移知识分析和解决问题。而本节主要讨论的是平移运动的基本性质,要求学生对平移有一个初步的认识。
课标要求及解读
了解平移的特征,能发现、归纳图形平移的特征。让学生经历观察、操作、探究、归纳等过程,总结平移的基本特征,进一步发展学生的抽象概括能力。让学生经历操作、实验、发现归纳等数学活动,感受数学活动的探索性和创造性。激发学生的探究人情,感受数学的美。
本课教学目标
1.在经历图形平移概念形成的过程中,培养数学语言概括能力,归纳出图形平移后图形的形状、大小保持不变的性质.2.知道对应点、对应角、对应线段的概念,并由概念得到平移的性质.3.会在方格纸上画出经过平移后的平面图形,初步体会图形运动.掌握平移方向的意义,会画出平移方向,量出平移距离.
学情分析
本节课采用的是开放式和探究式的教学方法,让学生通过探究,了解平移的特征,建构平移的概念,并采用多媒体辅助教学,演示平移变换的过程,激发学生的积极形,通过展示图片,体现数学的美的存在。
四步教学实施步骤
自学
(描述“自学”阶段你所设计的活动)通过微视频进行预学习并完成预学习单
交流
(描述“交流”阶段你所设计的活动)交流预学习知识并交流预学习留下的思考
指导
(描述“指导”阶段你所设计的活动)平移的性质以及平移中涉及的概念
反馈
(描述“反馈”阶段你所设计的活动)通过课堂练习反馈所学知识
教学重点
图形平移的性质
教学难点
图形平移的概念形成.
二、实施过程:
教师活动
学生活动
设计意图
一.自学师:在日常生活中我们会看到这样一些现象.请看大屏幕:课件演示直升飞机螺旋桨的运动、汽车在笔直的马路上行驶、蝴蝶翅膀的翻折运动.问:刚才我们看到了物体的有关运动,你能说出它们是什么运动吗?师:通过刚才的实例,如果我们把直升飞机螺旋桨、汽车、蝴蝶翅膀抽象成平面图形,这些实例就给我们以图形的三种基本运动形式的直观感受,在第十一章我们主要来学习平面中图形的运动.师:汽车在笔直马路上行驶实际上是物体的平移,若将地面看作平面,汽车看成是平面图形,那么就可以看作图形在平面中平移,那么图形究竟作怎样的运动才是平移呢?
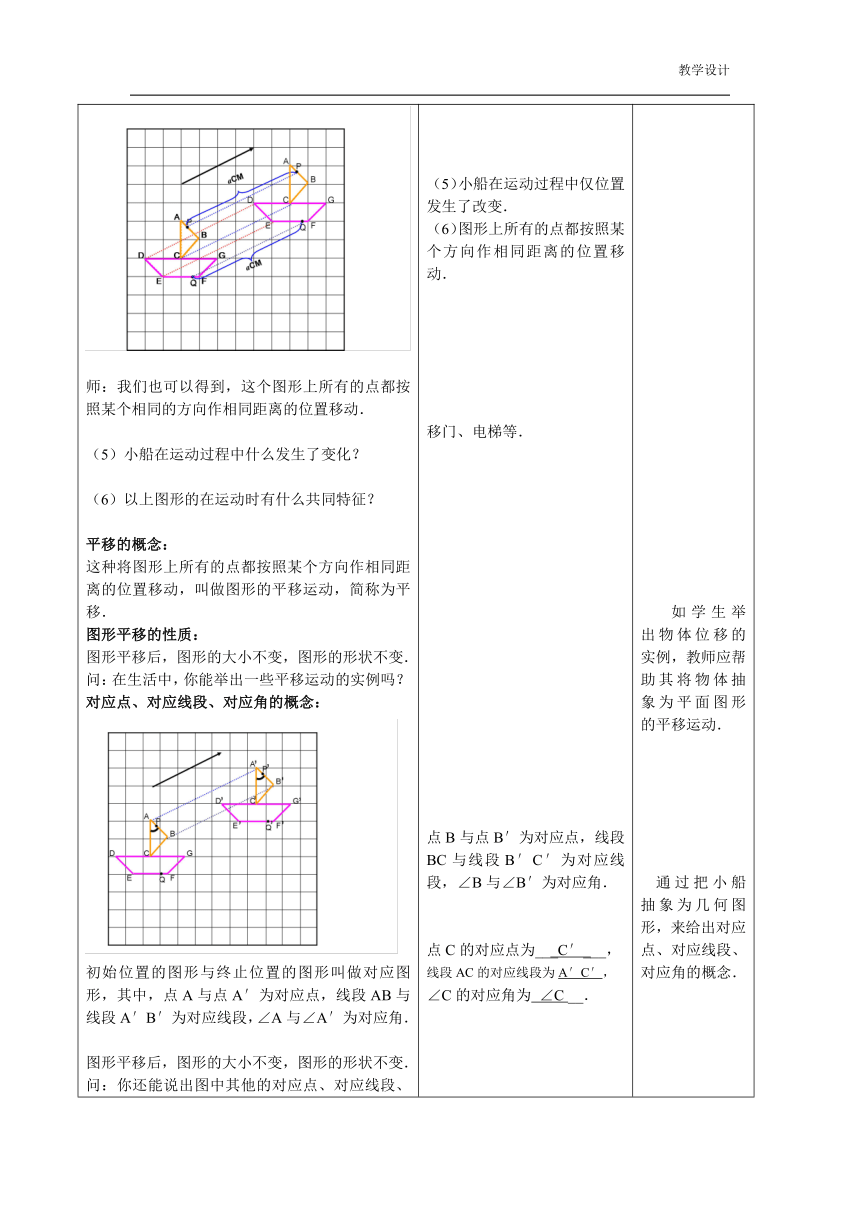
思考:(1)从小船运动的现象中你发现小船运动的方向有什么特征吗?(2)如果在船头停着一只红鸟,船尾停着一只蓝鸟,当小船停靠岸时,两只小鸟发生了激烈的争吵.红鸟说:“我停在船头,经过的路长一点.”蓝鸟说:“不对不对,我停在船尾,经过的路长一点哩.”请同学们评评理,究竟谁经过的距离长一点?(3)如果小鸟停在船的如图所示的特殊的地方,而且小船沿着箭头所指的方向行驶,那么两只小鸟经过的距离又会怎样呢?
(4)将小鸟看作为一点,放在任意地方,如点P、点Q处,小鸟经过的距离又会怎样呢?你发现了什么规律?师:我们也可以得到,这个图形上所有的点都按照某个相同的方向作相同距离的位置移动.(5)小船在运动过程中什么发生了变化?(6)以上图形的在运动时有什么共同特征?
平移的概念:这种将图形上所有的点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移.图形平移的性质:图形平移后,图形的大小不变,图形的形状不变.问:在生活中,你能举出一些平移运动的实例吗?对应点、对应线段、对应角的概念:初始位置的图形与终止位置的图形叫做对应图形,其中,点A与点A′为对应点,线段AB与线段A′B′为对应线段,∠A与∠A′为对应角.图形平移后,图形的大小不变,图形的形状不变.问:你还能说出图中其他的对应点、对应线段、对应角吗?练习:如图,平移△ABC就可以得到△A′B′C′,点C的对应点为_________,线段AC的对应线段为_________,∠C的对应角为_________.二、交流例题1
画出△ABC向右平移4格,向下平移3格后的图形.问1:△ABC平移后所得的图形是什么?
问2:怎样画出平移后的三角形?为什么?解:(i)如图,分别画出点A、B、C向右平移4格,向下平移3格后所对应的点A1、B1、C1;(ii)联结A1B1、B1C1、A1C1,得△A1B1C1.△A1B1C就是所求作的图形.三、指导例题1
画出△ABC向右平移4格,向下平移3格后的图形.大屏幕播放:后面一个三角形是由前面的三角形平移得到的.请同学们拿出度量工具量一量:验证图形平移的性质图形平移的性质:1.图形平移后,对应点之间的距离相等、对应线段的长度、对应角的大小相等.2.图形平移后,图形的大小不变,图形的形状不变.平移的距离:平移后各对应点之间的距离叫做图形平移的距离.问:在练习题中,你能说出△ABC与到△A′B′C′平移的距离吗?为什么?问3:你能画出上图中△ABC平移的方向,并量出平移的距离吗?例2
如图把四边形向左平移4格,再向下平移2格,画出平移后的图形,并画出平移方向,量出平移的距离.问:此题需要分别画出几个点的对应点?【适时小结】1.要画出平移后的多边形的图形,关键在于找到这个多边形的各个顶点平移后的对应点的位置.2.平移方向与平移操作是不同的,平移操作仅限于在方格纸上将图形沿着水平方向或竖直方向做平移运动,平移方向只关注平移图形的初始位置.四、反馈课堂练习:1.平移改变的是图形的(
)A、形状
B、位置 C、大小 D、形状、大小及位置2.∠DEF是∠ABC经过平移得到的,如果∠ABC=45°,那么∠DEF的度数为
.为什么?3.在下面六幅图案中,图案(2)、(3)、(4)、(5)、(6)中的哪个图案可以通过平移图案(1)得到?4、如图,把箭头状图形向右平移4格,向下平移2格,画出平移后的图形.5、图中的四个小三角形都是边长为2cm的等边三角形,平移△ABC能与哪些三角形重合?6、有一块边长为101m的正方形稻田,,稻田里有纵横各两条水渠,渠宽都是0.5m,问稻田的种植面积是多少?五.课堂小结:本节课你有哪些收获与体会?
图形平移的概念.图形平移的性质.
直升飞机螺旋桨的运动:旋转汽车在笔直的马路上行驶:平移.蝴蝶翅膀的翻折:翻折.(1)小船按照从左到右的方向移动.(2)红鸟与蓝鸟经过的距离相等,都是7个单位.(3)两只小鸟经过的距离仍然相等.无论小鸟停在船的任何位置,它们移动的方向和距离都相等.(4)小鸟经过的距离仍然相等.无论小鸟停在船的任何位置,它们移动的距离都相等.(5)小船在运动过程中仅位置发生了改变.(6)图形上所有的点都按照某个方向作相同距离的位置移动.移门、电梯等.点B与点B′为对应点,线段BC与线段B′C′为对应线段,∠B与∠B′为对应角.点C的对应点为___C′___,线段AC的对应线段为A′C′,∠C的对应角为
∠C
__.问1:△ABC平移后所得的图形仍然是三角形.问2:由于图形经过平移运动后,图形上的任何一点平移的距离都相等,所以只需分别画出A、B、C三点平移后的对应点,再联结各点,就可以得到平移后的三角形.△ABC与到△A′B′C′平移的距离为对应点之间的距离相等,所以只需测量出两个三角形中的一个点与它的对应点之间的距离即可.平移的方向为射线A
A1或射线B
B1、CC1的方向.平移的距离为线段A
A1或线段B
B1、CC1的长度.B2.∠DEF=45°,图形平移后,对应角的大小相等.3.(3)5.平移△ABC能与△ECD、△FAE重合.6、解:(101-0.5×2)2=1002=10000m2答:稻田的种植面积是10000
m2.1.平移的概念:这种将图形上所有的点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移.2.图形平移的性质:(1)图形平移后,对应点之间的距离相等、对应线段的长度、对应角的大小相等.(2)图形平移后,图形的大小不变,图形的形状不变.
从现实生活中具体实例抽象出数学问题,感受图形的基本运动.根据生活中物体位移进一步抽象到平面中图形的平移,引导学生根据自己生活中已有的经验,形成图形平移的概念.如学生举出物体位移的实例,教师应帮助其将物体抽象为平面图形的平移运动.通过把小船抽象为几何图形,来给出对应点、对应线段、对应角的概念.让学生认识到,要画出平移后的三角形的图形,关键在于找到这个三角形的三个顶点(特殊点)平移后的对应点的位置.教师引导学生动手测量图形运动前后对应边的长度、对应角的大小及对应点之间的距离等,验证图形平移的性质.补充例2,画一个四边形平移后的图形,让学生进一步理解画平移后的图形关键在于找到这个多边形的各个顶点平移后的对应点的位置.巩固新知,运用新知,突出重点,反馈调控.
梳理本节课知识,教师进一步提炼总结,提升学生的认识水平.
三、教学反思
(你在本堂课中实施“四步”的体会)
A
C
A′
C′
B
B′
教学设计
一、教学背景与设计
学科
数学
所用教材
沪教版
任课教师
年级班级
课
题
11.1平移
本课教材分析
图形的运动是空间与图形领域中一块重要的内容。通过图形的运动使图形动起来,有助于在运动的过程中发现图形的变与不变性。因此,图形的运动是研究几何问题,发现结论的有效工具。而平移是沪教版七年级上册第十一章《图形的运动》第一节,引入平移运动,可以渗透图形的运动思想,使学生尽早尝试利用平移知识分析和解决问题。而本节主要讨论的是平移运动的基本性质,要求学生对平移有一个初步的认识。
课标要求及解读
了解平移的特征,能发现、归纳图形平移的特征。让学生经历观察、操作、探究、归纳等过程,总结平移的基本特征,进一步发展学生的抽象概括能力。让学生经历操作、实验、发现归纳等数学活动,感受数学活动的探索性和创造性。激发学生的探究人情,感受数学的美。
本课教学目标
1.在经历图形平移概念形成的过程中,培养数学语言概括能力,归纳出图形平移后图形的形状、大小保持不变的性质.2.知道对应点、对应角、对应线段的概念,并由概念得到平移的性质.3.会在方格纸上画出经过平移后的平面图形,初步体会图形运动.掌握平移方向的意义,会画出平移方向,量出平移距离.
学情分析
本节课采用的是开放式和探究式的教学方法,让学生通过探究,了解平移的特征,建构平移的概念,并采用多媒体辅助教学,演示平移变换的过程,激发学生的积极形,通过展示图片,体现数学的美的存在。
四步教学实施步骤
自学
(描述“自学”阶段你所设计的活动)通过微视频进行预学习并完成预学习单
交流
(描述“交流”阶段你所设计的活动)交流预学习知识并交流预学习留下的思考
指导
(描述“指导”阶段你所设计的活动)平移的性质以及平移中涉及的概念
反馈
(描述“反馈”阶段你所设计的活动)通过课堂练习反馈所学知识
教学重点
图形平移的性质
教学难点
图形平移的概念形成.
二、实施过程:
教师活动
学生活动
设计意图
一.自学师:在日常生活中我们会看到这样一些现象.请看大屏幕:课件演示直升飞机螺旋桨的运动、汽车在笔直的马路上行驶、蝴蝶翅膀的翻折运动.问:刚才我们看到了物体的有关运动,你能说出它们是什么运动吗?师:通过刚才的实例,如果我们把直升飞机螺旋桨、汽车、蝴蝶翅膀抽象成平面图形,这些实例就给我们以图形的三种基本运动形式的直观感受,在第十一章我们主要来学习平面中图形的运动.师:汽车在笔直马路上行驶实际上是物体的平移,若将地面看作平面,汽车看成是平面图形,那么就可以看作图形在平面中平移,那么图形究竟作怎样的运动才是平移呢?
思考:(1)从小船运动的现象中你发现小船运动的方向有什么特征吗?(2)如果在船头停着一只红鸟,船尾停着一只蓝鸟,当小船停靠岸时,两只小鸟发生了激烈的争吵.红鸟说:“我停在船头,经过的路长一点.”蓝鸟说:“不对不对,我停在船尾,经过的路长一点哩.”请同学们评评理,究竟谁经过的距离长一点?(3)如果小鸟停在船的如图所示的特殊的地方,而且小船沿着箭头所指的方向行驶,那么两只小鸟经过的距离又会怎样呢?
(4)将小鸟看作为一点,放在任意地方,如点P、点Q处,小鸟经过的距离又会怎样呢?你发现了什么规律?师:我们也可以得到,这个图形上所有的点都按照某个相同的方向作相同距离的位置移动.(5)小船在运动过程中什么发生了变化?(6)以上图形的在运动时有什么共同特征?
平移的概念:这种将图形上所有的点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移.图形平移的性质:图形平移后,图形的大小不变,图形的形状不变.问:在生活中,你能举出一些平移运动的实例吗?对应点、对应线段、对应角的概念:初始位置的图形与终止位置的图形叫做对应图形,其中,点A与点A′为对应点,线段AB与线段A′B′为对应线段,∠A与∠A′为对应角.图形平移后,图形的大小不变,图形的形状不变.问:你还能说出图中其他的对应点、对应线段、对应角吗?练习:如图,平移△ABC就可以得到△A′B′C′,点C的对应点为_________,线段AC的对应线段为_________,∠C的对应角为_________.二、交流例题1
画出△ABC向右平移4格,向下平移3格后的图形.问1:△ABC平移后所得的图形是什么?
问2:怎样画出平移后的三角形?为什么?解:(i)如图,分别画出点A、B、C向右平移4格,向下平移3格后所对应的点A1、B1、C1;(ii)联结A1B1、B1C1、A1C1,得△A1B1C1.△A1B1C就是所求作的图形.三、指导例题1
画出△ABC向右平移4格,向下平移3格后的图形.大屏幕播放:后面一个三角形是由前面的三角形平移得到的.请同学们拿出度量工具量一量:验证图形平移的性质图形平移的性质:1.图形平移后,对应点之间的距离相等、对应线段的长度、对应角的大小相等.2.图形平移后,图形的大小不变,图形的形状不变.平移的距离:平移后各对应点之间的距离叫做图形平移的距离.问:在练习题中,你能说出△ABC与到△A′B′C′平移的距离吗?为什么?问3:你能画出上图中△ABC平移的方向,并量出平移的距离吗?例2
如图把四边形向左平移4格,再向下平移2格,画出平移后的图形,并画出平移方向,量出平移的距离.问:此题需要分别画出几个点的对应点?【适时小结】1.要画出平移后的多边形的图形,关键在于找到这个多边形的各个顶点平移后的对应点的位置.2.平移方向与平移操作是不同的,平移操作仅限于在方格纸上将图形沿着水平方向或竖直方向做平移运动,平移方向只关注平移图形的初始位置.四、反馈课堂练习:1.平移改变的是图形的(
)A、形状
B、位置 C、大小 D、形状、大小及位置2.∠DEF是∠ABC经过平移得到的,如果∠ABC=45°,那么∠DEF的度数为
.为什么?3.在下面六幅图案中,图案(2)、(3)、(4)、(5)、(6)中的哪个图案可以通过平移图案(1)得到?4、如图,把箭头状图形向右平移4格,向下平移2格,画出平移后的图形.5、图中的四个小三角形都是边长为2cm的等边三角形,平移△ABC能与哪些三角形重合?6、有一块边长为101m的正方形稻田,,稻田里有纵横各两条水渠,渠宽都是0.5m,问稻田的种植面积是多少?五.课堂小结:本节课你有哪些收获与体会?
图形平移的概念.图形平移的性质.
直升飞机螺旋桨的运动:旋转汽车在笔直的马路上行驶:平移.蝴蝶翅膀的翻折:翻折.(1)小船按照从左到右的方向移动.(2)红鸟与蓝鸟经过的距离相等,都是7个单位.(3)两只小鸟经过的距离仍然相等.无论小鸟停在船的任何位置,它们移动的方向和距离都相等.(4)小鸟经过的距离仍然相等.无论小鸟停在船的任何位置,它们移动的距离都相等.(5)小船在运动过程中仅位置发生了改变.(6)图形上所有的点都按照某个方向作相同距离的位置移动.移门、电梯等.点B与点B′为对应点,线段BC与线段B′C′为对应线段,∠B与∠B′为对应角.点C的对应点为___C′___,线段AC的对应线段为A′C′,∠C的对应角为
∠C
__.问1:△ABC平移后所得的图形仍然是三角形.问2:由于图形经过平移运动后,图形上的任何一点平移的距离都相等,所以只需分别画出A、B、C三点平移后的对应点,再联结各点,就可以得到平移后的三角形.△ABC与到△A′B′C′平移的距离为对应点之间的距离相等,所以只需测量出两个三角形中的一个点与它的对应点之间的距离即可.平移的方向为射线A
A1或射线B
B1、CC1的方向.平移的距离为线段A
A1或线段B
B1、CC1的长度.B2.∠DEF=45°,图形平移后,对应角的大小相等.3.(3)5.平移△ABC能与△ECD、△FAE重合.6、解:(101-0.5×2)2=1002=10000m2答:稻田的种植面积是10000
m2.1.平移的概念:这种将图形上所有的点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移.2.图形平移的性质:(1)图形平移后,对应点之间的距离相等、对应线段的长度、对应角的大小相等.(2)图形平移后,图形的大小不变,图形的形状不变.
从现实生活中具体实例抽象出数学问题,感受图形的基本运动.根据生活中物体位移进一步抽象到平面中图形的平移,引导学生根据自己生活中已有的经验,形成图形平移的概念.如学生举出物体位移的实例,教师应帮助其将物体抽象为平面图形的平移运动.通过把小船抽象为几何图形,来给出对应点、对应线段、对应角的概念.让学生认识到,要画出平移后的三角形的图形,关键在于找到这个三角形的三个顶点(特殊点)平移后的对应点的位置.教师引导学生动手测量图形运动前后对应边的长度、对应角的大小及对应点之间的距离等,验证图形平移的性质.补充例2,画一个四边形平移后的图形,让学生进一步理解画平移后的图形关键在于找到这个多边形的各个顶点平移后的对应点的位置.巩固新知,运用新知,突出重点,反馈调控.
梳理本节课知识,教师进一步提炼总结,提升学生的认识水平.
三、教学反思
(你在本堂课中实施“四步”的体会)
A
C
A′
C′
B
B′
