沪教版(上海)数学八年级第二学期-22.3 特殊的平行四边形 教案
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.3 特殊的平行四边形 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 64.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
22.3
特殊的平行四边形
执教者:
教学目标:
1、
尝试通过练习,梳理特殊平行四边形的性质与判定,使所学知识系统化,网络化
2、学会利用特殊平行四边形的知识解决简单的具体问题,提高分析问题,解决问题的能力
3、经历知识的归纳与整理的过程,养成反思与梳理知识的习惯和能力
教学重点:
梳理平行四边形的知识结构体系,根据具体问题情境,选择适当的知识进行推理计算,并解决问题。教学难点:
平行四边形、矩形、菱形、正方形的性质和判定的灵活运用
教材分析:
四边形和三角形一样,是基本的平面图形,是空间与图形部分的重要组成部分,平行四边形、菱形、矩形、正方形之间的区别与联系对灵活的掌握及运用四边形的知识起着重要的作用。特殊平行四边形概念、性质与判定是学好本章的关键,也是为学好整个平面几何打下一个坚实的基础,是本章的教学重点。本节课的目的就是通过一组基础练习与综合运用,的训练,掌握平行四边形、菱形、矩形、正方形之间的联系及区别。
学情分析:
八年级的学生,经过两年实验几何的学习、近一年论证几何的探索,学生已基本掌握了平行、垂直、相交、三角形等相关知识,并且有了一定的说理能力,经过本章前一部分的学习,学生已经基本掌握了平行四边形、菱形、矩形、正方形的性质及它们的判定,但是在学习平行四边形、菱形、矩形和正方形时,知识都相对比较独立,学生对这些特殊的平行四边形之间的关系掌握得还不是很好,比较陌生。
设计思路:
教学设计了课前任务环节,利用网络工具,及时反馈学生存在问题,并根据问题设计本课时重点突破内容。由浅入深,由两个基础问题入手,唤醒学生的特殊四边形知识,同时做了适当的变式训练让学生理清本单元知识,理解各知识点的作用和联系,
教学过程:
教学环节
教学活动
设计意图
课前任务反馈
任务反馈完成课前练习与分析,结果统计于屏幕
通过课前任务,将学习空间与时间前置,梳理平行四边形,矩形,菱形,正方形之间的联系和区别
基础问题引入
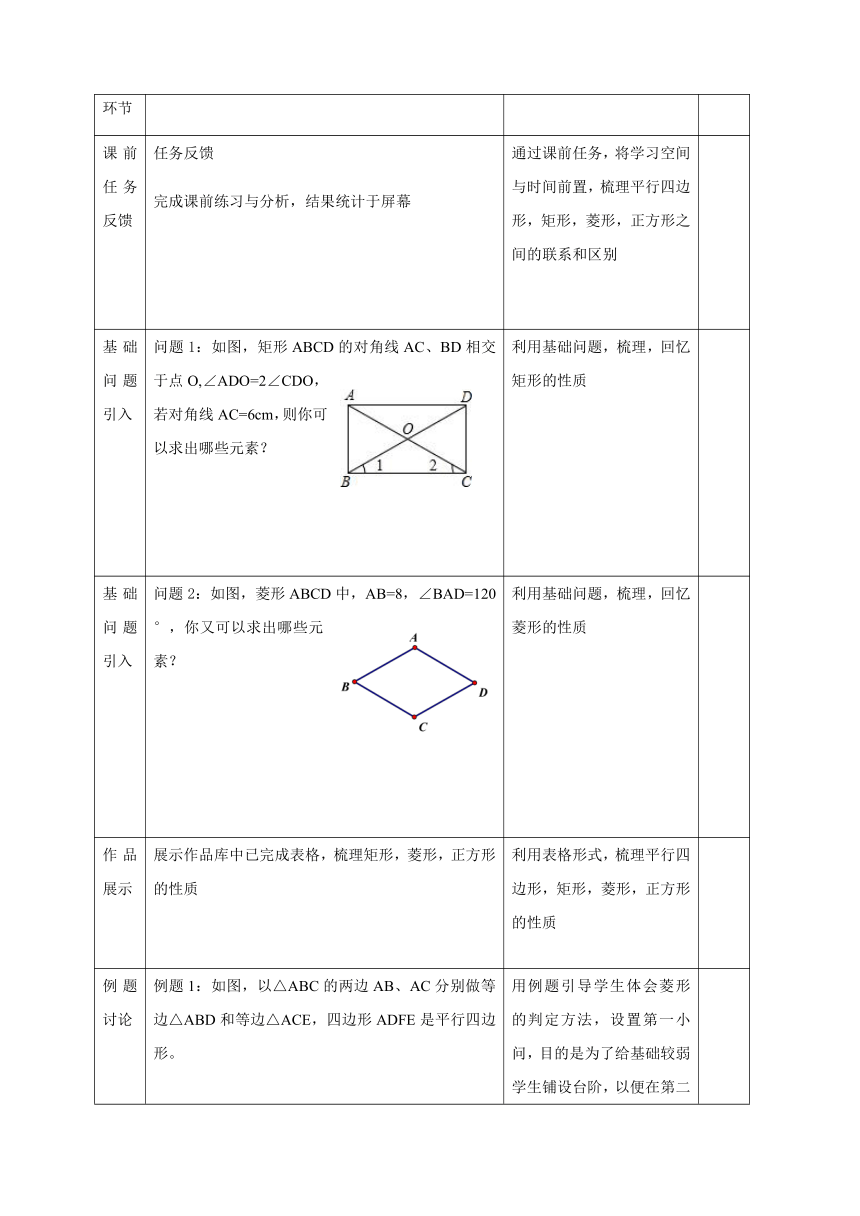
问题1:如图,矩形ABCD的对角线AC、BD相交于点O,∠ADO=2∠CDO,若对角线AC=6cm,则你可以求出哪些元素?
利用基础问题,梳理,回忆矩形的性质
基础问题引入
问题2:如图,菱形ABCD中,AB=8,∠BAD=120°,你又可以求出哪些元素?
利用基础问题,梳理,回忆菱形的性质
作品展示
展示作品库中已完成表格,梳理矩形,菱形,正方形的性质
利用表格形式,梳理平行四边形,矩形,菱形,正方形的性质
例题讨论
例题1:如图,以△ABC的两边AB、AC分别做等边△ABD和等边△ACE,四边形ADFE是平行四边形。(1)当∠ABC=_______时,平行四边形ADFE不存在(2)当△ABC满足__________条件时,平行四边形ADFE是菱形?
用例题引导学生体会菱形的判定方法,设置第一小问,目的是为了给基础较弱学生铺设台阶,以便在第二小题中,不遗漏∠ABC≠60°的情况
复习菱形判定
例题2:如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD,请判断四边形OCED的形状,并说明理由。例题2变式:如图,O为矩形ABCD对角线的交点,E是CD中点,联结OE,过点C作CF∥BD交线段OE的延长线与点F,联结DF,求证:(1)△ODE≌△FCE(2)四边形ODFC是菱形
及时利用例题解决,复习菱形的判定方法,并利用变式,让学生体会特殊的平行四边形的性质与判定的综合运用。
复习矩形与正方形判定
例题1:如图,以△ABC的两边AB、AC分别做等边△ABD和等边△ACE,四边形ADFE是平行四边形。(3)当△ABC满足__________条件时,平行四边形ADFE是矩形?(4)当△ABC满足__________条件时,平行四边形ADFE是正方形?
用已有例题引导学生体会矩形和正方形的判定方法,利用分析过的熟悉图形,降低分析难度,提高效率
构建知识网络
例题3:如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
通过简单问题的解决,复习特殊四边形判定方法,初步形成判定特殊四边形知识网络。
综合运用与提高
例题3变式:如图,在△ABC中,点O是AC边上的一个动点,(不与A、C重合),过点O作直线MN∥BC,直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F(1)OE与OF相等吗?为什么?(2)当点O运动到何处时,四边形AECF是矩形?(3)当△ABC是什么三角形时,四边形AECF为正方形?
逐步引导学生如何应用知识进行分析,分析已知中的条件,分析结论中的信息,训练性质和判定的综合运用。
小结提高
通过今天的学习,学习到了哪些特殊的平行四边形判定的路径?
课堂检测
推送检测习题,并及时反馈习题附后
通过电子书包推送练习,并及时反馈问题与正确率
投票
小组争章投票,选出优秀小组
特殊的平行四边形
执教者:
教学目标:
1、
尝试通过练习,梳理特殊平行四边形的性质与判定,使所学知识系统化,网络化
2、学会利用特殊平行四边形的知识解决简单的具体问题,提高分析问题,解决问题的能力
3、经历知识的归纳与整理的过程,养成反思与梳理知识的习惯和能力
教学重点:
梳理平行四边形的知识结构体系,根据具体问题情境,选择适当的知识进行推理计算,并解决问题。教学难点:
平行四边形、矩形、菱形、正方形的性质和判定的灵活运用
教材分析:
四边形和三角形一样,是基本的平面图形,是空间与图形部分的重要组成部分,平行四边形、菱形、矩形、正方形之间的区别与联系对灵活的掌握及运用四边形的知识起着重要的作用。特殊平行四边形概念、性质与判定是学好本章的关键,也是为学好整个平面几何打下一个坚实的基础,是本章的教学重点。本节课的目的就是通过一组基础练习与综合运用,的训练,掌握平行四边形、菱形、矩形、正方形之间的联系及区别。
学情分析:
八年级的学生,经过两年实验几何的学习、近一年论证几何的探索,学生已基本掌握了平行、垂直、相交、三角形等相关知识,并且有了一定的说理能力,经过本章前一部分的学习,学生已经基本掌握了平行四边形、菱形、矩形、正方形的性质及它们的判定,但是在学习平行四边形、菱形、矩形和正方形时,知识都相对比较独立,学生对这些特殊的平行四边形之间的关系掌握得还不是很好,比较陌生。
设计思路:
教学设计了课前任务环节,利用网络工具,及时反馈学生存在问题,并根据问题设计本课时重点突破内容。由浅入深,由两个基础问题入手,唤醒学生的特殊四边形知识,同时做了适当的变式训练让学生理清本单元知识,理解各知识点的作用和联系,
教学过程:
教学环节
教学活动
设计意图
课前任务反馈
任务反馈完成课前练习与分析,结果统计于屏幕
通过课前任务,将学习空间与时间前置,梳理平行四边形,矩形,菱形,正方形之间的联系和区别
基础问题引入
问题1:如图,矩形ABCD的对角线AC、BD相交于点O,∠ADO=2∠CDO,若对角线AC=6cm,则你可以求出哪些元素?
利用基础问题,梳理,回忆矩形的性质
基础问题引入
问题2:如图,菱形ABCD中,AB=8,∠BAD=120°,你又可以求出哪些元素?
利用基础问题,梳理,回忆菱形的性质
作品展示
展示作品库中已完成表格,梳理矩形,菱形,正方形的性质
利用表格形式,梳理平行四边形,矩形,菱形,正方形的性质
例题讨论
例题1:如图,以△ABC的两边AB、AC分别做等边△ABD和等边△ACE,四边形ADFE是平行四边形。(1)当∠ABC=_______时,平行四边形ADFE不存在(2)当△ABC满足__________条件时,平行四边形ADFE是菱形?
用例题引导学生体会菱形的判定方法,设置第一小问,目的是为了给基础较弱学生铺设台阶,以便在第二小题中,不遗漏∠ABC≠60°的情况
复习菱形判定
例题2:如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD,请判断四边形OCED的形状,并说明理由。例题2变式:如图,O为矩形ABCD对角线的交点,E是CD中点,联结OE,过点C作CF∥BD交线段OE的延长线与点F,联结DF,求证:(1)△ODE≌△FCE(2)四边形ODFC是菱形
及时利用例题解决,复习菱形的判定方法,并利用变式,让学生体会特殊的平行四边形的性质与判定的综合运用。
复习矩形与正方形判定
例题1:如图,以△ABC的两边AB、AC分别做等边△ABD和等边△ACE,四边形ADFE是平行四边形。(3)当△ABC满足__________条件时,平行四边形ADFE是矩形?(4)当△ABC满足__________条件时,平行四边形ADFE是正方形?
用已有例题引导学生体会矩形和正方形的判定方法,利用分析过的熟悉图形,降低分析难度,提高效率
构建知识网络
例题3:如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:AB=CF;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
通过简单问题的解决,复习特殊四边形判定方法,初步形成判定特殊四边形知识网络。
综合运用与提高
例题3变式:如图,在△ABC中,点O是AC边上的一个动点,(不与A、C重合),过点O作直线MN∥BC,直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F(1)OE与OF相等吗?为什么?(2)当点O运动到何处时,四边形AECF是矩形?(3)当△ABC是什么三角形时,四边形AECF为正方形?
逐步引导学生如何应用知识进行分析,分析已知中的条件,分析结论中的信息,训练性质和判定的综合运用。
小结提高
通过今天的学习,学习到了哪些特殊的平行四边形判定的路径?
课堂检测
推送检测习题,并及时反馈习题附后
通过电子书包推送练习,并及时反馈问题与正确率
投票
小组争章投票,选出优秀小组
