人教版数学八年级上册 12.1全等三角形基础检测 (word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 12.1全等三角形基础检测 (word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 392.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 21:46:55 | ||
图片预览




文档简介
人教版数学八年级上册
第12章
基础检测含答案
12.1全等三角形
一.选择题
1.已知△ABC的三边的长分别为3,5,7,△DEF的三边的长分别为3,7,2x﹣1,若这两个三角形全等,则x的值是( )
A.3
B.5
C.﹣3
D.﹣5
2.如图,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.∠ABD=∠CBD
B.△ABD和△CDB的周长相等
C.AD=BC
D.△ABD和△CDB的面积相等
3.如图两个直角三角形,若△ABC≌△CDE,则线段AC和线段CE的关系是( )
A.既不相等也不互相垂直
B.相等但不互相垂直
C.互相垂直但不相等
D.相等且互相垂直
4.如图,△ABC与△DEF是全等三角形,则图中相等的线段有( )
A.1对
B.2对
C.3对
D.4对
5.△ABC≌△DEF,AB=2,BC=4,若△DEF的周长为偶数,则DF的取值为( )
A.3
B.4
C.5
D.3或4或5
6.下列说法正确的是( )
A.面积相等的两个图形全等
B.周长相等的两个图形全等
C.形状相同的两个图形全等
D.全等图形的形状和大小相同
7.已知△ABC≌△FED,若∠E=37°,∠C=100°,则∠A的度数是( )
A.100°
B.80°
C.43°
D.37°
8.如图,△ABC≌△DEF,∠A=50°,∠C=30°,则∠E的度数为( )
A.30°
B.50°
C.60°
D.100°
9.下列各组图形中,是全等形的是( )
A.两个含60°角的直角三角形
B.腰对应相等的两个等腰直角三角形
C.边长为3和4的两个等腰三角形
D.一个钝角相等的两个等腰三角形
10.已知,如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是( )
A.AC=DF
B.AD=BE
C.DF=EF
D.BC=EF
二.填空题
11.已知△ABC≌△DEF,BC=EF=6厘米,△ABC的面积为9平方厘米,则EF边上的高是
厘米.
12.在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标
.
13.如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC=
.
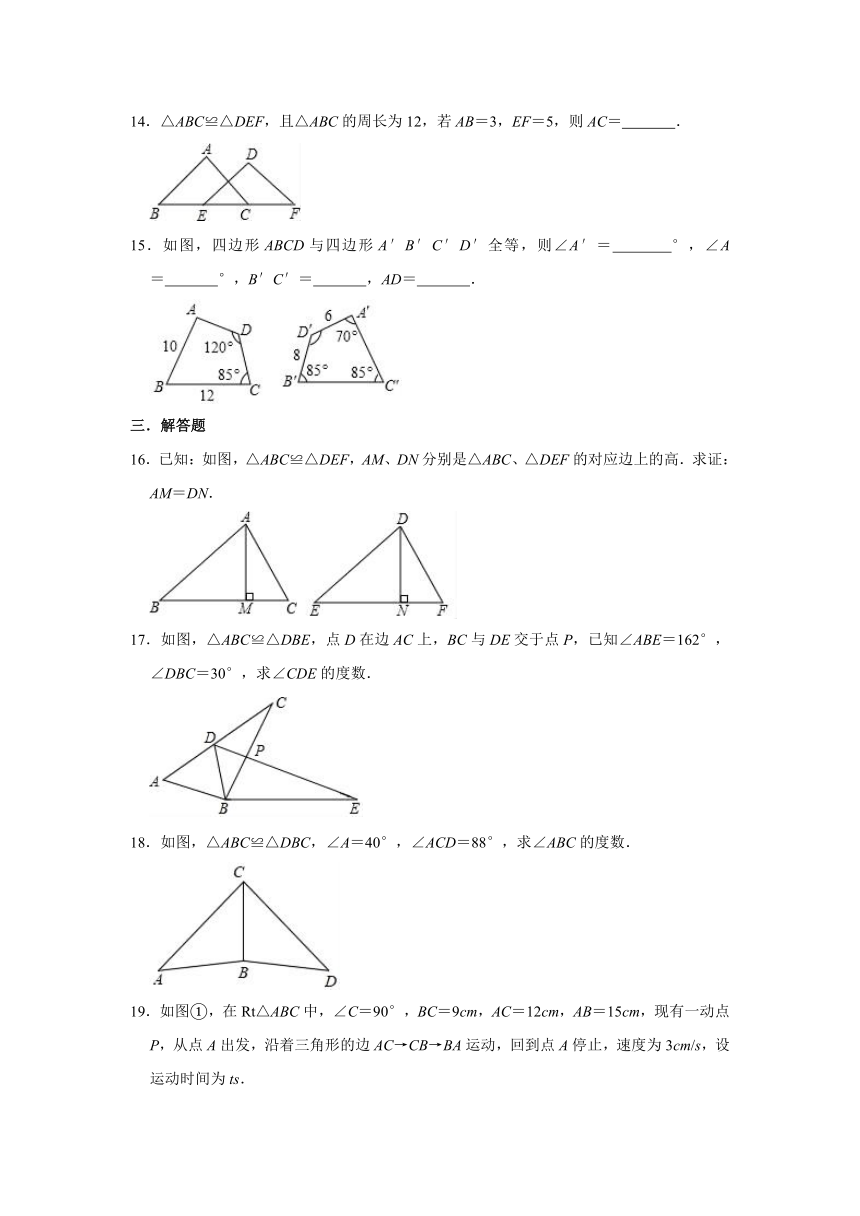
14.△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=5,则AC=
.
15.如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=
°,∠A=
°,B′C′=
,AD=
.
三.解答题
16.已知:如图,△ABC≌△DEF,AM、DN分别是△ABC、△DEF的对应边上的高.求证:AM=DN.
17.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
18.如图,△ABC≌△DBC,∠A=40°,∠ACD=88°,求∠ABC的度数.
19.如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图(1),当t=
时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
参考答案与试题解析
一.选择题
1.【解答】解:∵这两个三角形全等,
∴2x﹣1=5,
解得,x=3,
故选:A.
2.【解答】解:A、∵△ABD≌△CDB,∴∠ABD=∠CBD,选项说法错误;
B、∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,选项说法正确;
C、∵△ABD≌△CDB,∴AD=BC,选项说法正确;
D、∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,选项说法正确;
故选:A.
3.【解答】解:∵Rt△ABC≌Rt△CDE,
∴AC=CE,∠A=∠ECD,∠B=∠D,∠ACB=∠E.
∵△ABC是直角三角形,
∠A+∠ACB=90°,
∴∠ACB+∠ECD=∠ACB+∠A=90°,
∴∠ACE=180°﹣90°=90°,
∴AC⊥CE,
∴AC和CE相等且互相垂直,
故选:D.
4.【解答】解:∵△ABC与△DEF是全等三角形,
∴AB=DE,AC=DF,BC=EF,
∴BC﹣EC=EF﹣EC,
∴BE=CF,
即相等的线段有4对,
故选:D.
5.【解答】
解:∵△ABC≌△DEF,AB=2,BC=4,
∴DE=AB=2,EF=BC=4,
∴4﹣2<DF<4+2,
∴2<DF<6,
∵DE=2,EF=4,△DEF的周长为偶数,
∴DF=4,
故选:B.
6.【解答】解:A、面积相等的两个图形全等,说法错误;
B、周长相等的两个图形全等,说法错误;
C、形状相同的两个图形全等,说法错误;
D、全等图形的形状和大小相同,说法正确;
故选:D.
7.【解答】解:∵△ABC≌△FED,∠E=37°,
∴∠B=∠E=37°,
∵∠C=100°,
∴∠A=180°﹣∠B﹣∠C=180°﹣37°﹣100°=43°,
故选:C.
8.【解答】解:∵△ABC≌△DEF,∠A=50°,∠C=30°,
∴∠F=∠C=30°,∠D=∠A=50°,
∴∠E=180°﹣∠D﹣∠F=180°﹣50°﹣30°=100°,
故选:D.
9.【解答】解:A、两个含60°角的直角三角形,缺少对应边相等,所以不是全等形;
B、腰对应相等的两个等腰直角三角形,符合AAS或ASA,或SAS,是全等形;
C、边长为3和4的两个等腰三角形有可能是3,3,4或4,4,3不一定全等对应关系不明确不一定全等;
D、一个钝角相等的两个等腰三角形.缺少对应边相等,不是全等形.
故选:B.
10.【解答】解:A、∵△ABC≌△DEF,∴AC=DF,故此结论正确;
B、∵△ABC≌△DEF,∴AB=DE;∵DB是公共边,∴AB﹣BD=DE﹣BD,即AD=BE;故此结论正确;
C、∵△ABC≌△DEF,∴AC=DF,故此结论DF=EF错误;
D、∵△ABC≌△DEF,∴BC=EF,故此结论正确;
故选:C.
二.填空题(共5小题)
11.【解答】解:设△ABC边BC上的高为h,
则△ABC的面积=BCh=×6h=9,
解得h=3,
∵△ABC≌△DEF,BC=EF,
∴EF边上的高是3cm.
故答案为:3.
12.【解答】解:如图所示:有3个点,当E在E、F、N处时,△ACE和△ACB全等,
点E的坐标是:(1,5),(1,﹣1),(5,﹣1),
故答案为:(1,5)或(1,﹣1)或(5,﹣1).
13.【解答】解:∵∠BAE=120°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=120°﹣40°=80°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE=80°.
故答案为:80°.
14.【解答】解:∵△ABC≌△DEF,EF=5,
∴BC=EF=5,
∵△ABC的周长为12,AB=3,
∴AC=12﹣5﹣3=4.
故答案为:4.
15.【解答】解:由题意得:∠A′=70°,∠A=∠A′=70°,B′C′=BC=12,AD=A′D′=6.
故答案为:70°,70°,12,6.
三.解答题(共4小题)
16.【解答】方法一:
证明:∵△ABC≌△DEF,
∴AB=DE,∠B=∠E,
∵AM,DN分别是△ABC,△DEF的对应边上的高,
即AM⊥BC,DN⊥EF,
∴∠AMB=∠DNE=90°,
在△ABM和△DEN中,
∴△ABM≌△DEN(AAS),
∴AM=DN.
方法二:
∵△ABC≌△DEF,
∴BC=EF,
∵AM、DN分别是△ABC、△DEF的对应边上的高,
∴BCAM=EFDN,
∴AM=DN.
17.【解答】解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
18.【解答】解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°﹣40°﹣44°=96°.
19.【解答】解:(1)①当点P在BC上时,如图①﹣1,
若△APC的面积等于△ABC面积的一半;则CP=BC=cm,
此时,点P移动的距离为AC+CP=12+=,
移动的时间为:÷3=秒,
②当点P在BA上时,如图①﹣2
若△APC的面积等于△ABC面积的一半;则PD=BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+=cm,
移动的时间为:÷3=秒,
故答案为:或;
(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;
①当点P在AC上,如图②﹣1所示:
此时,AP=4,AQ=5,
∴点Q移动的速度为5÷(4÷3)=cm/s,
②当点P在AB上,如图②﹣2所示:
此时,AP=4,AQ=5,
即,点P移动的距离为9+12+15﹣4=32cm,点Q移动的距离为9+12+15﹣5=31cm,
∴点Q移动的速度为31÷(32÷3)=cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,
点Q的运动速为cm/s或cm/s
12.2三角形全等的判定
一.选择题
1.如图,在△ABC中,AB=AC,E、D分别为AB、AC边上的中点,连接BD、CE交于O,此图中全等三角形的对数为( )对.
A.4
B.3
C.2
D.1
2.如图,AB=AD,∠1=∠2,则不一定使△ABC≌△ADE的条件是( )
A.∠B=∠D
B.∠C=∠E
C.BC=DE
D.AC=AE
3.如图,A、B、C、D在一条直线上,MB=ND,∠MBA=∠D,添加下列某一条件后不能判定△ABM≌△CDN的是( )
A.∠M=∠N
B.AB=CD
C.AM=CN
D.AM∥CN
4.根据下列已知条件,能够画出唯一△ABC的是( )
A.AB=6,BC=5,∠A=50°
B.AB=5,BC=6,AC=13
C.∠A=50°,∠B=80°,AB=8
D.∠A=40°,∠B=50°,∠C=90°
5.如图,AD为∠BAC的平分线,添加下列条件后,不能证明△ABD≌△ACD的是( )
A.∠B=∠C
B.∠BDA=∠CDA
C.BD=CD
D.AB=AC
6.如图,给出的四组条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,BC=EF,AC=DF
B.AB=DE,∠B=∠E,BC=EF
C.AB=DE,AC=DF,∠B=∠E
D.∠B=∠E,BC=EF,∠C=∠F.
7.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS
B.SAS
C.ASA
D.SSS
8.如图,要测量河两岸相对两点A、B间的距离,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
A.SAS
B.SSS
C.ASA
D.AAS
9.如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
10.在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A',⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是( )
A.①②③
B.①②⑤
C.①②④
D.②⑤⑥
二.填空题
11.△ABC中,AB=5,AC=a,BC边上的中线AD=4,则a的取值范围是
.
12.如图,已知CA=DB,要使△ABC和△ABD全等,请补充条件
(填上一种即可).
13.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=
.
14.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:
①△ABD≌△EBC;
②∠BCE+∠BCD=180°;
③AF2=EC2﹣EF2;
④BA+BC=2BF.
其中正确的是
.
15.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则m+n
b+c.
三.解答题
16.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
17.已知:如图,E在△ABC的边AC上,且∠AEB=∠ABC.
(1)求证:∠ABE=∠C;
(2)若∠BAE的平分线AF交BE于点F,FD∥BC交AC于点D,设AB=8,AC=10,求DC的长.
18.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=2,求△ABC的周长.
19.已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
参考答案与试题解析
一.选择题
1.【解答】解:∵AB=AC,
∴∠EBC=∠DCB,
∵AE=BE,AD=DC,
∴BE=DC,∵BC=CB,
∴△EBC≌△DCB,
∴∠ECB=∠DBC,
∴∠EBO=∠DCO,
∵BE=CD,∴∠BOE=∠COD,
∴△BOE≌△COD,
∵∠A=∠A,AB=AC,∠ABD=∠ACE,
∴△ABD≌△ACE,
共有3对全等三角形,
故选:B.
2.【解答】解:∵∠1=∠2,
∵∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
A、符合ASA定理,即能推出△ABC≌△ADE,故本选项错误;
B、符合AAS定理,即能推出△ABC≌△ADE,故本选项错误;
C、不符合全等三角形的判定定理,即不能推出△ABC≌△ADE,故本选项正确;
D、符合SAS定理,即能推出△ABC≌△ADE,故本选项错误;
故选:C.
3.【解答】解:A、根据ASA可以判定△ABM≌△CDN;
B、根据SAS可以判定△ABM≌△CDN;
C、SSA无法判定三角形全等;
D、根据AAS即可判定△ABM≌△CDN;
故选:C.
4.【解答】解:A、已知AB、BC和BC的对角,不能画出唯一三角形,故本选项错误;
B、∵AB+BC=5+6=11<AC,
∴不能画出△ABC;
故本选项错误;
C、已知两角和夹边,能画出唯一△ABC,故本选项正确;
D、根据∠A=40°,∠B=50°,∠C=90°不能画出唯一三角形,故本选项错误;
故选:C.
5.【解答】解:A、由,可得到△ABD≌△ACD,所以A选项不正确;
B、由,可得到△ABD≌△ACD,所以B选项不正确;
C、由BD=CD,AD=AD,∠BAD=∠CAD,不能得到△ABD≌△ACD,所以C选项正确.
D、由,可得到△ABD≌△ACD,所以D选项不正确;
故选:C.
6.【解答】解:A、由全等三角形的判定定理SSS能证明△ABC≌DEF,故此选项错误;
B、由全等三角形的判定定理SAS能证明△ABC≌DEF,故此选项错误;
C、由SSA不能证明△ABC≌DEF,故此选项正确;
D、由全等三角形的判定定理ASA能证明△ABC≌DEF,故此选项错误;
故选:C.
7.【解答】解:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
在△ACB和△ACD中,
,
∴△ACB≌△ACD(SAS),
∴AB=AD(全等三角形的对应边相等).
故选:B.
8.【解答】解:∵AB⊥BD,ED⊥BD,
∴∠ABD=∠EDC=90°,
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA)
故选:C.
9.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
10.【解答】解:∵在△ABC和△A′B′C′中,有边边角、角角角不能判定三角形全等,
∴①②④是边边角,
∴不能保证△ABC≌△A′B′C′.
故选:C.
二.填空题(共5小题)
11.【解答】解:延长AD到E,使AD=DE,连接BE,
∵AD=DE,∠ADC=∠BDE,BD=DC,
∴△ADC≌△EDB(SAS)
∴BE=AC=a,
在△AEB中,AB﹣BE<AE<AB+BE,
即5﹣a<2AD<5+a,
∴<AD<.,
∵AD=4,
∴a的取值范围是3<a<13,
故答案为:3<a<13
12.【解答】解:当CB=DA时,△ABC≌△ABD,
在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS),
故答案为:CB=DA.
13.【解答】解:∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴AC=DF=5(全等三角形对应边相等).
故答案为:5.
14.【解答】解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS),
∴①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,
∴②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
∵EF⊥AB,
∴AF2=EC2﹣EF2;
∴③正确;
④如图,过E作EG⊥BC于G点,
∵E是BD上的点,∴EF=EG,
在Rt△BEG和Rt△BEF中,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
,
∴Rt△CEG≌Rt△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF,
∴④正确.
故答案为:①②③④.
15.【解答】解:如图,在BA的延长线上取点E,使AE=AC,连接EP,
∵AD是∠A的外角平分线,
∴∠CAD=∠EAD,
在△ACP和△AEP中,
,
∴△ACP≌△AEP(SAS),
∴PE=PC,
在△PBE中,PB+PE>AB+AE,
∵PB=m,PC=n,AB=c,AC=b,
∴m+n>b+c.
故答案为:>.
三.解答题(共4小题)
16.【解答】(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
17.【解答】(1)证明:在△ABE中,∠ABE=180°﹣∠BAE﹣∠AEB,
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC,
∵∠AEB=∠ABC,∠BAE=∠BAC,
∴∠ABE=∠C;
(2)解:∵FD∥BC,
∴∠ADF=∠C,
又∠ABE=∠C,
∴∠ABE=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠DAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS),
∴AB=AD,
∵AB=8,AC=10,
∴DC=AC﹣AD=AC﹣AB=10﹣8=2.
18.【解答】(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠B=∠C(等边对等角).
∵D是BC的中点,
∴BD=CD.
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS).
∴DE=DF
(2)解:∵AB=AC,∠A=60°,
∴△ABC为等边三角形.
∴∠B=60°,
∵∠BED=90°,
∴∠BDE=30°,
∴BE=BD,
∵BE=2,
∴BD=4,
∴BC=2BD=8,
∴△ABC的周长为24.
19.【解答】解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=ABC,∠ECB=ACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠BAC)=90°∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
12.3《角平分线性质》
、选择题
如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于(
)
A.25°
B.30°
C.35°
D.40°
如图,已知∠AOB.
按照以下步骤作图:
①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD.
②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,
连接CE,DE.
③连接OE交CD于点M.
下列结论中错误的是( )
A.∠CEO=∠DEO
B.CM=MD
C.∠OCD=∠ECD
D.S四边形OCED=CD?OE
如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于(
)
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若BC=7,则AE的长为( )
A.4
B.5
C.6
D.7
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有(
)
A.4个
B.3个
C.2个
D.1个
如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=(
)
A.
6
B.
3
C.
2
D.
1.5
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长是(
)
A.6cm
B.4cm
C.10cm
D.以上都不对
如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是(
)
A.PM>PN
B.PM<PN
C.PM=PN
D.不能确定
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为(
)
A.25°
B.30°
C.35°
D.40°
如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是(
)
A.56°
B.60°
C.68°
D.94°
如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是(
)
A.∠C=∠ABC
B.BA=BG
C.AE=CE
D.AF=FD
如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.
下列结论:
①∠ABE=∠ACE;②∠BCE+∠BCD=180°;③AE=EC;④BE+BD=2BF,其中正确的是( )
A.①②③
B.①③④
C.①②④
D.①②③④
、填空题
如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,AC=8cm,AE=4cm,则DE的长是 .
如图,AD是△ABC的角平分线,DE⊥AB于E,若AB=18,AC=12,△ABC的面积等于36,则DE= .
若△ABC的周长为41
cm,边BC=17
cm,ABcm.
.如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,∠BOC=
.
如图所示,已知△ABC的周长是18,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 .
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为?
???.
、解答题
如图所示,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD,求证:∠C=2∠B.
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC.
求证:∠A+∠C=180°.
(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
①
求证:OE=BE;
②
若△ABC
的周长是25,BC=9,试求出△AEF的周长;
(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,试探求∠BAC
与∠PAC的数量关系式.
参考答案
D
答案为:C.
C
D
答案为:A;
答案为:D;
A.
C
C
A
B
答案为:D.
答案为:3cm.
答案为:2.4.
答案为:9;
答案为:125°.
答案为:36.
答案为:6;
证明:连接AD,
在△ACD和△ABD中,,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
证明:(1)过O点作OE⊥AC于点E.
∵∠ABD=90°且OA平分∠BAC
∴OB=OE,
又∵O是BD中点
∴OB=OD,
∴OE=OD,
∵OE⊥AC,∠D=90°
∴点O在∠ACD
的角平分线上
∴OC平分∠ACD.
(2)在Rt△ABO和Rt△AEO中
∵
∴Rt△ABO≌Rt△AEO(HL),
∴AB=AE,
在Rt△CDO和Rt△CEO中
∵
∴Rt△CDO≌Rt△CEO(HL),
∴CD=CE,
∴AB+CD=AE+CE=AC.
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
证明:延长AC至E,使CE=CD,连接ED
∵AB=AC+CD
∴AE=AB
∵AD平分∠CAB
∴∠EAD=∠BAD
∴AE=AB,∠EAD=∠BAD,AD=AD
∴△ADE≌△ADB
∴∠E=∠B且∠ACD=∠E+∠CDE,CE=CD
∴∠ACD=∠E+∠CDE=2∠E=2∠B
即∠C=2∠B
证明:过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F,
∵BD平分∠ABC,
∴DE=DF,∠DEC=∠F=90°,
在RtCDE和Rt△ADF中,
,
∴Rt△CDE≌Rt△ADF(HL),
∴∠FAD=∠C,
∴∠BAD+∠C=∠BAD+∠FAD=180°.
(1)∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EDB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE
(2)△AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25-9=16
(3)延长BA,证明P点在∠BAC外角的角平分线上,
从而得到2∠PAC+∠BAC=180°
第12章
基础检测含答案
12.1全等三角形
一.选择题
1.已知△ABC的三边的长分别为3,5,7,△DEF的三边的长分别为3,7,2x﹣1,若这两个三角形全等,则x的值是( )
A.3
B.5
C.﹣3
D.﹣5
2.如图,△ABD≌△CDB,下面四个结论中,不正确的是( )
A.∠ABD=∠CBD
B.△ABD和△CDB的周长相等
C.AD=BC
D.△ABD和△CDB的面积相等
3.如图两个直角三角形,若△ABC≌△CDE,则线段AC和线段CE的关系是( )
A.既不相等也不互相垂直
B.相等但不互相垂直
C.互相垂直但不相等
D.相等且互相垂直
4.如图,△ABC与△DEF是全等三角形,则图中相等的线段有( )
A.1对
B.2对
C.3对
D.4对
5.△ABC≌△DEF,AB=2,BC=4,若△DEF的周长为偶数,则DF的取值为( )
A.3
B.4
C.5
D.3或4或5
6.下列说法正确的是( )
A.面积相等的两个图形全等
B.周长相等的两个图形全等
C.形状相同的两个图形全等
D.全等图形的形状和大小相同
7.已知△ABC≌△FED,若∠E=37°,∠C=100°,则∠A的度数是( )
A.100°
B.80°
C.43°
D.37°
8.如图,△ABC≌△DEF,∠A=50°,∠C=30°,则∠E的度数为( )
A.30°
B.50°
C.60°
D.100°
9.下列各组图形中,是全等形的是( )
A.两个含60°角的直角三角形
B.腰对应相等的两个等腰直角三角形
C.边长为3和4的两个等腰三角形
D.一个钝角相等的两个等腰三角形
10.已知,如图,△ABC≌△DEF,AC∥DF,BC∥EF.则不正确的等式是( )
A.AC=DF
B.AD=BE
C.DF=EF
D.BC=EF
二.填空题
11.已知△ABC≌△DEF,BC=EF=6厘米,△ABC的面积为9平方厘米,则EF边上的高是
厘米.
12.在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标
.
13.如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC=
.
14.△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=5,则AC=
.
15.如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=
°,∠A=
°,B′C′=
,AD=
.
三.解答题
16.已知:如图,△ABC≌△DEF,AM、DN分别是△ABC、△DEF的对应边上的高.求证:AM=DN.
17.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
18.如图,△ABC≌△DBC,∠A=40°,∠ACD=88°,求∠ABC的度数.
19.如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(1)如图(1),当t=
时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.
参考答案与试题解析
一.选择题
1.【解答】解:∵这两个三角形全等,
∴2x﹣1=5,
解得,x=3,
故选:A.
2.【解答】解:A、∵△ABD≌△CDB,∴∠ABD=∠CBD,选项说法错误;
B、∵△ABD≌△CDB,
∴△ABD和△CDB的周长相等,选项说法正确;
C、∵△ABD≌△CDB,∴AD=BC,选项说法正确;
D、∵△ABD≌△CDB,
∴△ABD和△CDB的面积相等,选项说法正确;
故选:A.
3.【解答】解:∵Rt△ABC≌Rt△CDE,
∴AC=CE,∠A=∠ECD,∠B=∠D,∠ACB=∠E.
∵△ABC是直角三角形,
∠A+∠ACB=90°,
∴∠ACB+∠ECD=∠ACB+∠A=90°,
∴∠ACE=180°﹣90°=90°,
∴AC⊥CE,
∴AC和CE相等且互相垂直,
故选:D.
4.【解答】解:∵△ABC与△DEF是全等三角形,
∴AB=DE,AC=DF,BC=EF,
∴BC﹣EC=EF﹣EC,
∴BE=CF,
即相等的线段有4对,
故选:D.
5.【解答】
解:∵△ABC≌△DEF,AB=2,BC=4,
∴DE=AB=2,EF=BC=4,
∴4﹣2<DF<4+2,
∴2<DF<6,
∵DE=2,EF=4,△DEF的周长为偶数,
∴DF=4,
故选:B.
6.【解答】解:A、面积相等的两个图形全等,说法错误;
B、周长相等的两个图形全等,说法错误;
C、形状相同的两个图形全等,说法错误;
D、全等图形的形状和大小相同,说法正确;
故选:D.
7.【解答】解:∵△ABC≌△FED,∠E=37°,
∴∠B=∠E=37°,
∵∠C=100°,
∴∠A=180°﹣∠B﹣∠C=180°﹣37°﹣100°=43°,
故选:C.
8.【解答】解:∵△ABC≌△DEF,∠A=50°,∠C=30°,
∴∠F=∠C=30°,∠D=∠A=50°,
∴∠E=180°﹣∠D﹣∠F=180°﹣50°﹣30°=100°,
故选:D.
9.【解答】解:A、两个含60°角的直角三角形,缺少对应边相等,所以不是全等形;
B、腰对应相等的两个等腰直角三角形,符合AAS或ASA,或SAS,是全等形;
C、边长为3和4的两个等腰三角形有可能是3,3,4或4,4,3不一定全等对应关系不明确不一定全等;
D、一个钝角相等的两个等腰三角形.缺少对应边相等,不是全等形.
故选:B.
10.【解答】解:A、∵△ABC≌△DEF,∴AC=DF,故此结论正确;
B、∵△ABC≌△DEF,∴AB=DE;∵DB是公共边,∴AB﹣BD=DE﹣BD,即AD=BE;故此结论正确;
C、∵△ABC≌△DEF,∴AC=DF,故此结论DF=EF错误;
D、∵△ABC≌△DEF,∴BC=EF,故此结论正确;
故选:C.
二.填空题(共5小题)
11.【解答】解:设△ABC边BC上的高为h,
则△ABC的面积=BCh=×6h=9,
解得h=3,
∵△ABC≌△DEF,BC=EF,
∴EF边上的高是3cm.
故答案为:3.
12.【解答】解:如图所示:有3个点,当E在E、F、N处时,△ACE和△ACB全等,
点E的坐标是:(1,5),(1,﹣1),(5,﹣1),
故答案为:(1,5)或(1,﹣1)或(5,﹣1).
13.【解答】解:∵∠BAE=120°,∠BAD=40°,
∴∠DAE=∠BAE﹣∠BAD=120°﹣40°=80°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE=80°.
故答案为:80°.
14.【解答】解:∵△ABC≌△DEF,EF=5,
∴BC=EF=5,
∵△ABC的周长为12,AB=3,
∴AC=12﹣5﹣3=4.
故答案为:4.
15.【解答】解:由题意得:∠A′=70°,∠A=∠A′=70°,B′C′=BC=12,AD=A′D′=6.
故答案为:70°,70°,12,6.
三.解答题(共4小题)
16.【解答】方法一:
证明:∵△ABC≌△DEF,
∴AB=DE,∠B=∠E,
∵AM,DN分别是△ABC,△DEF的对应边上的高,
即AM⊥BC,DN⊥EF,
∴∠AMB=∠DNE=90°,
在△ABM和△DEN中,
∴△ABM≌△DEN(AAS),
∴AM=DN.
方法二:
∵△ABC≌△DEF,
∴BC=EF,
∵AM、DN分别是△ABC、△DEF的对应边上的高,
∴BCAM=EFDN,
∴AM=DN.
17.【解答】解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
18.【解答】解:∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°﹣40°﹣44°=96°.
19.【解答】解:(1)①当点P在BC上时,如图①﹣1,
若△APC的面积等于△ABC面积的一半;则CP=BC=cm,
此时,点P移动的距离为AC+CP=12+=,
移动的时间为:÷3=秒,
②当点P在BA上时,如图①﹣2
若△APC的面积等于△ABC面积的一半;则PD=BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+=cm,
移动的时间为:÷3=秒,
故答案为:或;
(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;
①当点P在AC上,如图②﹣1所示:
此时,AP=4,AQ=5,
∴点Q移动的速度为5÷(4÷3)=cm/s,
②当点P在AB上,如图②﹣2所示:
此时,AP=4,AQ=5,
即,点P移动的距离为9+12+15﹣4=32cm,点Q移动的距离为9+12+15﹣5=31cm,
∴点Q移动的速度为31÷(32÷3)=cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,
点Q的运动速为cm/s或cm/s
12.2三角形全等的判定
一.选择题
1.如图,在△ABC中,AB=AC,E、D分别为AB、AC边上的中点,连接BD、CE交于O,此图中全等三角形的对数为( )对.
A.4
B.3
C.2
D.1
2.如图,AB=AD,∠1=∠2,则不一定使△ABC≌△ADE的条件是( )
A.∠B=∠D
B.∠C=∠E
C.BC=DE
D.AC=AE
3.如图,A、B、C、D在一条直线上,MB=ND,∠MBA=∠D,添加下列某一条件后不能判定△ABM≌△CDN的是( )
A.∠M=∠N
B.AB=CD
C.AM=CN
D.AM∥CN
4.根据下列已知条件,能够画出唯一△ABC的是( )
A.AB=6,BC=5,∠A=50°
B.AB=5,BC=6,AC=13
C.∠A=50°,∠B=80°,AB=8
D.∠A=40°,∠B=50°,∠C=90°
5.如图,AD为∠BAC的平分线,添加下列条件后,不能证明△ABD≌△ACD的是( )
A.∠B=∠C
B.∠BDA=∠CDA
C.BD=CD
D.AB=AC
6.如图,给出的四组条件中,不能证明△ABC≌△DEF的是( )
A.AB=DE,BC=EF,AC=DF
B.AB=DE,∠B=∠E,BC=EF
C.AB=DE,AC=DF,∠B=∠E
D.∠B=∠E,BC=EF,∠C=∠F.
7.如图所示,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS
B.SAS
C.ASA
D.SSS
8.如图,要测量河两岸相对两点A、B间的距离,先在过点B的AB的垂线上取两点C、D,使得CD=BC,再在过点D的垂线上取点E,使A、C、E三点在一条直线上,可以证明△EDC≌△ABC,所以测得ED的长就是A、B两点间的距离,这里判定△EDC≌△ABC的理由是( )
A.SAS
B.SSS
C.ASA
D.AAS
9.如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
10.在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A',⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是( )
A.①②③
B.①②⑤
C.①②④
D.②⑤⑥
二.填空题
11.△ABC中,AB=5,AC=a,BC边上的中线AD=4,则a的取值范围是
.
12.如图,已知CA=DB,要使△ABC和△ABD全等,请补充条件
(填上一种即可).
13.如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=
.
14.已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:
①△ABD≌△EBC;
②∠BCE+∠BCD=180°;
③AF2=EC2﹣EF2;
④BA+BC=2BF.
其中正确的是
.
15.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则m+n
b+c.
三.解答题
16.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
17.已知:如图,E在△ABC的边AC上,且∠AEB=∠ABC.
(1)求证:∠ABE=∠C;
(2)若∠BAE的平分线AF交BE于点F,FD∥BC交AC于点D,设AB=8,AC=10,求DC的长.
18.如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=2,求△ABC的周长.
19.已知△ABC,点D、F分别为线段AC、AB上两点,连接BD、CF交于点E.
(1)若BD⊥AC,CF⊥AB,如图1所示,试说明∠BAC+∠BEC=180°;
(2)若BD平分∠ABC,CF平分∠ACB,如图2所示,试说明此时∠BAC与∠BEC的数量关系;
(3)在(2)的条件下,若∠BAC=60°,试说明:EF=ED.
参考答案与试题解析
一.选择题
1.【解答】解:∵AB=AC,
∴∠EBC=∠DCB,
∵AE=BE,AD=DC,
∴BE=DC,∵BC=CB,
∴△EBC≌△DCB,
∴∠ECB=∠DBC,
∴∠EBO=∠DCO,
∵BE=CD,∴∠BOE=∠COD,
∴△BOE≌△COD,
∵∠A=∠A,AB=AC,∠ABD=∠ACE,
∴△ABD≌△ACE,
共有3对全等三角形,
故选:B.
2.【解答】解:∵∠1=∠2,
∵∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
A、符合ASA定理,即能推出△ABC≌△ADE,故本选项错误;
B、符合AAS定理,即能推出△ABC≌△ADE,故本选项错误;
C、不符合全等三角形的判定定理,即不能推出△ABC≌△ADE,故本选项正确;
D、符合SAS定理,即能推出△ABC≌△ADE,故本选项错误;
故选:C.
3.【解答】解:A、根据ASA可以判定△ABM≌△CDN;
B、根据SAS可以判定△ABM≌△CDN;
C、SSA无法判定三角形全等;
D、根据AAS即可判定△ABM≌△CDN;
故选:C.
4.【解答】解:A、已知AB、BC和BC的对角,不能画出唯一三角形,故本选项错误;
B、∵AB+BC=5+6=11<AC,
∴不能画出△ABC;
故本选项错误;
C、已知两角和夹边,能画出唯一△ABC,故本选项正确;
D、根据∠A=40°,∠B=50°,∠C=90°不能画出唯一三角形,故本选项错误;
故选:C.
5.【解答】解:A、由,可得到△ABD≌△ACD,所以A选项不正确;
B、由,可得到△ABD≌△ACD,所以B选项不正确;
C、由BD=CD,AD=AD,∠BAD=∠CAD,不能得到△ABD≌△ACD,所以C选项正确.
D、由,可得到△ABD≌△ACD,所以D选项不正确;
故选:C.
6.【解答】解:A、由全等三角形的判定定理SSS能证明△ABC≌DEF,故此选项错误;
B、由全等三角形的判定定理SAS能证明△ABC≌DEF,故此选项错误;
C、由SSA不能证明△ABC≌DEF,故此选项正确;
D、由全等三角形的判定定理ASA能证明△ABC≌DEF,故此选项错误;
故选:C.
7.【解答】解:∵AC⊥BD,
∴∠ACB=∠ACD=90°,
在△ACB和△ACD中,
,
∴△ACB≌△ACD(SAS),
∴AB=AD(全等三角形的对应边相等).
故选:B.
8.【解答】解:∵AB⊥BD,ED⊥BD,
∴∠ABD=∠EDC=90°,
在△EDC和△ABC中,
,
∴△EDC≌△ABC(ASA)
故选:C.
9.【解答】解:第一块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;
第二块,仅保留了原三角形的一部分边,所以该块不行;
第三块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去.
故选:C.
10.【解答】解:∵在△ABC和△A′B′C′中,有边边角、角角角不能判定三角形全等,
∴①②④是边边角,
∴不能保证△ABC≌△A′B′C′.
故选:C.
二.填空题(共5小题)
11.【解答】解:延长AD到E,使AD=DE,连接BE,
∵AD=DE,∠ADC=∠BDE,BD=DC,
∴△ADC≌△EDB(SAS)
∴BE=AC=a,
在△AEB中,AB﹣BE<AE<AB+BE,
即5﹣a<2AD<5+a,
∴<AD<.,
∵AD=4,
∴a的取值范围是3<a<13,
故答案为:3<a<13
12.【解答】解:当CB=DA时,△ABC≌△ABD,
在△ABC和△ABD中,
,
∴△ABC≌△ABD(SSS),
故答案为:CB=DA.
13.【解答】解:∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴AC=DF=5(全等三角形对应边相等).
故答案为:5.
14.【解答】解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS),
∴①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,
∴②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC,
∵EF⊥AB,
∴AF2=EC2﹣EF2;
∴③正确;
④如图,过E作EG⊥BC于G点,
∵E是BD上的点,∴EF=EG,
在Rt△BEG和Rt△BEF中,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
在Rt△CEG和Rt△AFE中,
,
∴Rt△CEG≌Rt△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF,
∴④正确.
故答案为:①②③④.
15.【解答】解:如图,在BA的延长线上取点E,使AE=AC,连接EP,
∵AD是∠A的外角平分线,
∴∠CAD=∠EAD,
在△ACP和△AEP中,
,
∴△ACP≌△AEP(SAS),
∴PE=PC,
在△PBE中,PB+PE>AB+AE,
∵PB=m,PC=n,AB=c,AC=b,
∴m+n>b+c.
故答案为:>.
三.解答题(共4小题)
16.【解答】(1)证明:∵AB∥CD,
∴∠B=∠C,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(AAS),
∴AB=CD;
(2)解:∵△ABE≌△DCF,
∴AB=CD,BE=CF,∠B=∠C,
∵∠B=40°,
∴∠C=40°
∵AB=CF,
∴CF=CD,
∴∠D=∠CFD=(180°﹣40°)=70°.
17.【解答】(1)证明:在△ABE中,∠ABE=180°﹣∠BAE﹣∠AEB,
在△ABC中,∠C=180°﹣∠BAC﹣∠ABC,
∵∠AEB=∠ABC,∠BAE=∠BAC,
∴∠ABE=∠C;
(2)解:∵FD∥BC,
∴∠ADF=∠C,
又∠ABE=∠C,
∴∠ABE=∠ADF,
∵AF平分∠BAE,
∴∠BAF=∠DAF,
在△ABF和△ADF中,
,
∴△ABF≌△ADF(AAS),
∴AB=AD,
∵AB=8,AC=10,
∴DC=AC﹣AD=AC﹣AB=10﹣8=2.
18.【解答】(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵AB=AC,
∴∠B=∠C(等边对等角).
∵D是BC的中点,
∴BD=CD.
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS).
∴DE=DF
(2)解:∵AB=AC,∠A=60°,
∴△ABC为等边三角形.
∴∠B=60°,
∵∠BED=90°,
∴∠BDE=30°,
∴BE=BD,
∵BE=2,
∴BD=4,
∴BC=2BD=8,
∴△ABC的周长为24.
19.【解答】解:(1)∵BD⊥AC,CF⊥AB,
∴∠DCE+∠DEC=∠DCE+∠FAC=90°,
∴∠DEC=∠BAC,∠DEC+∠BEC=180°,
∴∠BAC+∠BEC=180°;
(2)∵BD平分∠ABC,CF平分∠ACB,
∴∠EBC=ABC,∠ECB=ACB,∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠BAC)=90°∠BAC;
(3)作∠BEC的平分线EM交BC于M,
∵∠BAC=60°,
∴∠BEC=90°+BAC=120°,
∴∠FEB=∠DEC=60°,
∵EM平分∠BEC,
∴∠BEM=60°,
在△FBE与△EBM中,
12.3《角平分线性质》
、选择题
如图,在△ACB中,∠ACB=100°,∠A=20°,D是AB上一点.将△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于(
)
A.25°
B.30°
C.35°
D.40°
如图,已知∠AOB.
按照以下步骤作图:
①以点O为圆心,以适当的长为半径作弧,分别交∠AOB的两边于C,D两点,连接CD.
②分别以点C,D为圆心,以大于线段OC的长为半径作弧,两弧在∠AOB内交于点E,
连接CE,DE.
③连接OE交CD于点M.
下列结论中错误的是( )
A.∠CEO=∠DEO
B.CM=MD
C.∠OCD=∠ECD
D.S四边形OCED=CD?OE
如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于(
)
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,若BC=7,则AE的长为( )
A.4
B.5
C.6
D.7
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有(
)
A.4个
B.3个
C.2个
D.1个
如图,已知∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=3,则BE=(
)
A.
6
B.
3
C.
2
D.
1.5
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长是(
)
A.6cm
B.4cm
C.10cm
D.以上都不对
如图,已知OQ平分∠AOB,点P为OQ上任意一点,点N为OA上一点,点M为OB上一点,若∠PNO+∠PMO=180°,则PM和PN的大小关系是(
)
A.PM>PN
B.PM<PN
C.PM=PN
D.不能确定
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为(
)
A.25°
B.30°
C.35°
D.40°
如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是(
)
A.56°
B.60°
C.68°
D.94°
如图所示,在Rt△ABC中,AD是斜边上的高,∠ABC的平分线分别交AD、AC于点F、E,EG⊥BC于G,下列结论正确的是(
)
A.∠C=∠ABC
B.BA=BG
C.AE=CE
D.AF=FD
如图,BD为∠ABC的角平分线,且BD=BC,E为BD的延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.
下列结论:
①∠ABE=∠ACE;②∠BCE+∠BCD=180°;③AE=EC;④BE+BD=2BF,其中正确的是( )
A.①②③
B.①③④
C.①②④
D.①②③④
、填空题
如图,在△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB,AC=8cm,AE=4cm,则DE的长是 .
如图,AD是△ABC的角平分线,DE⊥AB于E,若AB=18,AC=12,△ABC的面积等于36,则DE= .
若△ABC的周长为41
cm,边BC=17
cm,AB
.如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,∠BOC=
.
如图所示,已知△ABC的周长是18,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的面积是 .
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为?
???.
、解答题
如图所示,已知AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F.
求证:DE=DF.
如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
如图,△ABC中,AD是∠CAB的平分线,且AB=AC+CD,求证:∠C=2∠B.
如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC.
求证:∠A+∠C=180°.
(1)如图1,△ABC中,作∠ABC、∠ACB的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
①
求证:OE=BE;
②
若△ABC
的周长是25,BC=9,试求出△AEF的周长;
(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,试探求∠BAC
与∠PAC的数量关系式.
参考答案
D
答案为:C.
C
D
答案为:A;
答案为:D;
A.
C
C
A
B
答案为:D.
答案为:3cm.
答案为:2.4.
答案为:9;
答案为:125°.
答案为:36.
答案为:6;
证明:连接AD,
在△ACD和△ABD中,,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
证明:(1)过O点作OE⊥AC于点E.
∵∠ABD=90°且OA平分∠BAC
∴OB=OE,
又∵O是BD中点
∴OB=OD,
∴OE=OD,
∵OE⊥AC,∠D=90°
∴点O在∠ACD
的角平分线上
∴OC平分∠ACD.
(2)在Rt△ABO和Rt△AEO中
∵
∴Rt△ABO≌Rt△AEO(HL),
∴AB=AE,
在Rt△CDO和Rt△CEO中
∵
∴Rt△CDO≌Rt△CEO(HL),
∴CD=CE,
∴AB+CD=AE+CE=AC.
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
证明:延长AC至E,使CE=CD,连接ED
∵AB=AC+CD
∴AE=AB
∵AD平分∠CAB
∴∠EAD=∠BAD
∴AE=AB,∠EAD=∠BAD,AD=AD
∴△ADE≌△ADB
∴∠E=∠B且∠ACD=∠E+∠CDE,CE=CD
∴∠ACD=∠E+∠CDE=2∠E=2∠B
即∠C=2∠B
证明:过点D作DE⊥BC于E,过点D作DF⊥AB交BA的延长线于F,
∵BD平分∠ABC,
∴DE=DF,∠DEC=∠F=90°,
在RtCDE和Rt△ADF中,
,
∴Rt△CDE≌Rt△ADF(HL),
∴∠FAD=∠C,
∴∠BAD+∠C=∠BAD+∠FAD=180°.
(1)∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EDB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE
(2)△AEF的周长=AE+AF+EF=AE+AF+EB+FC=AB+AC=25-9=16
(3)延长BA,证明P点在∠BAC外角的角平分线上,
从而得到2∠PAC+∠BAC=180°
