苏科版八年级上册 第六章 一次函数应用(图像综合)解答题题拔高训练(三)(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册 第六章 一次函数应用(图像综合)解答题题拔高训练(三)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 80.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 10:42:05 | ||
图片预览




文档简介
第六章
一次函数应用(图像综合)
解答题题拔高训练(三)
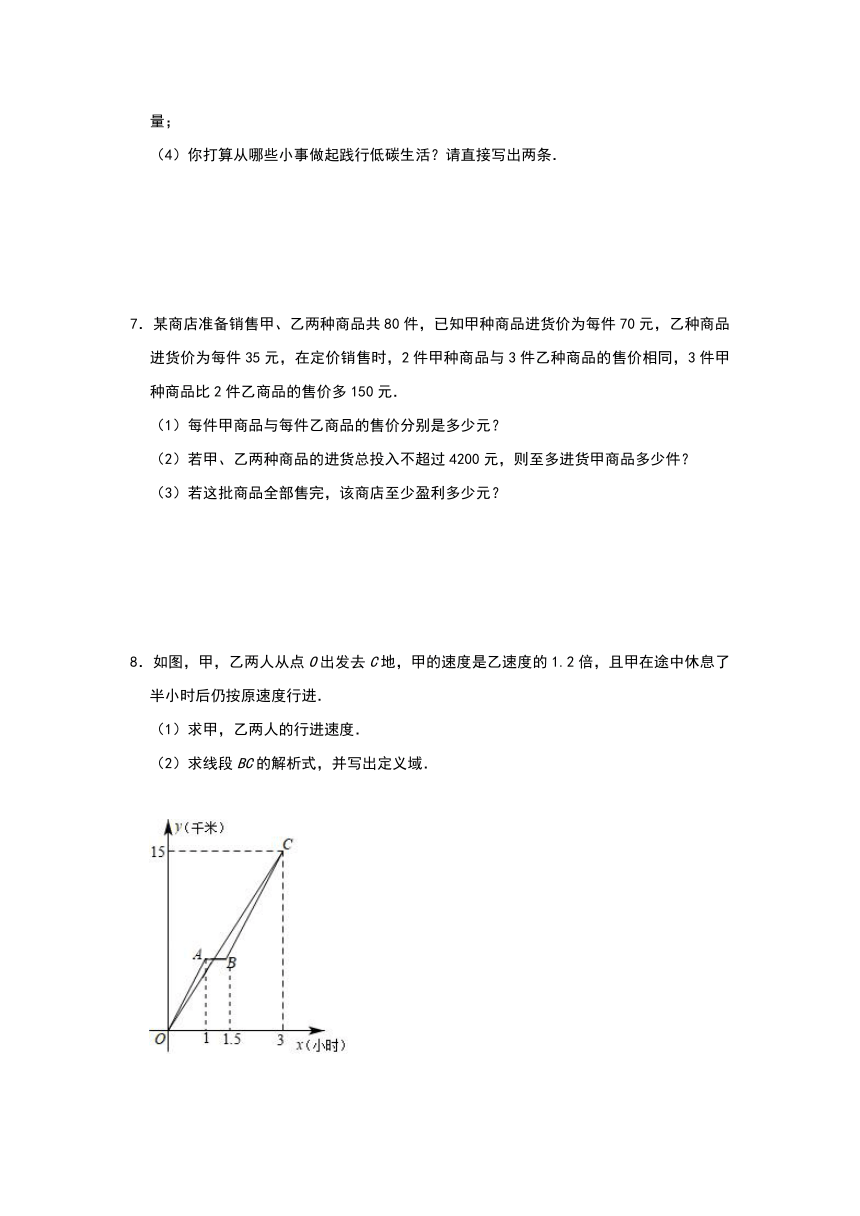
1.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,根据图象所提供的信息分析,解决下列问题:
(1)甲队的工作速度;
(2)分别求出乙队在0≤x≤2和2≤x≤6时段,y与x的函数解析式,并求出甲乙两队所挖河渠长度相等时x的值;
(3)当两队所挖的河渠长度之差为5m时x的值.
2.某城市居民用水实行阶梯收费,每户每月用水量如果未超过15吨,按每吨2元收费.如果超过15吨,未超过的部分仍按每吨2元收费,超过部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出当每月用水量未超过15吨和超过15吨时,y与x之间的函数表达式;
(2)当某月用水量为20吨,求该月应交的水费;
(3)若该城市某用户5月份和6月份共用水50吨,且5月份的用水量不足15吨,两个月一共交水费120元,求该用户5月份和6月份分别用水多少吨?
3.某学校计划在总费用为3200元的限额内,租用汽车送312名学生和8名教师集体外出活动,每辆汽车上至少要有1名教师;现有甲乙两种大客车,它们的载客量和租金如下表:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
(1)通过计算与分析后,直接写出共需租用
辆汽车;
(2)求出有哪几种租车方案;
(3)求出最节省的租车费用是多少元.
4.小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需
小时,此时离家
千米.
(2)求小明出发两个半小时离家多远?(写出解答过程)
(3)求小明出发多长时间离家12千米?
5.2020年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至5月,中国已经向150多个国家和国际组织提供医疗物质援助.某次援助,我国组织20架飞机装运口罩、消毒剂、防护服三种医疗物质共120吨,按计划20架飞机都要装运,每架飞机只能装运同一种医疗物质,且必须装满.根据如表提供的信息,解答以下问题:
防疫物质种类
口罩
消毒剂
防护服
每架飞机运载量(吨)
8
5
4
每吨物资运费(元)
1200
1600
1000
(1)若有9架飞机装运口罩,有a架飞机装运消毒剂,求a的值;
(2)若有x架飞机装运口罩,有y架飞机装运消毒剂,求y与x之间的函数关系式;
(3)如果装运每种医疗物质的飞机都不少于4架,那么飞机的安排方案有几种?这些方案中,若要使此次物质运费最小,应采取哪个方案?
6.你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.排碳计算公式:
家居用电的二氧化碳排放量(kg)=耗电量(kW?h)×0.785
开私家车的二氧化碳排放量(kg)=耗油量(L)×2.7
家用天然气二氧化碳排放量(kg)=天然气使用量(m3)×0.19
家用自来水二氧化碳排放量(kg)=自来水使用量(t)×0.91
(1)如果用x(L)表示耗油量,用y(kg)表示开私家车的二氧化碳排放量,则y与x之间的关系式可表示为
;
(2)在上述关系式中,耗油量每增加1L,二氧化碳排放量增加
kg.当耗油量从10L增加到100L时,二氧化碳排放量从
kg增加到
kg;
(3)小颖家本月家居用电的耗电量约为90kW?h,开私家车的耗油量约为70L,天然气使用量约20m3,自来水使用量约6吨,请你计算一下小颖家本月这几项的二氧化碳排放总量;
(4)你打算从哪些小事做起践行低碳生活?请直接写出两条.
7.某商店准备销售甲、乙两种商品共80件,已知甲种商品进货价为每件70元,乙种商品进货价为每件35元,在定价销售时,2件甲种商品与3件乙种商品的售价相同,3件甲种商品比2件乙商品的售价多150元.
(1)每件甲商品与每件乙商品的售价分别是多少元?
(2)若甲、乙两种商品的进货总投入不超过4200元,则至多进货甲商品多少件?
(3)若这批商品全部售完,该商店至少盈利多少元?
8.如图,甲,乙两人从点O出发去C地,甲的速度是乙速度的1.2倍,且甲在途中休息了半小时后仍按原速度行进.
(1)求甲,乙两人的行进速度.
(2)求线段BC的解析式,并写出定义域.
9.如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O﹣D﹣E﹣F表示y1与x的函数图象;折线O﹣G﹣F表示y2与x的函数图象.
(1小明的速度为
m/min,图②中a的值为
.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
10.小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,16min时到家,假设小东始终以100m/min的速度步行,两人离家的距离y(单位:m)与小东打完电话后的步行时间t(单位;min)之间的函数关系如图所示:
(1)小东打电话时,他离家
m;
(2)填上图中空格相应的数据
,
,
;
(3)小东和妈妈相遇后,妈妈回家的速度为
m/min;
(4)
min时,两人相距700m.
参考答案
1.解:(1)甲队的工作速度为:60÷6=10(米/小时);
(2)当0≤x≤2时,设y与x的函数解析式为y=kx,可得2k=30,解得k=15,即y=15x;
当2≤x≤6时,设y与x的函数解析式为y=nx+m,可得,解得,即y=5x+20,
∴;
10x=5x+20,解得x=4,
即甲乙两队所挖河渠长度相等时x的值为4;
(3)当0≤x≤2时,15x﹣10x=5,解得x=1.
当2<x≤4时,5x+20﹣10x=5,解得x=3,
当4<x≤6时,10x﹣(5x+20)=5,解得x=5.
答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.
2.解:(1)由题意可得,
当0≤x≤15时,y=2x,
当x>15时,y=15×2+(x﹣15)×2.8=2.8x﹣12,
即当0≤x≤15时,y=2x,当x>15时,y=2.8x﹣12;
(2)当x=20时,
y=2.8×20﹣12=44,
即当某月用水量为20吨,该月应交的水费为44元;
(3)设5月份用水x吨,
由题意可得,2x+[2.8(50﹣x)﹣12]=120,
解得x=10,
∴50﹣x=40,
答:该用户5月份和6月份分别用水10吨、40吨.
3.解:(1)如果全部租用甲种客车,则需要(312+8)÷45=7(辆),
如果全部租用乙种客车,则需要(312+8)÷30=10(辆),
∵汽车辆数为整数,且有8名教师,每辆汽车上至少要有1名教师,
∴共租用8辆汽车,
故答案为:8;
(2)设租用x辆甲种客车,则租用乙种客车(8﹣x)辆,
则租车费用y=400x+280(8﹣x)=120x+2240,
∵,
解得,5≤x≤8,
∵x为整数,
∴x=6或7或8,
∴共有3种租车方案,
方案一:6辆甲种客车,2辆乙种客车;
方案二:7辆甲种客车,1辆乙种客车;
方案三:8辆甲种客车;
(3)∵y=120x+2240中,k=120>0,
∴y随x的增大而增大,
∴当x=6时,y有最小值,最节省的租车费用是2960元,
答:最节省的租车费用是2960元.
4.解:(1)由图象可得,
小明到达离家最远的地方需3小时,此时离家25千米,
故答案为:3,25;
(2)当2≤x≤3时,设y与x的函数关系式为y=kx+b,
,得,
即当2≤x≤3时,y与x的函数关系式为y=10x﹣5,
当x=2.5时,y=10×2.5﹣5=20,
即小明出发两个半小时离家20千米;
(3)当0≤x≤1时,设y与x的函数关系式为y=ax,
a=15,
即当0≤x≤1时,y与x的函数关系式为y=15x,
当y=12时,12=15x,得x=,
当4≤x≤6时,设y与x的函数关系式为y=mx+n,
,得,
即当4≤x≤6时,y与x的函数关系式为y=﹣12.5x+75,
当y=12时,12=﹣12.5x+75,得x=,
答:小明出发小时或小时时离家12千米.
5.解:(1)根据题意得:8×9+5a+4(20﹣9﹣a)=120,
解得:a=4,
答:a的值为4;
(2)根据题意得:8x+5y+4(20﹣x﹣y)=120,
化简得y=﹣4x+40,
所以,y与x之间的函数关系式为y=﹣4x+40;
(3)根据题意得:
,
∴8≤x≤9,
∵x为整数,
∴x=8或9,
设此次物资运费为W元,
∴W=﹣2200x+44000,
∵k=﹣2200<0,
∴W随x的增大而减小,
∴x=9,W最小.
答:飞机安排的方案有2种,选择运口罩9架,运消毒剂4架,运防护服7架,运费最小.
6.解:(1)由题意可得y=2.7x;
(2)由y=2.7x可知,耗油量每增加1L,二氧化碳排放量增加2.7kg.当耗油量从10L增加到100L时,二氧化碳排放量从27kg增加到270kg;
(3)90×0.785+70×2.7+20×0.19+6×0.91=268.91(kg),
小颖家本月这几项的二氧化碳排放总量为268.91kg.
(4)我们可以从小事做起践行低碳生活,如节约用水用电;外出乘坐公交等.
故答案为:(1)y=2.7x;(2)2.7,27,270.
7.解:(1)设每件甲商品与每件乙商品的售价分别是x、y元.
依题意得:,
解得;
(2)设进货甲商品a件,则乙商品(80﹣a)件.
依题意得:70a+35(80﹣a)≤4200
解得a≤40;
(3)设进货乙商品b件,利润为M元.
由(2)得a≤40,则b≥40
M=(90﹣70)(80﹣b)+(60﹣35)b=5b+1600
∵5>0
∴M随b的增大而增大
∴当b=40时,M取得最小值,即5×40+1600=1800(元)
8.解:(1)由图知,乙的速度=15÷3=5千米/小时,
∵甲的速度是乙速度的1.2倍,
∴5×1.2=6千米/小时,
即甲,乙两人的行进速度分别是6千米/小时、5千米/小时;
(2)∵点A的纵坐标为6×1=6,
∴点B的坐标为(1.5,6),
设线段BC的解析式为y=kx+b,
,得,
即线段BC的解析式是y=6x﹣3(1.5≤x≤3).
9.解:(1)小明的速度为=60(m/min);妈妈的速度==200(m/min),
=9(min),
24+9=33(min),
∴a=33min,
故答案为:60,33min.
(2)小明妈妈的速度为200
m/min,
∵当12≤x≤30,小明与妈妈同向而行,小明的速度为60
m/min,
∴当x=12时,两人之间的距离为:2400+60×12=3210(m),
∴y=3120﹣(200﹣60)(x﹣12),
即y=﹣140
x+4800.
10.解:(1)由图象可得,
小东打电话时,他离家1400m,
故答案为:1400;
(2)由图可得,
小东行驶6min对应的y的值为:1400﹣6×100=800,
小东行驶到22min时对应的y值为:(1400﹣6×100)+(22﹣6)×100=2400,
小东行驶到27min时对应的y值为:(1400﹣6×100)+(27﹣6)×100=2900,
故答案为:800,2400,2900;
(3)小东和妈妈相遇后,妈妈回家的速度为:=50(m/min),
故答案为:50;
(4)设在tmin时,两人相距700m,
相遇前相距700m,t==3,
相遇后相距700m,t=6+=,
故答案为:3或.
一次函数应用(图像综合)
解答题题拔高训练(三)
1.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示,根据图象所提供的信息分析,解决下列问题:
(1)甲队的工作速度;
(2)分别求出乙队在0≤x≤2和2≤x≤6时段,y与x的函数解析式,并求出甲乙两队所挖河渠长度相等时x的值;
(3)当两队所挖的河渠长度之差为5m时x的值.
2.某城市居民用水实行阶梯收费,每户每月用水量如果未超过15吨,按每吨2元收费.如果超过15吨,未超过的部分仍按每吨2元收费,超过部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)分别写出当每月用水量未超过15吨和超过15吨时,y与x之间的函数表达式;
(2)当某月用水量为20吨,求该月应交的水费;
(3)若该城市某用户5月份和6月份共用水50吨,且5月份的用水量不足15吨,两个月一共交水费120元,求该用户5月份和6月份分别用水多少吨?
3.某学校计划在总费用为3200元的限额内,租用汽车送312名学生和8名教师集体外出活动,每辆汽车上至少要有1名教师;现有甲乙两种大客车,它们的载客量和租金如下表:
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金(单位:元/辆)
400
280
(1)通过计算与分析后,直接写出共需租用
辆汽车;
(2)求出有哪几种租车方案;
(3)求出最节省的租车费用是多少元.
4.小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
(1)根据图象回答:小明到达离家最远的地方需
小时,此时离家
千米.
(2)求小明出发两个半小时离家多远?(写出解答过程)
(3)求小明出发多长时间离家12千米?
5.2020年新冠肺炎疫情在全球蔓延,全球疫情大考面前,中国始终同各国安危与共、风雨同舟,时至5月,中国已经向150多个国家和国际组织提供医疗物质援助.某次援助,我国组织20架飞机装运口罩、消毒剂、防护服三种医疗物质共120吨,按计划20架飞机都要装运,每架飞机只能装运同一种医疗物质,且必须装满.根据如表提供的信息,解答以下问题:
防疫物质种类
口罩
消毒剂
防护服
每架飞机运载量(吨)
8
5
4
每吨物资运费(元)
1200
1600
1000
(1)若有9架飞机装运口罩,有a架飞机装运消毒剂,求a的值;
(2)若有x架飞机装运口罩,有y架飞机装运消毒剂,求y与x之间的函数关系式;
(3)如果装运每种医疗物质的飞机都不少于4架,那么飞机的安排方案有几种?这些方案中,若要使此次物质运费最小,应采取哪个方案?
6.你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳(特别是二氧化碳)的排放量的一种生活方式.排碳计算公式:
家居用电的二氧化碳排放量(kg)=耗电量(kW?h)×0.785
开私家车的二氧化碳排放量(kg)=耗油量(L)×2.7
家用天然气二氧化碳排放量(kg)=天然气使用量(m3)×0.19
家用自来水二氧化碳排放量(kg)=自来水使用量(t)×0.91
(1)如果用x(L)表示耗油量,用y(kg)表示开私家车的二氧化碳排放量,则y与x之间的关系式可表示为
;
(2)在上述关系式中,耗油量每增加1L,二氧化碳排放量增加
kg.当耗油量从10L增加到100L时,二氧化碳排放量从
kg增加到
kg;
(3)小颖家本月家居用电的耗电量约为90kW?h,开私家车的耗油量约为70L,天然气使用量约20m3,自来水使用量约6吨,请你计算一下小颖家本月这几项的二氧化碳排放总量;
(4)你打算从哪些小事做起践行低碳生活?请直接写出两条.
7.某商店准备销售甲、乙两种商品共80件,已知甲种商品进货价为每件70元,乙种商品进货价为每件35元,在定价销售时,2件甲种商品与3件乙种商品的售价相同,3件甲种商品比2件乙商品的售价多150元.
(1)每件甲商品与每件乙商品的售价分别是多少元?
(2)若甲、乙两种商品的进货总投入不超过4200元,则至多进货甲商品多少件?
(3)若这批商品全部售完,该商店至少盈利多少元?
8.如图,甲,乙两人从点O出发去C地,甲的速度是乙速度的1.2倍,且甲在途中休息了半小时后仍按原速度行进.
(1)求甲,乙两人的行进速度.
(2)求线段BC的解析式,并写出定义域.
9.如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O﹣D﹣E﹣F表示y1与x的函数图象;折线O﹣G﹣F表示y2与x的函数图象.
(1小明的速度为
m/min,图②中a的值为
.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.当12≤x≤30时,求出y与x的函数表达式.
10.小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回,16min时到家,假设小东始终以100m/min的速度步行,两人离家的距离y(单位:m)与小东打完电话后的步行时间t(单位;min)之间的函数关系如图所示:
(1)小东打电话时,他离家
m;
(2)填上图中空格相应的数据
,
,
;
(3)小东和妈妈相遇后,妈妈回家的速度为
m/min;
(4)
min时,两人相距700m.
参考答案
1.解:(1)甲队的工作速度为:60÷6=10(米/小时);
(2)当0≤x≤2时,设y与x的函数解析式为y=kx,可得2k=30,解得k=15,即y=15x;
当2≤x≤6时,设y与x的函数解析式为y=nx+m,可得,解得,即y=5x+20,
∴;
10x=5x+20,解得x=4,
即甲乙两队所挖河渠长度相等时x的值为4;
(3)当0≤x≤2时,15x﹣10x=5,解得x=1.
当2<x≤4时,5x+20﹣10x=5,解得x=3,
当4<x≤6时,10x﹣(5x+20)=5,解得x=5.
答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.
2.解:(1)由题意可得,
当0≤x≤15时,y=2x,
当x>15时,y=15×2+(x﹣15)×2.8=2.8x﹣12,
即当0≤x≤15时,y=2x,当x>15时,y=2.8x﹣12;
(2)当x=20时,
y=2.8×20﹣12=44,
即当某月用水量为20吨,该月应交的水费为44元;
(3)设5月份用水x吨,
由题意可得,2x+[2.8(50﹣x)﹣12]=120,
解得x=10,
∴50﹣x=40,
答:该用户5月份和6月份分别用水10吨、40吨.
3.解:(1)如果全部租用甲种客车,则需要(312+8)÷45=7(辆),
如果全部租用乙种客车,则需要(312+8)÷30=10(辆),
∵汽车辆数为整数,且有8名教师,每辆汽车上至少要有1名教师,
∴共租用8辆汽车,
故答案为:8;
(2)设租用x辆甲种客车,则租用乙种客车(8﹣x)辆,
则租车费用y=400x+280(8﹣x)=120x+2240,
∵,
解得,5≤x≤8,
∵x为整数,
∴x=6或7或8,
∴共有3种租车方案,
方案一:6辆甲种客车,2辆乙种客车;
方案二:7辆甲种客车,1辆乙种客车;
方案三:8辆甲种客车;
(3)∵y=120x+2240中,k=120>0,
∴y随x的增大而增大,
∴当x=6时,y有最小值,最节省的租车费用是2960元,
答:最节省的租车费用是2960元.
4.解:(1)由图象可得,
小明到达离家最远的地方需3小时,此时离家25千米,
故答案为:3,25;
(2)当2≤x≤3时,设y与x的函数关系式为y=kx+b,
,得,
即当2≤x≤3时,y与x的函数关系式为y=10x﹣5,
当x=2.5时,y=10×2.5﹣5=20,
即小明出发两个半小时离家20千米;
(3)当0≤x≤1时,设y与x的函数关系式为y=ax,
a=15,
即当0≤x≤1时,y与x的函数关系式为y=15x,
当y=12时,12=15x,得x=,
当4≤x≤6时,设y与x的函数关系式为y=mx+n,
,得,
即当4≤x≤6时,y与x的函数关系式为y=﹣12.5x+75,
当y=12时,12=﹣12.5x+75,得x=,
答:小明出发小时或小时时离家12千米.
5.解:(1)根据题意得:8×9+5a+4(20﹣9﹣a)=120,
解得:a=4,
答:a的值为4;
(2)根据题意得:8x+5y+4(20﹣x﹣y)=120,
化简得y=﹣4x+40,
所以,y与x之间的函数关系式为y=﹣4x+40;
(3)根据题意得:
,
∴8≤x≤9,
∵x为整数,
∴x=8或9,
设此次物资运费为W元,
∴W=﹣2200x+44000,
∵k=﹣2200<0,
∴W随x的增大而减小,
∴x=9,W最小.
答:飞机安排的方案有2种,选择运口罩9架,运消毒剂4架,运防护服7架,运费最小.
6.解:(1)由题意可得y=2.7x;
(2)由y=2.7x可知,耗油量每增加1L,二氧化碳排放量增加2.7kg.当耗油量从10L增加到100L时,二氧化碳排放量从27kg增加到270kg;
(3)90×0.785+70×2.7+20×0.19+6×0.91=268.91(kg),
小颖家本月这几项的二氧化碳排放总量为268.91kg.
(4)我们可以从小事做起践行低碳生活,如节约用水用电;外出乘坐公交等.
故答案为:(1)y=2.7x;(2)2.7,27,270.
7.解:(1)设每件甲商品与每件乙商品的售价分别是x、y元.
依题意得:,
解得;
(2)设进货甲商品a件,则乙商品(80﹣a)件.
依题意得:70a+35(80﹣a)≤4200
解得a≤40;
(3)设进货乙商品b件,利润为M元.
由(2)得a≤40,则b≥40
M=(90﹣70)(80﹣b)+(60﹣35)b=5b+1600
∵5>0
∴M随b的增大而增大
∴当b=40时,M取得最小值,即5×40+1600=1800(元)
8.解:(1)由图知,乙的速度=15÷3=5千米/小时,
∵甲的速度是乙速度的1.2倍,
∴5×1.2=6千米/小时,
即甲,乙两人的行进速度分别是6千米/小时、5千米/小时;
(2)∵点A的纵坐标为6×1=6,
∴点B的坐标为(1.5,6),
设线段BC的解析式为y=kx+b,
,得,
即线段BC的解析式是y=6x﹣3(1.5≤x≤3).
9.解:(1)小明的速度为=60(m/min);妈妈的速度==200(m/min),
=9(min),
24+9=33(min),
∴a=33min,
故答案为:60,33min.
(2)小明妈妈的速度为200
m/min,
∵当12≤x≤30,小明与妈妈同向而行,小明的速度为60
m/min,
∴当x=12时,两人之间的距离为:2400+60×12=3210(m),
∴y=3120﹣(200﹣60)(x﹣12),
即y=﹣140
x+4800.
10.解:(1)由图象可得,
小东打电话时,他离家1400m,
故答案为:1400;
(2)由图可得,
小东行驶6min对应的y的值为:1400﹣6×100=800,
小东行驶到22min时对应的y值为:(1400﹣6×100)+(22﹣6)×100=2400,
小东行驶到27min时对应的y值为:(1400﹣6×100)+(27﹣6)×100=2900,
故答案为:800,2400,2900;
(3)小东和妈妈相遇后,妈妈回家的速度为:=50(m/min),
故答案为:50;
(4)设在tmin时,两人相距700m,
相遇前相距700m,t==3,
相遇后相距700m,t=6+=,
故答案为:3或.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
