河北省石家庄市赵县2020-2021学年第一学期八年级上数学期中考试试卷 (Word版 含解析)
文档属性
| 名称 | 河北省石家庄市赵县2020-2021学年第一学期八年级上数学期中考试试卷 (Word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览


文档简介
河北省石家庄市赵县2020-2021学年八年级上学期数学期中试卷
一、选择题(本大题有16个小题,共42分。其中1- 10小题各3分,11-16小题各2分)
1.下列各图形中,具有稳定性的是( )
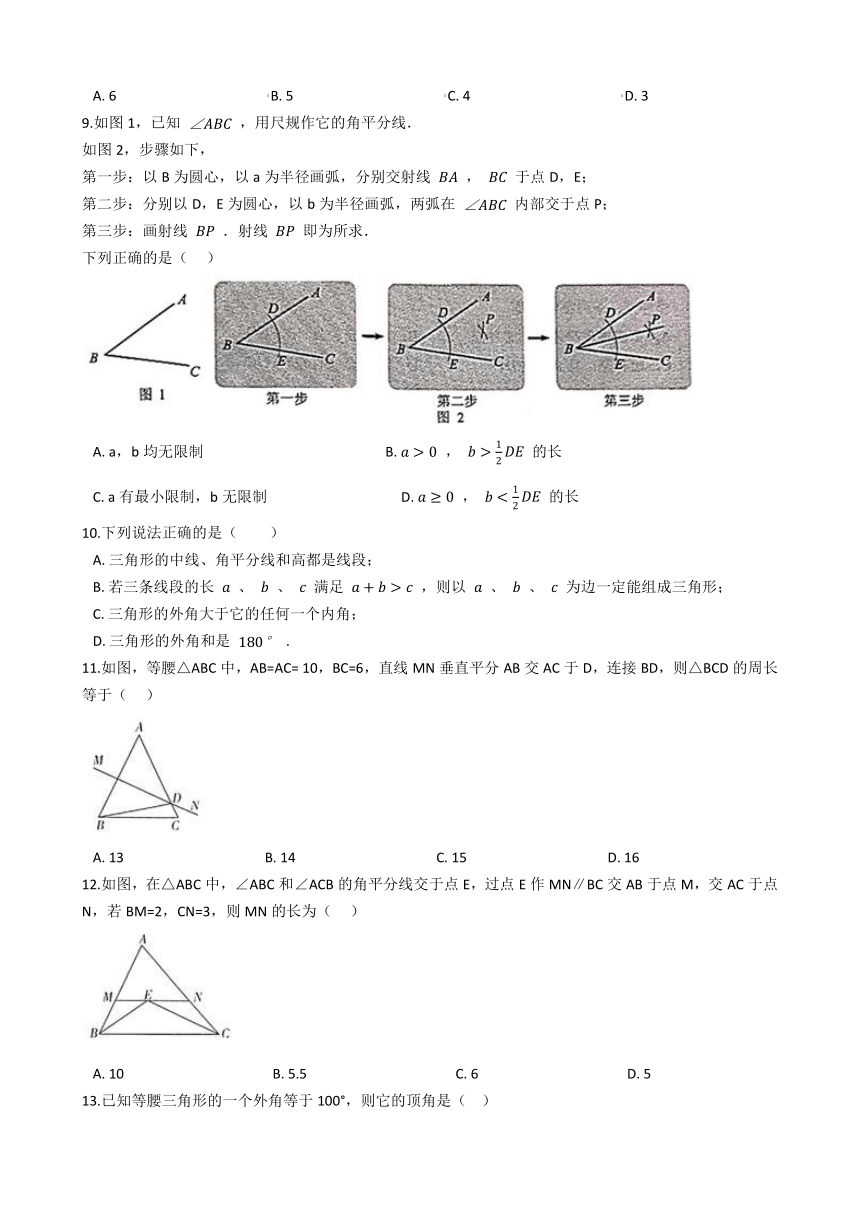
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.现实世界中,对称现象无处不在,中国的方块字中有的也具有对称性,下列汉字是轴对称图形的是( ???)
A.?爱?????????????????????????????????????????B.?我?????????????????????????????????????????C.?中?????????????????????????????????????????D.?华
3.小晶有两根长度为5cm、8cm的木条,她想钉一个三角形的木框,现在有长度分别为2cm、3cm、8cm、15cm的木条供她选择,那她第三根应选择( ???)
A.?2cm????????????????????????????????????B.?3cm????????????????????????????????????C.?8cm????????????????????????????????????D.?15cm
4.如果三角形的一个外角与它不相邻的两个内角的和为 180° ,那么这个三角形是(??? )
A.?直角三角形????????????????????????B.?钝角三角形????????????????????????C.?锐角三角形????????????????????????D.?无法确定
5.图中能表示 △ABC 的BC边上的高的是 ( ??? )
A.???????????????????B.???????????????????C.???????????????????D.?
6.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( ???)
A.?角平分线????????????????????????????????B.?中线????????????????????????????????C.?高????????????????????????????????D.?任意一条线
7.如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为( ???)
A.?55°???????????????????????????????????????B.?35°???????????????????????????????????????C.?45°???????????????????????????????????????D.?25°
8.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,点P到边OB的距离为4,则PD=(?? )
A.?6???????????????????????????????????????????B.?5???????????????????????????????????????????C.?4???????????????????????????????????????????D.?3
9.如图1,已知 ∠ABC ,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线 BA , BC 于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在 ∠ABC 内部交于点P;
第三步:画射线 BP .射线 BP 即为所求.
下列正确的是(??? )
A.?a,b均无限制?????????????????????????????????????????????????????B.?a>0 , b>12DE 的长
C.?a有最小限制,b无限制???????????????????????????????????????D.?a≥0 , b<12DE 的长
10.下列说法正确的是(??????? )
A.?三角形的中线、角平分线和高都是线段;
B.?若三条线段的长 a 、 b 、 c 满足 a+b>c ,则以 a 、 b 、 c 为边一定能组成三角形;
C.?三角形的外角大于它的任何一个内角;
D.?三角形的外角和是 180° .
11.如图,等腰△ABC中,AB=AC= 10,BC=6,直线MN垂直平分AB交AC于D,连接BD,则△BCD的周长等于( ???)
A.?13?????????????????????????????????????????B.?14?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
12.如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM=2,CN=3,则MN的长为( ???)
A.?10??????????????????????????????????????????B.?5.5??????????????????????????????????????????C.?6??????????????????????????????????????????D.?5
13.已知等腰三角形的一个外角等于100°,则它的顶角是(?? )
A.?80° 或50°??????????????????????????????B.?20°??????????????????????????????C.?80°或20°??????????????????????????????D.?不能确定
14.在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=12∠B=13∠C; ④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
15.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是(???? )
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?25°???????????????????????????????????????D.?30°
16.如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE= BD;②AG= BF ;③FG∥BE;④OC平分∠BOE,其中结论正确的个数有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(本大题有3个小题,共12分,17-18小题各3分;19小题有3个空,每空2分)
17.如图,已知∠1=∠2,请你添加一个条件________,使得△ABD≌△ACD。(添一个即可)
18.如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=2,则S△AEC等于________。
19.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=64°,则∠A1=________,∠A3=________,若∠A=α,则∠A2018为________。
三、解答题(本大题有7个小题,共66分)
20.已知n边形的内角和θ=(n-2)×180°
(1)当θ=900°时,求出边数n;
(2)小明说θ能取800°,这种说法对吗?若对,求出边数n;若不对,说明理由。
21.已知a,b,c是△ABC的三边长。
(1)若a,b,c满足|a-b|+|b-c|=0,试判断△ABC的形状。
(2)若a,b,c满足(a-b)(b-c)=0,试判断△ABC的形状。
22.琪琪家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,
(1)爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C,D,使CD=________,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段________的长度就是AB的长。
按小明的想法填写题目中的空格;
(2)请完成推理过程。
23.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数。
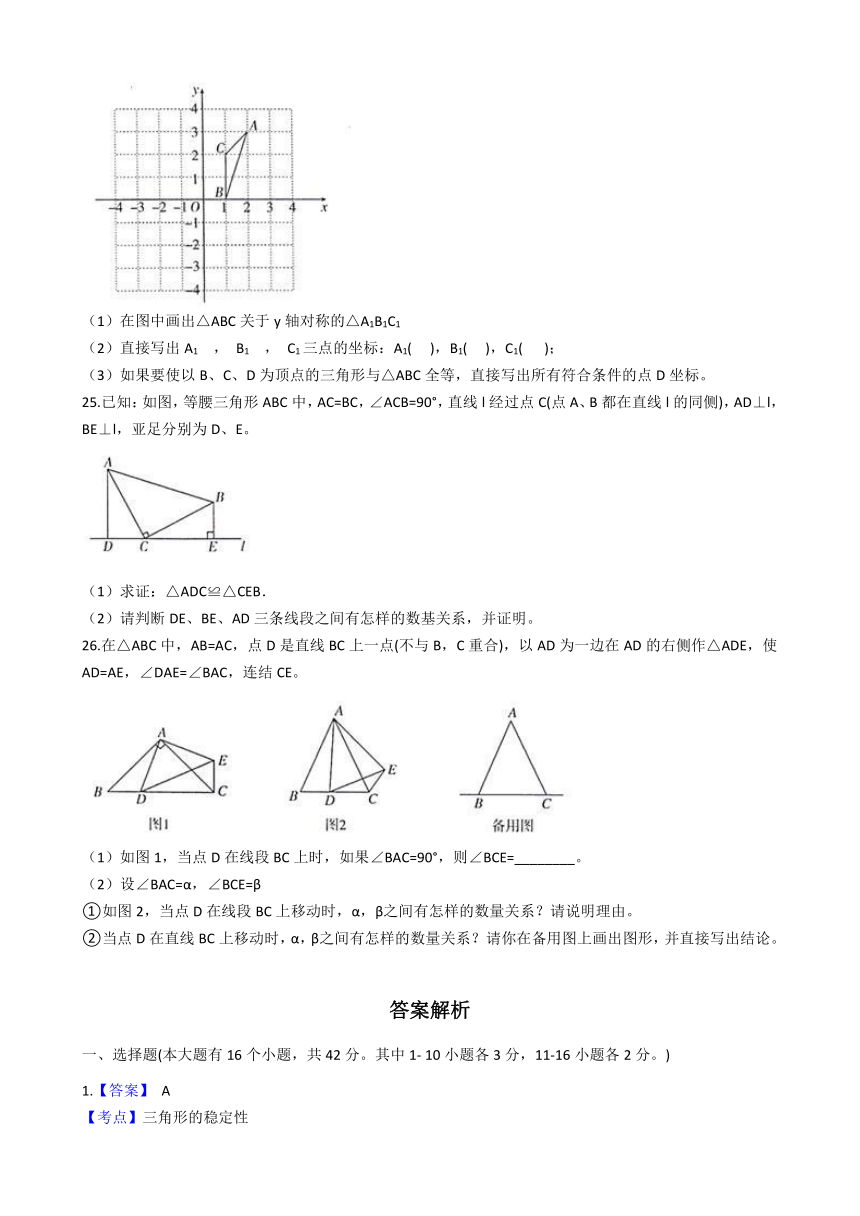
24.如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(2,3) ,B(1,0),C(1,2)。
(1)在图中画出△ABC关于y轴对称的△A1B1C1
(2)直接写出A1 , B1 , C1三点的坐标:A1( ???),B1( ???),C1(???? );
(3)如果要使以B、C、D为顶点的三角形与△ABC全等,直接写出所有符合条件的点D坐标。
25.已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,亚足分别为D、E。
(1)求证:△ADC≌△CEB.
(2)请判断DE、BE、AD三条线段之间有怎样的数基关系,并证明。
26.在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE。
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=________。
(2)设∠BAC=α,∠BCE=β
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由。
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论。
答案解析
一、选择题(本大题有16个小题,共42分。其中1- 10小题各3分,11-16小题各2分。)
1.【答案】 A
【考点】三角形的稳定性
【解析】【解答】因为三角形具有稳定性,而A中全部构成了三角形结构.故选A.
【分析】根据三角形具有稳定性作答.
2.【答案】 C
【考点】轴对称的性质,轴对称图形
【解析】【解答】解:“中”为轴对称图形。
故答案为:C.
【分析】根据轴对称图形的性质进行判断即可得到答案。
3.【答案】 C
【考点】三角形三边关系
【解析】【解答】解:根据题意可知,设第三根木棍的长度为x
则有8-5<x<8+5
即3<x<13
∴符合条件的第三根木棍的长度可以为8
故答案为:C.
【分析】根据三角形三边关系,即可得到第三根木棍的长度范围,解出答案即可。
4.【答案】 A
【考点】三角形的外角性质
【解析】【解答】∵三角形的外角等于与它不相邻的两个内角之和,三角形的一个外角与它不相邻的两个内角的和为 180°
∴2×此外角=180°
此外角=90°
故与此外角相邻的内角为:180°-90°=90°
故答案为:A.
【分析】根据三角形的外角性质和已知条件判断即可.
5.【答案】 D
【考点】三角形的角平分线、中线和高
【解析】【解答】解:三角形的高是过三角形的顶点向对边所作垂线段的长,则图中能表示△ABC的BC边上的高的是AG;
故答案为:D.
【分析】三角形的高是过三角形的顶点向对边所作垂线段的长,故 △ABC 的BC边上的高就应该是过点A向BC所在的直线引垂线段,观察图形即可得出答案.
6.【答案】 B
【考点】三角形的角平分线、中线和高,三角形的面积
【解析】【解答】解:根据题意可知,三角形ABC的高固定
∴将三角形土地进行平分时,底相等即可
∴此时AD为三角形ABC的中线
故答案为:B.
【分析】根据三角形的面积以及中线的性质即可得到答案。
7.【答案】 D
【考点】三角形内角和定理,对顶角及其性质
【解析】【解答】解:∵∠A=∠C=90°,∠AEB=∠GED
∴∠1=∠2=25°
故答案为:D.
【分析】根据三角形的内角和定理以及对顶角相等的性质,即可得到答案。
8.【答案】 C
【考点】角平分线的性质
【解析】【解答】解:如图,过点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA于D,
∴PE=PD,
∵PE=4,
∴PD=4,
故答案为:C.
【分析】如图,过点P作PE⊥OB于点E,根据角平分线的性质可得PE=PD,从而求出结论.
9.【答案】 B
【考点】角平分线的性质
【解析】【解答】第一步:以B为圆心,适当长为半径画弧,分别交射线 BA , BC 于点D,E;
∴ a>0 ;
第二步:分别以D,E为圆心,大于 12DE 的长为半径画弧,两弧在 ∠ABC 内部交于点P;
∴ b>12DE 的长;
第三步:画射线 BP .射线 BP 即为所求.
综上,答案为: a>0 ; b>12DE 的长,
故答案为:B.
【分析】根据作角平分线的方法进行判断,即可得出结论.
10.【答案】 A
【考点】三角形的角平分线、中线和高,三角形三边关系,三角形内角和定理,三角形的外角性质
【解析】【解答】A.三角形的中线、角平分线、高线都是线段,正确;
B.∵若三条线段的长 a 、 b 、 c 满足 a+b>c , b+c>a , a+c>b ,则以 a 、 b 、 c 为边一定能组成三角形,故不正确;
C.∵三角形的外角大于任何一个与它不相邻的内角,故不正确;
D.∵三角形的外角和是 360° ,故不正确.
故答案为:A.
【分析】根据三角形的中线、角平分线和高的定义,三角形三条边的关系,三角形外角与内角的关系,三角形的外角和解答即可..
11.【答案】 D
【考点】线段垂直平分线的性质
【解析】【解答】解:∵MN为线段AB的垂直平分线
∴AD=BD
∴△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC
∵AC=10,BC=6
∴三角形的周长为16
故答案为:D.
【分析】根据线段垂直平分线的性质以及三角形BCD的周长公式,运用等量代换,即可得到三角形BCD的周长为等腰三角形BAC的AC和BC两个边的长度和,求出答案即可。
12.【答案】 D
【考点】平行线的性质,角平分线的性质
【解析】【解答】解:∵BE为∠ABC的平分线
∴∠MBE=∠EBC
∵MN∥BC
∴∠EBC=∠MEB
∴∠MBE=∠MEB
∴BM=ME
同理可得,EN=NC
∴MN=ME+EN=BM+CN=2+3=5
故答案为:D.
【分析】根据角平分线的性质以及平行的性质,等量代换,将MN的长度计算为BM和CN的长度和,即可得到答案。
13.【答案】 C
【考点】三角形的外角性质
【解析】【解答】解:①若已知等腰三角形的一个外角等于100°是顶角的外角,则顶角=180°-100°=80°;
②若已知等腰三角形的一个外角等于100°是底角的外角,则底角=180°-100°=80°,那么顶角=180°-2×80°=20°.
故答案为:C.
【分析】分两种情况考虑:①已知外角是顶角的外角,②已知外角是底角的外角,再结合三角形的内角和为180°,即可求出顶角的度数.
14.【答案】 B
【考点】三角形内角和定理
【解析】【解答】解:①、∵∠A+∠B=∠C=90°,∴△ABC是直角三角形,故小题正确;
②、∵∠A:∠B:∠C=1:2:3,∴∠A=30°,∠B=60°,∠C=90°,△ABC是直角三角形,故本小题正确;
③、设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,解得x=30°,故3x=90°,△ABC是直角三角形,故本小题正确;
④∵设∠C=x,则∠A=∠B=2x,∴2x+2x+x=180°,解得x=36°,∴2x=72°,故本小题错误;
⑤∠A=2∠B=3∠C,
∴∠A+∠B+∠C=∠A+12∠A+13∠A=180°,
∴∠A=108011°,故本小题错误.
综上所述,是直角三角形的是①②③共3个.
故选B.
【分析】根据直角三角形的判定对各个条件进行分析,从而得到答案.
15.【答案】 A
【考点】三角形内角和定理,三角形全等及其性质
【解析】【解答】解:∵△ABC≌△ADE
∴∠B=∠D,∠BAC=∠DAE
∵∠BAD=∠BAC-∠CAD,∠CAE=∠DAE-∠CAD
∴∠BAD=∠CAE
∵∠DAC=70°,∠BAE=100°
∴∠BAD=12(∠BAE-∠DAC)=12(100°-70°)=15°
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD
∴∠DFB=∠BAD=15°
故答案为:A.
【分析】根据全等三角形的性质计算得到∠B=∠D,∠BAC=∠DAE,求出∠BAD的度数之后,根据三角形的内角和为180°,即可得到答案。
16.【答案】 D
【考点】三角形全等及其性质,等边三角形的判定与性质
【解析】【解答】解:∵△ABC和△DCE均为等边三角形
∴BC=AC,CD=CE,∠ACB=∠ECD=60°
∴∠ACB+∠ACD=∠ACD+∠ECD=∠ACD=60°
∴△BCD≌△ACE
所以AEBD,即①正确;
∵∠CBD=∠CAE,∠BCA=∠ACG=60°,AC=BC
∴△BCF≌△ACG
∴AG=BF,②正确;
同理可得,△DFC≌△EGC
∴CF=CG
∴△CFG为等边三角形
∴∠CFG=∠FCB=60°
∴FC∥BE,即③正确;
过点C作CM⊥AE于M,CN⊥BD于N
∵△BCD≌△ACE
∴∠BDC=∠AEC
∵CD=CE,∠CND=∠CMA=90°
∴△CDN≌△CEM
∴CM=CN
∵CM⊥AE,CN⊥BD
∴Rt△OCN≌Rt△OCM
∴∠BOC=∠EOC
∴OC平分∠BOE,即④正确
故答案为:D.
【分析】根据等边三角形的性质,判断得到△BCD≌△ACE,继而由全等三角形的性质分别进行证明判断即可得到答案。
二、填空题(本大题有3个小题,共12分,17-18小题各3分;19小题有3个空,每空2分)
17.【答案】 AB=AC(答案不唯一)
【考点】三角形全等的判定
【解析】【解答】解:添加条件为AB=AC
∵∠1=∠2,AB=AC,AD=AD
∴△ABD≌△ACD
【分析】根据三角形全等的判定和性质,添加合适的条件即可。
18.【答案】 16
【考点】三角形的角平分线、中线和高,三角形的面积
【解析】【解答】解:∵三角形的中线将三角形分为两个相等的部分
又∵CE为△ACD的中线,DF为△CDE的中线,AD为△ABC的中线
∴S△CDE=2S△DEF=4
∴S△ACD=2S△CDE=8
∴S△ABC=2S△ACD=16
【分析】根据三角形中线的性质以及三角形的面积公式,表示出各个三角形之间的数量关系,即可得到答案。
19.【答案】 32°;8°;α22018
【考点】三角形的外角性质,角平分线的性质
【解析】【解答】解:∵A1B为∠ABC的角平分线,A1C为∠ACD的角平分线
∴∠A1BC=12∠ABC,∠A1CD=12∠ACD
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1
∴12(∠A+∠ABC)=12∠ABC+12∠A1
∴∠A1=12∠A
∵∠A=α
∴∠A1=12α
同理,∠A2=12∠A1=122α
∴∠A2018=α22018
当∠A=64°时,∠A1=32°,∠A3=8
【分析】根据角平分线的性质以及三角形外角的性质,即可得到∠A1=12α,同理即可得到∠A2=12∠A1=122α,以此类推即可得到后一个角为前一个角的12 , 即可得到规律,计算得到答案即可。
三、解答题(本大题有7个小题,共66分)
20.【答案】 (1)解:900°=(n-2) ×180°, 整理得n-2=5,解得n=7
(2)解:小明的说法不对,理由如下:当θ取800°时,800°=(n-2)×180°, 解得n= 589
∵n为正整数,∴θ不能取800°
【考点】多边形内角与外角
【解析】【分析】(1)根据题目中n边形的内角和,令 θ =900°,即可得到n的值;
(2)令 θ =800°,根据n的得数判断其说法是否正确即可。
21.【答案】 (1)解:∵|a-b|+|b-c|=0,
∴a-b=0且b-c=0
∴a=b=c
∴△ABC为等边三角形
(2)解:∵(a-b)(b-c)=0,
∴a-b=0或b-c=0
∴a=b或b=c.
∴△ABC为等腰三角形
【考点】绝对值的非负性,三角形相关概念
【解析】【分析】(1)根据绝对值的非负性,即可得到a=b=c,即可得到三角形的形状为等边三角形;
(2)根据题意,即可得到a=b或b=c,即可判断三角形的形状。
22.【答案】 (1)CB;DE
(2)解:由题意得DG⊥BF,
∴∠CDE=∠CBA=90° ,
在△ABC和△EDC中, {∠CDE=∠CBACB=CD∠ACB=∠ECD
∴△ABC≌△EDC(ASA),
∴DE=AB (全等三角形的对应边相等)
【考点】全等三角形的应用
【解析】【分析】(1)根据题意,由描述得到线段相等即可;
(2)根据题意,由三角形全等的判定和性质计算得到DE=AB即可得到答案。
23.【答案】 解:∵在△ABC中,AD是高,
∴∠ADC= 90° ,
∵在△ACD中,∠C=50°,
∴∠DAC=90°-50°=40°,
∵在△ABC中,∠C=50°,∠BAC=60° ,
∴∠ABC=70°,
∵在△ABC中,AE,BF分别是∠BAC和∠ABC的角平分线,
∴∠EAC= 12 ∠BAC=30° ,∠FBC= 12 ∠ABC=35°,
∴∠BOA=∠BEA+∠FBC=∠C+∠EAC+∠FBC=50°+30°+35°=115°
【考点】三角形内角和定理,角平分线的性质
【解析】【分析】根据题意,由三角形的内角和定理计算得到∠DAC的度数,同理即可得到∠ABC的度数,继而根据角平分线的性质求出∠EAC以及∠FBC的度数,计算得到∠BOA的度数即可。
24.【答案】 (1)解:如图1,△A1B1C1 即为所求:
(2)解:由(1)可知:A1(-2,3)B1(-1,0)C1(-1,2)
(3)解:如图2所示,点D的坐标为(0,-1)或(2,-1)或(0,3)
【考点】三角形全等及其性质,三角形全等的判定,关于坐标轴对称的点的坐标特征,作图﹣轴对称
【解析】【分析】(1)关于y轴对称的点的坐标,横坐标互为相反数,纵坐标不变,首先做三角形ABC三个顶点关于y轴的对称点,再连线即可得到三角形;
(2)根据作出的对称图形,直接得到三角形三个顶点的距离即可;
(3)根据三角形全等的判定和性质,作出符合条件的D点的坐标即可。
25.【答案】 (1)证明:∵AD⊥I,BE⊥I,∠ACB=90°,
∴∠ADC=∠ACB=∠CEB=90°,
∴∠DAC+∠DCA= 90°
∠DCA+∠ECB=180°-90°=90° ,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
{∠ADC=∠CEB∠DAC=∠ECBAC=BC
∴△ADC≌△CEB (AAS
(2)解: DE=AD+ BE
证明:∵△ADC≌△CEB
∴AD=CE ?DC=EB
∵DE=CE+DC
∴DE=AD+ BE
【考点】三角形内角和定理,三角形全等及其性质,三角形全等的判定
【解析】【分析】(1)根据题意,由垂直的性质以及三角形的内角和定理,即可得到△ADC≌△CEB;
(2)根据(1)中的△ADC≌△CEB,由全等三角形的性质,根据等量代换即可得到DE=AD+BE。
26.【答案】 (1)90°
(2)解:①由(1)中可知=180”-α
∴αβ存在的数量关系为α+β=180°
证明方法同(1)中证明
②当点D在射线BC上时,如图1
同(1)的方法即可得出,△ABD≌△ACE (SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=180°-∠BAC=180°-a,
∴α+β=180°;
当点D在射线BC的反向延长线上时,如图2,
同(1)的方法即可得出,△ABD≌△ACE (SAS);
∴∠ABD= LACE,
∴β=∠BCE=∠ACE-∠ACB=∠ABD-∠ACB=∠BAC=α,
∴α=β
【考点】三角形全等及其性质,三角形全等的判定
【解析】【解答】(1)证明:∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC; .
∴∠CAE=∠BAD;
在△ABD和△ACE中, {AB=AC∠BAD=∠CAEAD=AE
∴△ABD≌△ACE (SAS):
∴∠B=∠ACE
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°-∠BAC=90° ;
故答案为90°
【分析】(1)根据题意,证明得到△BAD≌△CAE,即可得到∠B=∠ACE,,证明得到∠ACB=45°,即可得到答案;
(2)①根据(1)中的△BAD≌△CAE,根据三角形全等的性质,即可得到答案;
②同理根据△BAD≌△CAE,结合三角形全等的性质以及三角形外角的性质即可得到答案。
一、选择题(本大题有16个小题,共42分。其中1- 10小题各3分,11-16小题各2分)
1.下列各图形中,具有稳定性的是( )
A.????????????????????????B.????????????????????????C.????????????????????????D.?
2.现实世界中,对称现象无处不在,中国的方块字中有的也具有对称性,下列汉字是轴对称图形的是( ???)
A.?爱?????????????????????????????????????????B.?我?????????????????????????????????????????C.?中?????????????????????????????????????????D.?华
3.小晶有两根长度为5cm、8cm的木条,她想钉一个三角形的木框,现在有长度分别为2cm、3cm、8cm、15cm的木条供她选择,那她第三根应选择( ???)
A.?2cm????????????????????????????????????B.?3cm????????????????????????????????????C.?8cm????????????????????????????????????D.?15cm
4.如果三角形的一个外角与它不相邻的两个内角的和为 180° ,那么这个三角形是(??? )
A.?直角三角形????????????????????????B.?钝角三角形????????????????????????C.?锐角三角形????????????????????????D.?无法确定
5.图中能表示 △ABC 的BC边上的高的是 ( ??? )
A.???????????????????B.???????????????????C.???????????????????D.?
6.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( ???)
A.?角平分线????????????????????????????????B.?中线????????????????????????????????C.?高????????????????????????????????D.?任意一条线
7.如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为( ???)
A.?55°???????????????????????????????????????B.?35°???????????????????????????????????????C.?45°???????????????????????????????????????D.?25°
8.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,点P到边OB的距离为4,则PD=(?? )
A.?6???????????????????????????????????????????B.?5???????????????????????????????????????????C.?4???????????????????????????????????????????D.?3
9.如图1,已知 ∠ABC ,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线 BA , BC 于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在 ∠ABC 内部交于点P;
第三步:画射线 BP .射线 BP 即为所求.
下列正确的是(??? )
A.?a,b均无限制?????????????????????????????????????????????????????B.?a>0 , b>12DE 的长
C.?a有最小限制,b无限制???????????????????????????????????????D.?a≥0 , b<12DE 的长
10.下列说法正确的是(??????? )
A.?三角形的中线、角平分线和高都是线段;
B.?若三条线段的长 a 、 b 、 c 满足 a+b>c ,则以 a 、 b 、 c 为边一定能组成三角形;
C.?三角形的外角大于它的任何一个内角;
D.?三角形的外角和是 180° .
11.如图,等腰△ABC中,AB=AC= 10,BC=6,直线MN垂直平分AB交AC于D,连接BD,则△BCD的周长等于( ???)
A.?13?????????????????????????????????????????B.?14?????????????????????????????????????????C.?15?????????????????????????????????????????D.?16
12.如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM=2,CN=3,则MN的长为( ???)
A.?10??????????????????????????????????????????B.?5.5??????????????????????????????????????????C.?6??????????????????????????????????????????D.?5
13.已知等腰三角形的一个外角等于100°,则它的顶角是(?? )
A.?80° 或50°??????????????????????????????B.?20°??????????????????????????????C.?80°或20°??????????????????????????????D.?不能确定
14.在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=12∠B=13∠C; ④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )
A.?2个???????????????????????????????????????B.?3个???????????????????????????????????????C.?4个???????????????????????????????????????D.?5个
15.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是(???? )
A.?15°???????????????????????????????????????B.?20°???????????????????????????????????????C.?25°???????????????????????????????????????D.?30°
16.如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE= BD;②AG= BF ;③FG∥BE;④OC平分∠BOE,其中结论正确的个数有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
二、填空题(本大题有3个小题,共12分,17-18小题各3分;19小题有3个空,每空2分)
17.如图,已知∠1=∠2,请你添加一个条件________,使得△ABD≌△ACD。(添一个即可)
18.如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=2,则S△AEC等于________。
19.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=64°,则∠A1=________,∠A3=________,若∠A=α,则∠A2018为________。
三、解答题(本大题有7个小题,共66分)
20.已知n边形的内角和θ=(n-2)×180°
(1)当θ=900°时,求出边数n;
(2)小明说θ能取800°,这种说法对吗?若对,求出边数n;若不对,说明理由。
21.已知a,b,c是△ABC的三边长。
(1)若a,b,c满足|a-b|+|b-c|=0,试判断△ABC的形状。
(2)若a,b,c满足(a-b)(b-c)=0,试判断△ABC的形状。
22.琪琪家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,
(1)爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C,D,使CD=________,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段________的长度就是AB的长。
按小明的想法填写题目中的空格;
(2)请完成推理过程。
23.如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数。
24.如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(2,3) ,B(1,0),C(1,2)。
(1)在图中画出△ABC关于y轴对称的△A1B1C1
(2)直接写出A1 , B1 , C1三点的坐标:A1( ???),B1( ???),C1(???? );
(3)如果要使以B、C、D为顶点的三角形与△ABC全等,直接写出所有符合条件的点D坐标。
25.已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,亚足分别为D、E。
(1)求证:△ADC≌△CEB.
(2)请判断DE、BE、AD三条线段之间有怎样的数基关系,并证明。
26.在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE。
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=________。
(2)设∠BAC=α,∠BCE=β
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由。
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论。
答案解析
一、选择题(本大题有16个小题,共42分。其中1- 10小题各3分,11-16小题各2分。)
1.【答案】 A
【考点】三角形的稳定性
【解析】【解答】因为三角形具有稳定性,而A中全部构成了三角形结构.故选A.
【分析】根据三角形具有稳定性作答.
2.【答案】 C
【考点】轴对称的性质,轴对称图形
【解析】【解答】解:“中”为轴对称图形。
故答案为:C.
【分析】根据轴对称图形的性质进行判断即可得到答案。
3.【答案】 C
【考点】三角形三边关系
【解析】【解答】解:根据题意可知,设第三根木棍的长度为x
则有8-5<x<8+5
即3<x<13
∴符合条件的第三根木棍的长度可以为8
故答案为:C.
【分析】根据三角形三边关系,即可得到第三根木棍的长度范围,解出答案即可。
4.【答案】 A
【考点】三角形的外角性质
【解析】【解答】∵三角形的外角等于与它不相邻的两个内角之和,三角形的一个外角与它不相邻的两个内角的和为 180°
∴2×此外角=180°
此外角=90°
故与此外角相邻的内角为:180°-90°=90°
故答案为:A.
【分析】根据三角形的外角性质和已知条件判断即可.
5.【答案】 D
【考点】三角形的角平分线、中线和高
【解析】【解答】解:三角形的高是过三角形的顶点向对边所作垂线段的长,则图中能表示△ABC的BC边上的高的是AG;
故答案为:D.
【分析】三角形的高是过三角形的顶点向对边所作垂线段的长,故 △ABC 的BC边上的高就应该是过点A向BC所在的直线引垂线段,观察图形即可得出答案.
6.【答案】 B
【考点】三角形的角平分线、中线和高,三角形的面积
【解析】【解答】解:根据题意可知,三角形ABC的高固定
∴将三角形土地进行平分时,底相等即可
∴此时AD为三角形ABC的中线
故答案为:B.
【分析】根据三角形的面积以及中线的性质即可得到答案。
7.【答案】 D
【考点】三角形内角和定理,对顶角及其性质
【解析】【解答】解:∵∠A=∠C=90°,∠AEB=∠GED
∴∠1=∠2=25°
故答案为:D.
【分析】根据三角形的内角和定理以及对顶角相等的性质,即可得到答案。
8.【答案】 C
【考点】角平分线的性质
【解析】【解答】解:如图,过点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA于D,
∴PE=PD,
∵PE=4,
∴PD=4,
故答案为:C.
【分析】如图,过点P作PE⊥OB于点E,根据角平分线的性质可得PE=PD,从而求出结论.
9.【答案】 B
【考点】角平分线的性质
【解析】【解答】第一步:以B为圆心,适当长为半径画弧,分别交射线 BA , BC 于点D,E;
∴ a>0 ;
第二步:分别以D,E为圆心,大于 12DE 的长为半径画弧,两弧在 ∠ABC 内部交于点P;
∴ b>12DE 的长;
第三步:画射线 BP .射线 BP 即为所求.
综上,答案为: a>0 ; b>12DE 的长,
故答案为:B.
【分析】根据作角平分线的方法进行判断,即可得出结论.
10.【答案】 A
【考点】三角形的角平分线、中线和高,三角形三边关系,三角形内角和定理,三角形的外角性质
【解析】【解答】A.三角形的中线、角平分线、高线都是线段,正确;
B.∵若三条线段的长 a 、 b 、 c 满足 a+b>c , b+c>a , a+c>b ,则以 a 、 b 、 c 为边一定能组成三角形,故不正确;
C.∵三角形的外角大于任何一个与它不相邻的内角,故不正确;
D.∵三角形的外角和是 360° ,故不正确.
故答案为:A.
【分析】根据三角形的中线、角平分线和高的定义,三角形三条边的关系,三角形外角与内角的关系,三角形的外角和解答即可..
11.【答案】 D
【考点】线段垂直平分线的性质
【解析】【解答】解:∵MN为线段AB的垂直平分线
∴AD=BD
∴△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC
∵AC=10,BC=6
∴三角形的周长为16
故答案为:D.
【分析】根据线段垂直平分线的性质以及三角形BCD的周长公式,运用等量代换,即可得到三角形BCD的周长为等腰三角形BAC的AC和BC两个边的长度和,求出答案即可。
12.【答案】 D
【考点】平行线的性质,角平分线的性质
【解析】【解答】解:∵BE为∠ABC的平分线
∴∠MBE=∠EBC
∵MN∥BC
∴∠EBC=∠MEB
∴∠MBE=∠MEB
∴BM=ME
同理可得,EN=NC
∴MN=ME+EN=BM+CN=2+3=5
故答案为:D.
【分析】根据角平分线的性质以及平行的性质,等量代换,将MN的长度计算为BM和CN的长度和,即可得到答案。
13.【答案】 C
【考点】三角形的外角性质
【解析】【解答】解:①若已知等腰三角形的一个外角等于100°是顶角的外角,则顶角=180°-100°=80°;
②若已知等腰三角形的一个外角等于100°是底角的外角,则底角=180°-100°=80°,那么顶角=180°-2×80°=20°.
故答案为:C.
【分析】分两种情况考虑:①已知外角是顶角的外角,②已知外角是底角的外角,再结合三角形的内角和为180°,即可求出顶角的度数.
14.【答案】 B
【考点】三角形内角和定理
【解析】【解答】解:①、∵∠A+∠B=∠C=90°,∴△ABC是直角三角形,故小题正确;
②、∵∠A:∠B:∠C=1:2:3,∴∠A=30°,∠B=60°,∠C=90°,△ABC是直角三角形,故本小题正确;
③、设∠A=x,∠B=2x,∠C=3x,则x+2x+3x=180°,解得x=30°,故3x=90°,△ABC是直角三角形,故本小题正确;
④∵设∠C=x,则∠A=∠B=2x,∴2x+2x+x=180°,解得x=36°,∴2x=72°,故本小题错误;
⑤∠A=2∠B=3∠C,
∴∠A+∠B+∠C=∠A+12∠A+13∠A=180°,
∴∠A=108011°,故本小题错误.
综上所述,是直角三角形的是①②③共3个.
故选B.
【分析】根据直角三角形的判定对各个条件进行分析,从而得到答案.
15.【答案】 A
【考点】三角形内角和定理,三角形全等及其性质
【解析】【解答】解:∵△ABC≌△ADE
∴∠B=∠D,∠BAC=∠DAE
∵∠BAD=∠BAC-∠CAD,∠CAE=∠DAE-∠CAD
∴∠BAD=∠CAE
∵∠DAC=70°,∠BAE=100°
∴∠BAD=12(∠BAE-∠DAC)=12(100°-70°)=15°
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD
∴∠DFB=∠BAD=15°
故答案为:A.
【分析】根据全等三角形的性质计算得到∠B=∠D,∠BAC=∠DAE,求出∠BAD的度数之后,根据三角形的内角和为180°,即可得到答案。
16.【答案】 D
【考点】三角形全等及其性质,等边三角形的判定与性质
【解析】【解答】解:∵△ABC和△DCE均为等边三角形
∴BC=AC,CD=CE,∠ACB=∠ECD=60°
∴∠ACB+∠ACD=∠ACD+∠ECD=∠ACD=60°
∴△BCD≌△ACE
所以AEBD,即①正确;
∵∠CBD=∠CAE,∠BCA=∠ACG=60°,AC=BC
∴△BCF≌△ACG
∴AG=BF,②正确;
同理可得,△DFC≌△EGC
∴CF=CG
∴△CFG为等边三角形
∴∠CFG=∠FCB=60°
∴FC∥BE,即③正确;
过点C作CM⊥AE于M,CN⊥BD于N
∵△BCD≌△ACE
∴∠BDC=∠AEC
∵CD=CE,∠CND=∠CMA=90°
∴△CDN≌△CEM
∴CM=CN
∵CM⊥AE,CN⊥BD
∴Rt△OCN≌Rt△OCM
∴∠BOC=∠EOC
∴OC平分∠BOE,即④正确
故答案为:D.
【分析】根据等边三角形的性质,判断得到△BCD≌△ACE,继而由全等三角形的性质分别进行证明判断即可得到答案。
二、填空题(本大题有3个小题,共12分,17-18小题各3分;19小题有3个空,每空2分)
17.【答案】 AB=AC(答案不唯一)
【考点】三角形全等的判定
【解析】【解答】解:添加条件为AB=AC
∵∠1=∠2,AB=AC,AD=AD
∴△ABD≌△ACD
【分析】根据三角形全等的判定和性质,添加合适的条件即可。
18.【答案】 16
【考点】三角形的角平分线、中线和高,三角形的面积
【解析】【解答】解:∵三角形的中线将三角形分为两个相等的部分
又∵CE为△ACD的中线,DF为△CDE的中线,AD为△ABC的中线
∴S△CDE=2S△DEF=4
∴S△ACD=2S△CDE=8
∴S△ABC=2S△ACD=16
【分析】根据三角形中线的性质以及三角形的面积公式,表示出各个三角形之间的数量关系,即可得到答案。
19.【答案】 32°;8°;α22018
【考点】三角形的外角性质,角平分线的性质
【解析】【解答】解:∵A1B为∠ABC的角平分线,A1C为∠ACD的角平分线
∴∠A1BC=12∠ABC,∠A1CD=12∠ACD
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1
∴12(∠A+∠ABC)=12∠ABC+12∠A1
∴∠A1=12∠A
∵∠A=α
∴∠A1=12α
同理,∠A2=12∠A1=122α
∴∠A2018=α22018
当∠A=64°时,∠A1=32°,∠A3=8
【分析】根据角平分线的性质以及三角形外角的性质,即可得到∠A1=12α,同理即可得到∠A2=12∠A1=122α,以此类推即可得到后一个角为前一个角的12 , 即可得到规律,计算得到答案即可。
三、解答题(本大题有7个小题,共66分)
20.【答案】 (1)解:900°=(n-2) ×180°, 整理得n-2=5,解得n=7
(2)解:小明的说法不对,理由如下:当θ取800°时,800°=(n-2)×180°, 解得n= 589
∵n为正整数,∴θ不能取800°
【考点】多边形内角与外角
【解析】【分析】(1)根据题目中n边形的内角和,令 θ =900°,即可得到n的值;
(2)令 θ =800°,根据n的得数判断其说法是否正确即可。
21.【答案】 (1)解:∵|a-b|+|b-c|=0,
∴a-b=0且b-c=0
∴a=b=c
∴△ABC为等边三角形
(2)解:∵(a-b)(b-c)=0,
∴a-b=0或b-c=0
∴a=b或b=c.
∴△ABC为等腰三角形
【考点】绝对值的非负性,三角形相关概念
【解析】【分析】(1)根据绝对值的非负性,即可得到a=b=c,即可得到三角形的形状为等边三角形;
(2)根据题意,即可得到a=b或b=c,即可判断三角形的形状。
22.【答案】 (1)CB;DE
(2)解:由题意得DG⊥BF,
∴∠CDE=∠CBA=90° ,
在△ABC和△EDC中, {∠CDE=∠CBACB=CD∠ACB=∠ECD
∴△ABC≌△EDC(ASA),
∴DE=AB (全等三角形的对应边相等)
【考点】全等三角形的应用
【解析】【分析】(1)根据题意,由描述得到线段相等即可;
(2)根据题意,由三角形全等的判定和性质计算得到DE=AB即可得到答案。
23.【答案】 解:∵在△ABC中,AD是高,
∴∠ADC= 90° ,
∵在△ACD中,∠C=50°,
∴∠DAC=90°-50°=40°,
∵在△ABC中,∠C=50°,∠BAC=60° ,
∴∠ABC=70°,
∵在△ABC中,AE,BF分别是∠BAC和∠ABC的角平分线,
∴∠EAC= 12 ∠BAC=30° ,∠FBC= 12 ∠ABC=35°,
∴∠BOA=∠BEA+∠FBC=∠C+∠EAC+∠FBC=50°+30°+35°=115°
【考点】三角形内角和定理,角平分线的性质
【解析】【分析】根据题意,由三角形的内角和定理计算得到∠DAC的度数,同理即可得到∠ABC的度数,继而根据角平分线的性质求出∠EAC以及∠FBC的度数,计算得到∠BOA的度数即可。
24.【答案】 (1)解:如图1,△A1B1C1 即为所求:
(2)解:由(1)可知:A1(-2,3)B1(-1,0)C1(-1,2)
(3)解:如图2所示,点D的坐标为(0,-1)或(2,-1)或(0,3)
【考点】三角形全等及其性质,三角形全等的判定,关于坐标轴对称的点的坐标特征,作图﹣轴对称
【解析】【分析】(1)关于y轴对称的点的坐标,横坐标互为相反数,纵坐标不变,首先做三角形ABC三个顶点关于y轴的对称点,再连线即可得到三角形;
(2)根据作出的对称图形,直接得到三角形三个顶点的距离即可;
(3)根据三角形全等的判定和性质,作出符合条件的D点的坐标即可。
25.【答案】 (1)证明:∵AD⊥I,BE⊥I,∠ACB=90°,
∴∠ADC=∠ACB=∠CEB=90°,
∴∠DAC+∠DCA= 90°
∠DCA+∠ECB=180°-90°=90° ,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
{∠ADC=∠CEB∠DAC=∠ECBAC=BC
∴△ADC≌△CEB (AAS
(2)解: DE=AD+ BE
证明:∵△ADC≌△CEB
∴AD=CE ?DC=EB
∵DE=CE+DC
∴DE=AD+ BE
【考点】三角形内角和定理,三角形全等及其性质,三角形全等的判定
【解析】【分析】(1)根据题意,由垂直的性质以及三角形的内角和定理,即可得到△ADC≌△CEB;
(2)根据(1)中的△ADC≌△CEB,由全等三角形的性质,根据等量代换即可得到DE=AD+BE。
26.【答案】 (1)90°
(2)解:①由(1)中可知=180”-α
∴αβ存在的数量关系为α+β=180°
证明方法同(1)中证明
②当点D在射线BC上时,如图1
同(1)的方法即可得出,△ABD≌△ACE (SAS);
∴∠ABD=∠ACE,
∴β=∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=180°-∠BAC=180°-a,
∴α+β=180°;
当点D在射线BC的反向延长线上时,如图2,
同(1)的方法即可得出,△ABD≌△ACE (SAS);
∴∠ABD= LACE,
∴β=∠BCE=∠ACE-∠ACB=∠ABD-∠ACB=∠BAC=α,
∴α=β
【考点】三角形全等及其性质,三角形全等的判定
【解析】【解答】(1)证明:∵∠DAE=∠BAC,
∴∠DAE-∠DAC=∠BAC-∠DAC; .
∴∠CAE=∠BAD;
在△ABD和△ACE中, {AB=AC∠BAD=∠CAEAD=AE
∴△ABD≌△ACE (SAS):
∴∠B=∠ACE
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°-∠BAC=90° ;
故答案为90°
【分析】(1)根据题意,证明得到△BAD≌△CAE,即可得到∠B=∠ACE,,证明得到∠ACB=45°,即可得到答案;
(2)①根据(1)中的△BAD≌△CAE,根据三角形全等的性质,即可得到答案;
②同理根据△BAD≌△CAE,结合三角形全等的性质以及三角形外角的性质即可得到答案。
同课章节目录
