沪教版(上海)数学八年级下册-20.2 一次函数-用待定系数法求一次函数解析式 教案
文档属性
| 名称 | 沪教版(上海)数学八年级下册-20.2 一次函数-用待定系数法求一次函数解析式 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 29.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 07:49:36 | ||
图片预览

文档简介
一次函数
--用待定系数法求一次函数解析式教学设计
教学目标
【知识与技能】
学会用待定系数法确定一次函数的解析式;用数形结合、看图找信息的方法求一次函数的解析式.
【过程与方法】
经历用待定系数法求解问题的过程,提高解决问题的能力;体验数形结合的思想,运用看图读信息的方法来解决问题.
【情感、态度与价值观】
通过让学生经历先设出未知数,根据题意列出方程再求解的过程,带领学生学习待定系数法,激发学生探索、总结数学方法的兴趣.
重点难点
【重点】
用待定系数法求一次函数的解析式.
【难点】
结合图象求解析式.
教学过程
一、创设情境,导入新知
画出
y=2x
和
y=-1.5x+3
的图象
你在作这两个函数图象时
,分别描了几个点?可以有不同取法吗?
由y=kx+b-满足条件的两定点(x1.y1)
(x2,y2)--
画出--一次函数图像l
这是从数到形的过程
那么如果知道一次函数的图像,要你写出函数解析式该怎样呢?---
用待定系数法求函数解析式
二、共同探究,获取新知
教师多媒体出示:
1.利用图像求函数的解析式
学生讨论.
师:一次函数的形式是什么?有几个常量?哪几个
生:y=kx+b(k、b是常数,k≠0).两个.分别是k和b
师:求两个量需要几个方程?
生:两个.
2.分析与思考
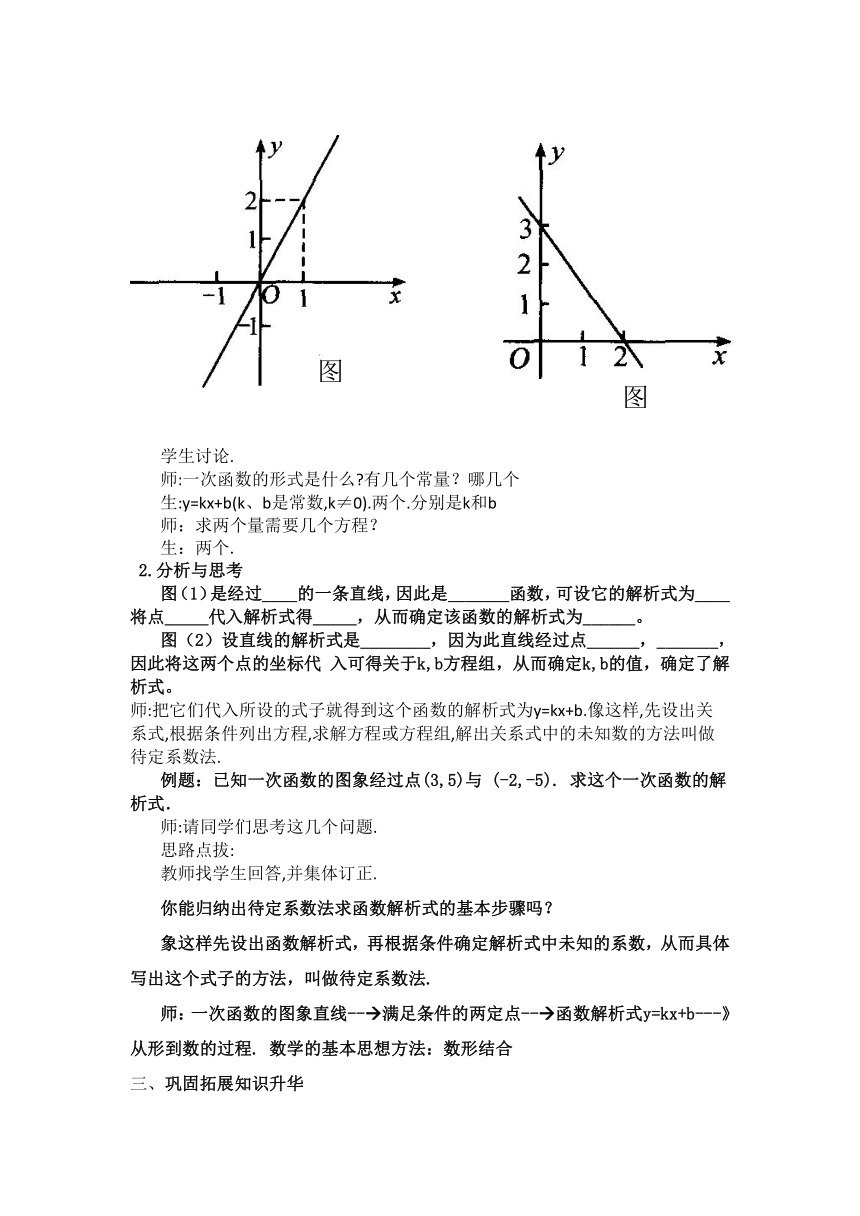
图(1)是经过____的一条直线,因此是_______函数,可设它的解析式为____将点_____代入解析式得_____,从而确定该函数的解析式为______。
图(2)设直线的解析式是________,因为此直线经过点______,_______,因此将这两个点的坐标代
入可得关于k,b方程组,从而确定k,b的值,确定了解析式。
师:把它们代入所设的式子就得到这个函数的解析式为y=kx+b.像这样,先设出关系式,根据条件列出方程,求解方程或方程组,解出关系式中的未知数的方法叫做待定系数法.
例题:已知一次函数的图象经过点(3,5)与
(-2,-5).
求这个一次函数的解析式.
师:请同学们思考这几个问题.
思路点拔:
教师找学生回答,并集体订正.
你能归纳出待定系数法求函数解析式的基本步骤吗?
象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
师:一次函数的图象直线--满足条件的两定点--函数解析式y=kx+b---》从形到数的过程.
数学的基本思想方法:数形结合
三、巩固拓展知识升华
教师多媒体出示:
1.利用点的坐标求函数解析式
已知一条直线与x轴交点的横坐标为-1,与y轴交点的纵坐标为-3,求这条直线的解析式.
请同学们根据这个图象特征写出这条直线所代表的一次函数的解析式.
学生讨论.
教师提示:由图象我们能看出图象经过了哪两个点?
生:(-1,0)和(0,-3)这两点.
教师找一名学生板演,其余学生在下面做,然后集体订正.
?
解:设这条直线解析式为:y=kx+b,由题意知,其图像过(-1,0),(0,-3)得方程组
-k+b=0
b=-3
?
解得K=-3
b=-3
?
这条直线解析式为:y=-3x-3
2.利用表格信息确定函数解析式
小明根据某个一次函数关系式填写了下表:
x
-2
-1
0
1
y
3
?
1
0
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?
?
解:设这条直线解析式为:y=kx+b,由题意知,其图像过(0,1),(1,0)得方程组b=1
k+b=0
解得:k=-1
b=1
?
这条直线解析式为:y=-x+1
?
所以当x=-1时y=-1
(-1)+1=2
?
即墨迹下应是2
3.利用已知的规律等求函数解析式
已知一条直线于直线y=2x平行,且与y轴交点的纵坐标为
-
-3,则其解析式为_________
师:平行直线解析式有何特征?什么叫截距?
生:k相同的直线互相平行;直线与y轴相交时交点的纵坐标读数叫截距.
四、反思总结
师:
确定正比例函数的解析式y=kx,需求哪个值?需要几个条件?
确定一次函数的解析式y=kx+b,需求哪个值?需要几个条件?
学生回答,教师补充完善.
总结:在确定函数解析式时,要求几个系数就需要知道几个条件。
求函数解析式的一般步骤是怎样的呢?
可归纳为:“一设、二列、三解、四还原”
(一)设:设出函数关系式的一般形式y=kx+b
(二)列:根据已知两点的坐标列出关于k、b的二元
一次方程组;
(三)解:解这个方程组,求出k、b的值;
(四)还原:把求得的k、b的值代入y=kx+b,写出函
数关系式.
五
求一次函数关系式常见题型:
1.利用图像求函数关系式
2.利用点的坐标求函数关系式
六
课外选作
1.若一次函数的图象经过点
A(2,0)且与直线y=-x+3平行,求其解析式
2.若一次函数的图象与直线y=-3x+2交y轴于同一点,且过点(2,-6),求此函数解析式
七,课外作业:课本p40练习1,2,
?
P47-48习题12.2
第9,10题
图1
图2
--用待定系数法求一次函数解析式教学设计
教学目标
【知识与技能】
学会用待定系数法确定一次函数的解析式;用数形结合、看图找信息的方法求一次函数的解析式.
【过程与方法】
经历用待定系数法求解问题的过程,提高解决问题的能力;体验数形结合的思想,运用看图读信息的方法来解决问题.
【情感、态度与价值观】
通过让学生经历先设出未知数,根据题意列出方程再求解的过程,带领学生学习待定系数法,激发学生探索、总结数学方法的兴趣.
重点难点
【重点】
用待定系数法求一次函数的解析式.
【难点】
结合图象求解析式.
教学过程
一、创设情境,导入新知
画出
y=2x
和
y=-1.5x+3
的图象
你在作这两个函数图象时
,分别描了几个点?可以有不同取法吗?
由y=kx+b-满足条件的两定点(x1.y1)
(x2,y2)--
画出--一次函数图像l
这是从数到形的过程
那么如果知道一次函数的图像,要你写出函数解析式该怎样呢?---
用待定系数法求函数解析式
二、共同探究,获取新知
教师多媒体出示:
1.利用图像求函数的解析式
学生讨论.
师:一次函数的形式是什么?有几个常量?哪几个
生:y=kx+b(k、b是常数,k≠0).两个.分别是k和b
师:求两个量需要几个方程?
生:两个.
2.分析与思考
图(1)是经过____的一条直线,因此是_______函数,可设它的解析式为____将点_____代入解析式得_____,从而确定该函数的解析式为______。
图(2)设直线的解析式是________,因为此直线经过点______,_______,因此将这两个点的坐标代
入可得关于k,b方程组,从而确定k,b的值,确定了解析式。
师:把它们代入所设的式子就得到这个函数的解析式为y=kx+b.像这样,先设出关系式,根据条件列出方程,求解方程或方程组,解出关系式中的未知数的方法叫做待定系数法.
例题:已知一次函数的图象经过点(3,5)与
(-2,-5).
求这个一次函数的解析式.
师:请同学们思考这几个问题.
思路点拔:
教师找学生回答,并集体订正.
你能归纳出待定系数法求函数解析式的基本步骤吗?
象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
师:一次函数的图象直线--满足条件的两定点--函数解析式y=kx+b---》从形到数的过程.
数学的基本思想方法:数形结合
三、巩固拓展知识升华
教师多媒体出示:
1.利用点的坐标求函数解析式
已知一条直线与x轴交点的横坐标为-1,与y轴交点的纵坐标为-3,求这条直线的解析式.
请同学们根据这个图象特征写出这条直线所代表的一次函数的解析式.
学生讨论.
教师提示:由图象我们能看出图象经过了哪两个点?
生:(-1,0)和(0,-3)这两点.
教师找一名学生板演,其余学生在下面做,然后集体订正.
?
解:设这条直线解析式为:y=kx+b,由题意知,其图像过(-1,0),(0,-3)得方程组
-k+b=0
b=-3
?
解得K=-3
b=-3
?
这条直线解析式为:y=-3x-3
2.利用表格信息确定函数解析式
小明根据某个一次函数关系式填写了下表:
x
-2
-1
0
1
y
3
?
1
0
其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?
?
解:设这条直线解析式为:y=kx+b,由题意知,其图像过(0,1),(1,0)得方程组b=1
k+b=0
解得:k=-1
b=1
?
这条直线解析式为:y=-x+1
?
所以当x=-1时y=-1
(-1)+1=2
?
即墨迹下应是2
3.利用已知的规律等求函数解析式
已知一条直线于直线y=2x平行,且与y轴交点的纵坐标为
-
-3,则其解析式为_________
师:平行直线解析式有何特征?什么叫截距?
生:k相同的直线互相平行;直线与y轴相交时交点的纵坐标读数叫截距.
四、反思总结
师:
确定正比例函数的解析式y=kx,需求哪个值?需要几个条件?
确定一次函数的解析式y=kx+b,需求哪个值?需要几个条件?
学生回答,教师补充完善.
总结:在确定函数解析式时,要求几个系数就需要知道几个条件。
求函数解析式的一般步骤是怎样的呢?
可归纳为:“一设、二列、三解、四还原”
(一)设:设出函数关系式的一般形式y=kx+b
(二)列:根据已知两点的坐标列出关于k、b的二元
一次方程组;
(三)解:解这个方程组,求出k、b的值;
(四)还原:把求得的k、b的值代入y=kx+b,写出函
数关系式.
五
求一次函数关系式常见题型:
1.利用图像求函数关系式
2.利用点的坐标求函数关系式
六
课外选作
1.若一次函数的图象经过点
A(2,0)且与直线y=-x+3平行,求其解析式
2.若一次函数的图象与直线y=-3x+2交y轴于同一点,且过点(2,-6),求此函数解析式
七,课外作业:课本p40练习1,2,
?
P47-48习题12.2
第9,10题
图1
图2
