冀教版初中数学八年级上册 第十二章 分式方程复习 课件(共23张ppt)
文档属性
| 名称 | 冀教版初中数学八年级上册 第十二章 分式方程复习 课件(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 696.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览






文档简介
分式方程复习课
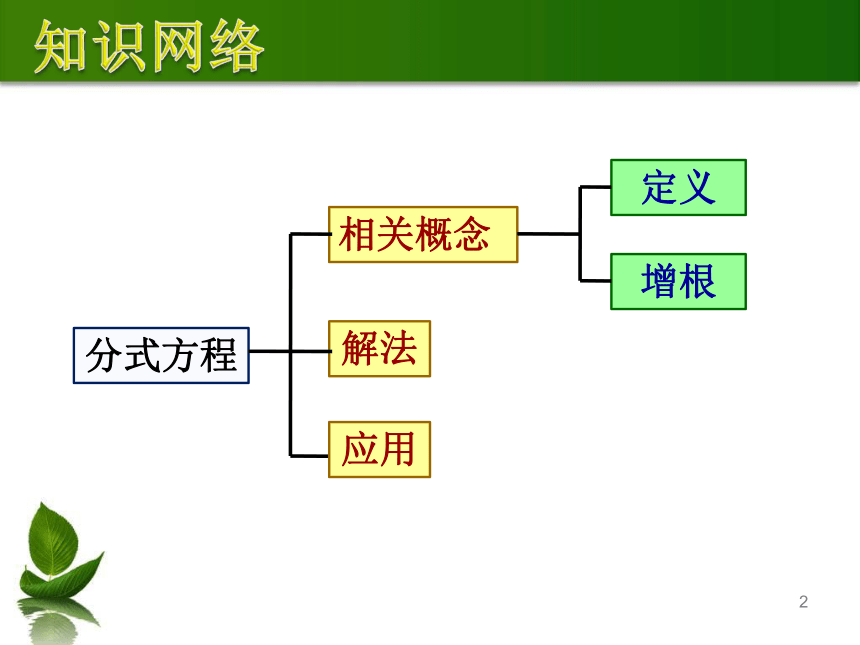
分式方程
相关概念
解法
定义
增根
应用
学习目标
1、通过对例1的解答复习分式方程的概念,会识别分式方程,并体会分式方程的重要特征;
2、通过解分式方程的训练,进一步掌握解分式方程的一般步骤,体会转化的数学思想;
3、通过列分式方程解决实际问题,经历“实际问题-建立分式方程模型-求解-解释解的合理性”的过程,体会数学建模的思想.
任务1:把例1的答案输到选择器中,并准备回答其它选项中不是分式方程的原因;
方式:老师喊“开始”后输入答案,
并叫 号回答原因;
检测与评价:大胆点评、合理补充、质疑的加2分,要求大胆、大声、大方.
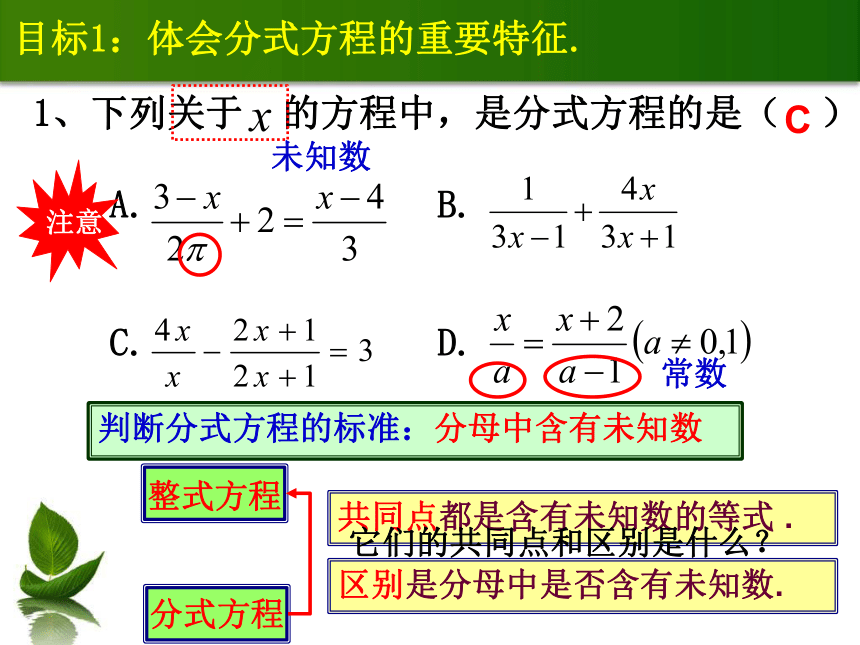
目标1:体会分式方程的重要特征.
1、下列关于 的方程中,是分式方程的是( )
A. B.
C. D.
C
目标1:体会分式方程的重要特征.
分式方程
整式方程
区别是分母中是否含有未知数.
共同点都是含有未知数的等式 .
判断分式方程的标准:分母中含有未知数
注意
未知数
常数
它们的共同点和区别是什么?
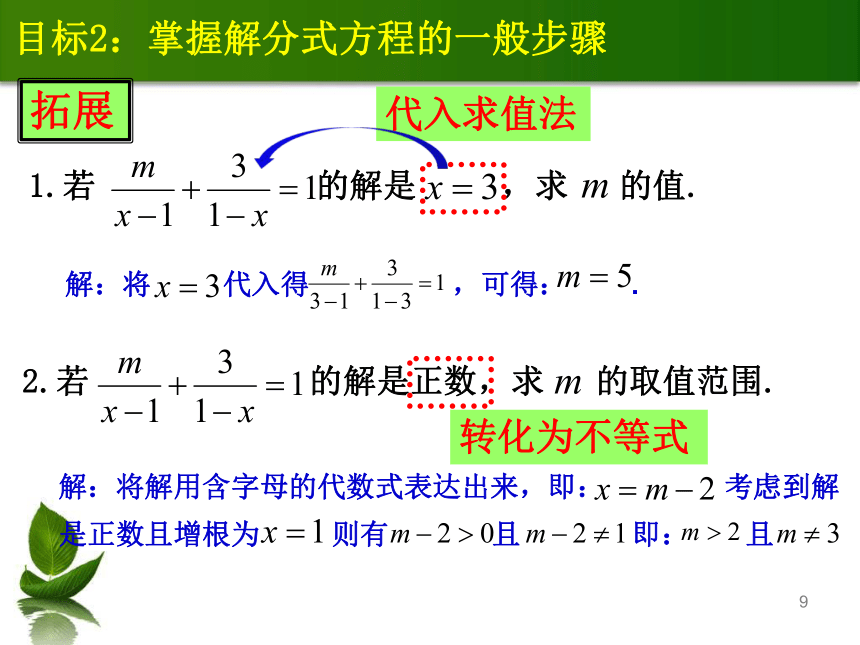
目标2:掌握解分式方程的一般步骤
任务2:小组派代表展示,奇数小组板演(1),偶数小组板演(2),要求书写整齐清楚;
时间:5分钟;
方式:每组 5 号板演,其余学生组内对子互评,组长统计全对人数;
检测与评价:每组 2 号上黑板点评,板演整齐、正确加2分,点评合理准确加1分,其他同学补充、质疑加1分.
2
去分母
去括号
移项
合并同类项
系数化为1
分式方程
整式方程
去分母
转化
解整式方程
①
②
③
检验
常数项别漏乘
最简公分母
目标2:掌握解分式方程的一般步骤
解:
解:方程两边同乘 得:
检验:当 时, .
所以: 是原分式方程的增根,
原分式方程无解。
2(2)
目标2:掌握解分式方程的一般步骤
1.若 的解是 ,求 的值.
拓展
2.若 的解是正数,求 的取值范围.
解:将 代入得 ,可得: .
解:将解用含字母的代数式表达出来,即: 考虑到解是正数且增根为 则有 且 即: 且
代入求值法
转化为不等式
目标2:掌握解分式方程的一般步骤
解:整理方程得:
∵分式方程无解.
?分式方程存在增根
即
3.若 有增根,
求 的值.
解:方程整理得即: 考虑到方程有根增时 ,则 ,即: .
目标2:掌握解分式方程的一般步骤
变式.若 无解,
求 的取值范围.
?化简后的整式方程无解.
即
分式方程
整式方程
转化
去分母
无解
增根
未知数的系数为0
目标3:列分式方程解决实际问题
任务3:通过投影展示例4的做法
(注意只讲解思路、做法,不讲过程);
时间:5分钟;
方式:举手回答;
检测与评价:表述清晰、思路正确的加2分,合理补充、点评、质疑的加1分,要求大胆、大声、大方.
4、某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家由用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1) 该商家购进的第一批衬衫是多少件?
目标3:列分式方程解决实际问题
(2) 若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
4、某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家由用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1) 该商家购进的第一批衬衫是多少件?
目标3:列分式方程解决实际问题
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
-
设未知数
列分式方程
3、某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家由用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1) 该商家购进的第一批衬衫是多少件?
目标3:列分式方程解决实际问题
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
设未知数
列分式方程
=
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
-
设未知数
列分式方程
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
设未知数
列分式方程
=
目标3:列分式方程解决实际问题
解:设商家购进第一批衬衫的数量为x件,则第二批衬衫的数量为2x件.
解得:
经检验: 为原分式方程的解.
答:商家购进第一批衬衫的数量为120件.
解:设商家购进第一批衬衫的单价为x元,则第二批衬衫的单价为x+10元.
经检验: 为原分式方程的解.
答:商家购进第一批衬衫的数量为120件.
解得:
目标3:列分式方程解决实际问题
直接设法
间接设法
列分式方程解应用题的一般步骤
1.审:分析题意,找出关键句,建立等量关系.
2.设:选择恰当的未知数,注意单位.
3.列:根据等量关系正确列出方程.
4.解:规范格式.
5.验:不要忘记检验.
6.答:不要忘记写.
学习目标回头看
1、通过对例1的解答复习分式方程的概念,会识别分式方程,并体会分式方程的重要特征;
2、通过解分式方程的训练,进一步掌握解分式方程的一般步骤,体会转化的数学思想;
3、通过列分式方程解决实际问题,经历“实际问题-建立分式方程模型-求解-解释解的合理性”的过程,体会数学建模的思想.
分式方程
相关概念
解法
定义
增根
应用
1、下列关于 的方程中,是分式方程的是( )
A. B.
C. D.
C
目标1:体会分式方程的重要特征.
分式方程
整式方程
区别是分母中是否含有未知数.
共同点都是含有未知数的等式 .
判断分式方程的标准:分母中含有未知数
注意
未知数
常数
去分母
去括号
移项
合并同类项
系数化为1
分式方程
整式方程
去分母
转化
解整式方程
①
②
③
检验
常数项别漏乘
最简公分母
目标2:掌握解分式方程的一般步骤
列分式方程解应用题的一般步骤
1.审:分析题意,找出研究对象.
3.设:选择恰当的未知数,注意单位.
4.列:根据等量关系正确列出方程.
5.解:认真仔细.
6.验:不要忘记检验.
7.答:不要忘记写.
2.找:找出关键句,建立等量关系.
分式的基本性质
分式的乘除
分式的加减
分式方程
分式和分式方程
分式
分式的运算
通分
约分
概念
解法
应用
THANKS
分式方程
相关概念
解法
定义
增根
应用
学习目标
1、通过对例1的解答复习分式方程的概念,会识别分式方程,并体会分式方程的重要特征;
2、通过解分式方程的训练,进一步掌握解分式方程的一般步骤,体会转化的数学思想;
3、通过列分式方程解决实际问题,经历“实际问题-建立分式方程模型-求解-解释解的合理性”的过程,体会数学建模的思想.
任务1:把例1的答案输到选择器中,并准备回答其它选项中不是分式方程的原因;
方式:老师喊“开始”后输入答案,
并叫 号回答原因;
检测与评价:大胆点评、合理补充、质疑的加2分,要求大胆、大声、大方.
目标1:体会分式方程的重要特征.
1、下列关于 的方程中,是分式方程的是( )
A. B.
C. D.
C
目标1:体会分式方程的重要特征.
分式方程
整式方程
区别是分母中是否含有未知数.
共同点都是含有未知数的等式 .
判断分式方程的标准:分母中含有未知数
注意
未知数
常数
它们的共同点和区别是什么?
目标2:掌握解分式方程的一般步骤
任务2:小组派代表展示,奇数小组板演(1),偶数小组板演(2),要求书写整齐清楚;
时间:5分钟;
方式:每组 5 号板演,其余学生组内对子互评,组长统计全对人数;
检测与评价:每组 2 号上黑板点评,板演整齐、正确加2分,点评合理准确加1分,其他同学补充、质疑加1分.
2
去分母
去括号
移项
合并同类项
系数化为1
分式方程
整式方程
去分母
转化
解整式方程
①
②
③
检验
常数项别漏乘
最简公分母
目标2:掌握解分式方程的一般步骤
解:
解:方程两边同乘 得:
检验:当 时, .
所以: 是原分式方程的增根,
原分式方程无解。
2(2)
目标2:掌握解分式方程的一般步骤
1.若 的解是 ,求 的值.
拓展
2.若 的解是正数,求 的取值范围.
解:将 代入得 ,可得: .
解:将解用含字母的代数式表达出来,即: 考虑到解是正数且增根为 则有 且 即: 且
代入求值法
转化为不等式
目标2:掌握解分式方程的一般步骤
解:整理方程得:
∵分式方程无解.
?分式方程存在增根
即
3.若 有增根,
求 的值.
解:方程整理得即: 考虑到方程有根增时 ,则 ,即: .
目标2:掌握解分式方程的一般步骤
变式.若 无解,
求 的取值范围.
?化简后的整式方程无解.
即
分式方程
整式方程
转化
去分母
无解
增根
未知数的系数为0
目标3:列分式方程解决实际问题
任务3:通过投影展示例4的做法
(注意只讲解思路、做法,不讲过程);
时间:5分钟;
方式:举手回答;
检测与评价:表述清晰、思路正确的加2分,合理补充、点评、质疑的加1分,要求大胆、大声、大方.
4、某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家由用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1) 该商家购进的第一批衬衫是多少件?
目标3:列分式方程解决实际问题
(2) 若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
4、某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家由用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1) 该商家购进的第一批衬衫是多少件?
目标3:列分式方程解决实际问题
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
-
设未知数
列分式方程
3、某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家由用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1) 该商家购进的第一批衬衫是多少件?
目标3:列分式方程解决实际问题
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
设未知数
列分式方程
=
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
-
设未知数
列分式方程
第一批衬衫的数量
第二批衬衫的数量
=
2×
第二批衬衫的单价-第一批衬衫的单价=10
设未知数
列分式方程
=
目标3:列分式方程解决实际问题
解:设商家购进第一批衬衫的数量为x件,则第二批衬衫的数量为2x件.
解得:
经检验: 为原分式方程的解.
答:商家购进第一批衬衫的数量为120件.
解:设商家购进第一批衬衫的单价为x元,则第二批衬衫的单价为x+10元.
经检验: 为原分式方程的解.
答:商家购进第一批衬衫的数量为120件.
解得:
目标3:列分式方程解决实际问题
直接设法
间接设法
列分式方程解应用题的一般步骤
1.审:分析题意,找出关键句,建立等量关系.
2.设:选择恰当的未知数,注意单位.
3.列:根据等量关系正确列出方程.
4.解:规范格式.
5.验:不要忘记检验.
6.答:不要忘记写.
学习目标回头看
1、通过对例1的解答复习分式方程的概念,会识别分式方程,并体会分式方程的重要特征;
2、通过解分式方程的训练,进一步掌握解分式方程的一般步骤,体会转化的数学思想;
3、通过列分式方程解决实际问题,经历“实际问题-建立分式方程模型-求解-解释解的合理性”的过程,体会数学建模的思想.
分式方程
相关概念
解法
定义
增根
应用
1、下列关于 的方程中,是分式方程的是( )
A. B.
C. D.
C
目标1:体会分式方程的重要特征.
分式方程
整式方程
区别是分母中是否含有未知数.
共同点都是含有未知数的等式 .
判断分式方程的标准:分母中含有未知数
注意
未知数
常数
去分母
去括号
移项
合并同类项
系数化为1
分式方程
整式方程
去分母
转化
解整式方程
①
②
③
检验
常数项别漏乘
最简公分母
目标2:掌握解分式方程的一般步骤
列分式方程解应用题的一般步骤
1.审:分析题意,找出研究对象.
3.设:选择恰当的未知数,注意单位.
4.列:根据等量关系正确列出方程.
5.解:认真仔细.
6.验:不要忘记检验.
7.答:不要忘记写.
2.找:找出关键句,建立等量关系.
分式的基本性质
分式的乘除
分式的加减
分式方程
分式和分式方程
分式
分式的运算
通分
约分
概念
解法
应用
THANKS
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
