冀教版初中数学九年级上册 28.2 过三点的圆 课件(共17张ppt)
文档属性
| 名称 | 冀教版初中数学九年级上册 28.2 过三点的圆 课件(共17张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 721.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 22:13:13 | ||
图片预览



文档简介
28.2 过三点的圆
第二十八章 圆
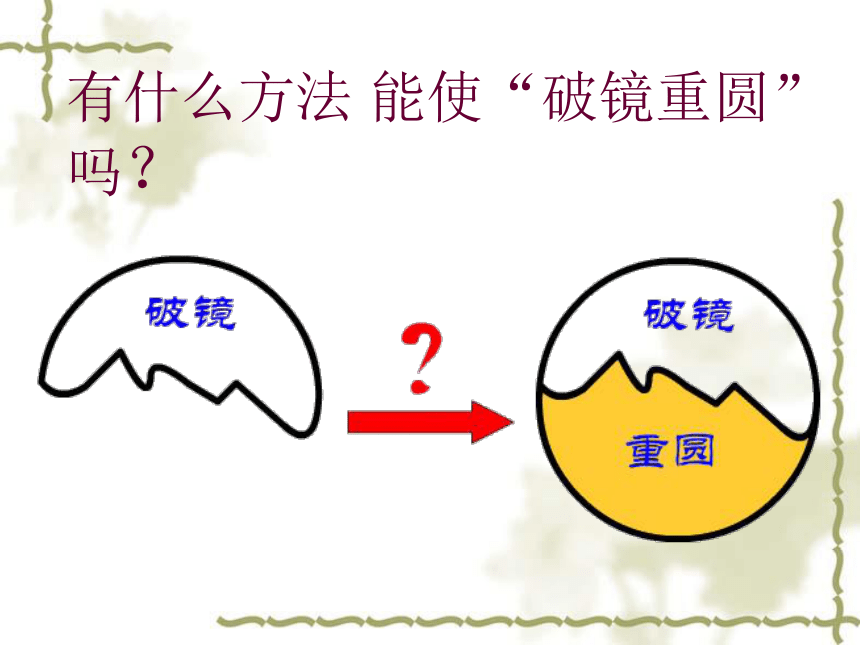
有什么方法 能使“破镜重圆”吗?
1.复习并巩固圆中的基本概念.
2.理解并掌握三点确定圆的条件并会应用. (重点)
3.理解并掌握三角形的外接圆及外心的概念.(难点)
学习目标
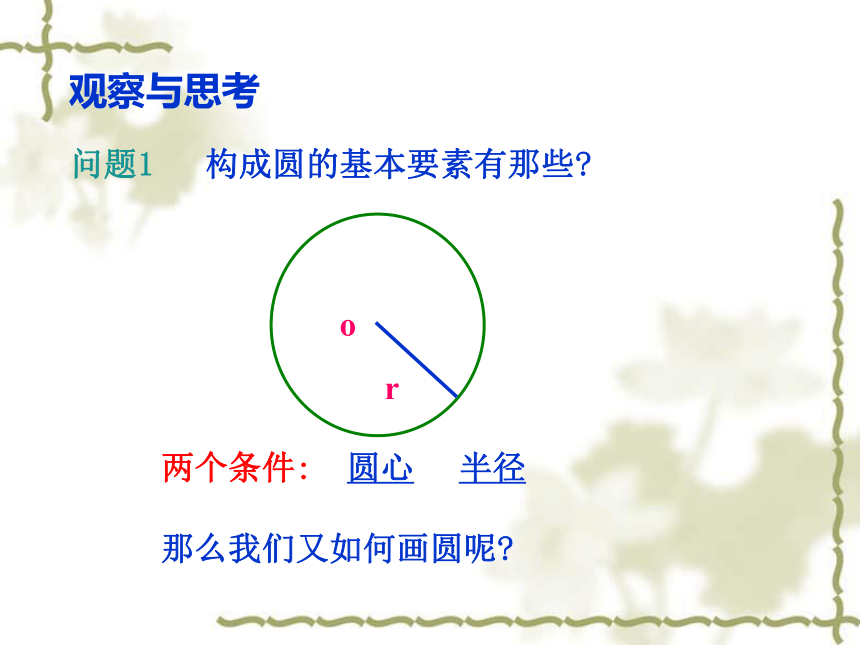
问题1 构成圆的基本要素有那些?
观察与思考
两个条件:
圆心
半径
那么我们又如何画圆呢?
o
r
问题2 过一点可以作几条直线?
问题3 过几点可以确定一条直线?那么过几点可以确定一个圆呢?
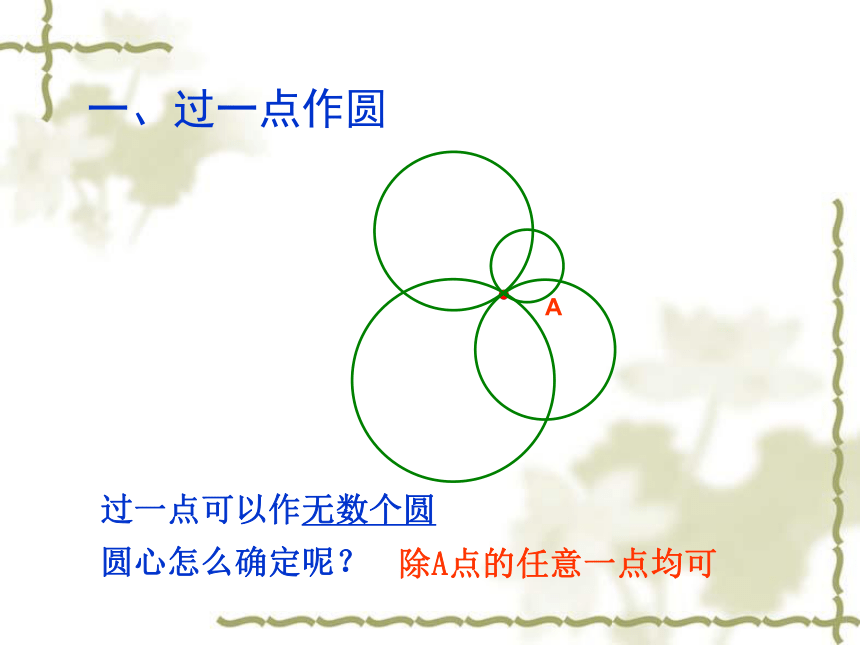
一、过一点作圆
过一点可以作无数个圆
A
圆心怎么确定呢?
除A点的任意一点均可
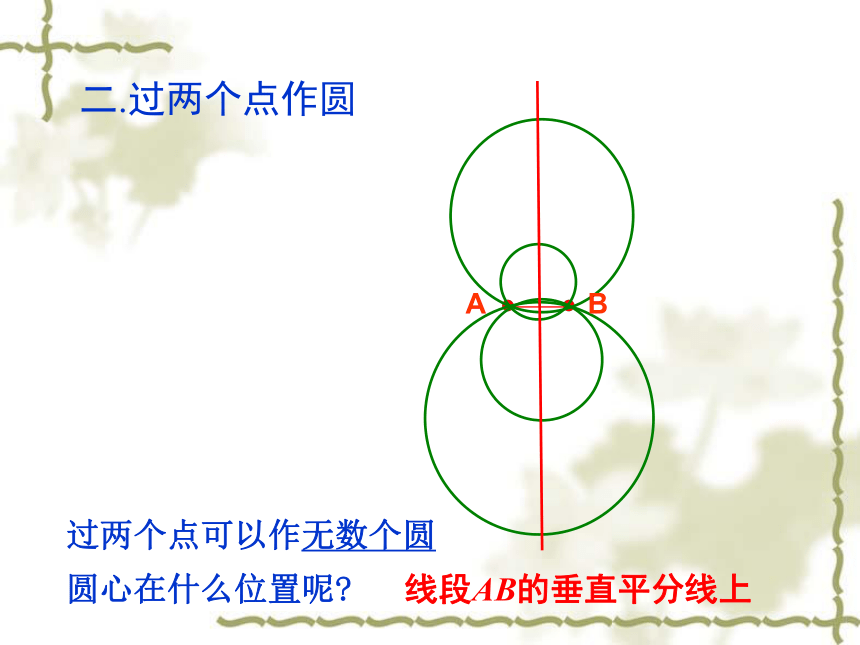
二.过两个点作圆
过两个点可以作无数个圆
圆心在什么位置呢?
线段AB的垂直平分线上
A
B
A
B
C
已知:不在同一直线上的三点A、B、C
求作:⊙O,使它经过A、B、C
1、连结AB,作线段AB的垂直平分线ED
O
D
E
G
F
2、连结BC,作线段BC的垂直平分线FG,交DE于点O
3、以O为圆心,OA为半径作圆,
作法:
⊙O就是所求作的圆
归纳
A
B
C
过如下三点能不能做圆? 为什么?
不在同一直线上的三点确定一个圆.
问题1:经过三个点A、B、C一定能确定一个圆吗?
不能,三点在同一直线上.
头脑风暴
问题2 已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
头脑风暴
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
三角形的外心到三角形的三个顶点的距离相等.
归纳
O
O
C
B
A
C
B
A
O
C
B
A
锐角三角形的外心在三角形内部。
直角三角形的外心在斜边的中点处。
钝角三角形的外心在三角形外部。
1、判断:
(1)过两点可以作无数个圆( )
(2)顶点都在圆上的三角形叫作圆的外接三角形( )
(3)三角形的外心到三边的距离都相等( )
(4)三角形三个顶点不一定共圆( )
(5)一个三角形只有一个外接圆,一个圆也只有一个内接三角形( )
2、填空:
已知直角三角形的两条直角边长为5cm和12cm,这个三角形的外接圆半径是 。
当堂练
3、解答题
(1)如图,在四点A、B、C、D中,任意三点都不在统一直线上.作过A、B、C三点的圆,并判断这个圆是否过点D.
·
·
·
·
B
A
C
D
3、解答题
(2)如图,已知∠APB和点Q.过点PQ,且圆心在∠APB的边上的圆有几个?请将它们画出来。
·
A
P
B
Q
课堂小结
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定;
(2)经过一个已知点能作无数个圆;
(3)经过两个已知点A、B能作无数个圆,这些圆的圆心在线段AB的垂直平分线上;
(4)不在同一直线上的三个点确定一个圆;
(5)经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;这个三角形叫做圆的内接三角形.
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
第二十八章 圆
有什么方法 能使“破镜重圆”吗?
1.复习并巩固圆中的基本概念.
2.理解并掌握三点确定圆的条件并会应用. (重点)
3.理解并掌握三角形的外接圆及外心的概念.(难点)
学习目标
问题1 构成圆的基本要素有那些?
观察与思考
两个条件:
圆心
半径
那么我们又如何画圆呢?
o
r
问题2 过一点可以作几条直线?
问题3 过几点可以确定一条直线?那么过几点可以确定一个圆呢?
一、过一点作圆
过一点可以作无数个圆
A
圆心怎么确定呢?
除A点的任意一点均可
二.过两个点作圆
过两个点可以作无数个圆
圆心在什么位置呢?
线段AB的垂直平分线上
A
B
A
B
C
已知:不在同一直线上的三点A、B、C
求作:⊙O,使它经过A、B、C
1、连结AB,作线段AB的垂直平分线ED
O
D
E
G
F
2、连结BC,作线段BC的垂直平分线FG,交DE于点O
3、以O为圆心,OA为半径作圆,
作法:
⊙O就是所求作的圆
归纳
A
B
C
过如下三点能不能做圆? 为什么?
不在同一直线上的三点确定一个圆.
问题1:经过三个点A、B、C一定能确定一个圆吗?
不能,三点在同一直线上.
头脑风暴
问题2 已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
头脑风暴
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
三角形的外心到三角形的三个顶点的距离相等.
归纳
O
O
C
B
A
C
B
A
O
C
B
A
锐角三角形的外心在三角形内部。
直角三角形的外心在斜边的中点处。
钝角三角形的外心在三角形外部。
1、判断:
(1)过两点可以作无数个圆( )
(2)顶点都在圆上的三角形叫作圆的外接三角形( )
(3)三角形的外心到三边的距离都相等( )
(4)三角形三个顶点不一定共圆( )
(5)一个三角形只有一个外接圆,一个圆也只有一个内接三角形( )
2、填空:
已知直角三角形的两条直角边长为5cm和12cm,这个三角形的外接圆半径是 。
当堂练
3、解答题
(1)如图,在四点A、B、C、D中,任意三点都不在统一直线上.作过A、B、C三点的圆,并判断这个圆是否过点D.
·
·
·
·
B
A
C
D
3、解答题
(2)如图,已知∠APB和点Q.过点PQ,且圆心在∠APB的边上的圆有几个?请将它们画出来。
·
A
P
B
Q
课堂小结
(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定;
(2)经过一个已知点能作无数个圆;
(3)经过两个已知点A、B能作无数个圆,这些圆的圆心在线段AB的垂直平分线上;
(4)不在同一直线上的三个点确定一个圆;
(5)经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;这个三角形叫做圆的内接三角形.
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
