冀教版初中数学九上 26.4 解直角三角形的应用 课件(共21张ppt)
文档属性
| 名称 | 冀教版初中数学九上 26.4 解直角三角形的应用 课件(共21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 279.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 15:58:35 | ||
图片预览





文档简介
解直角三角形习题课
三边之间的关系
a2+b2=c2(勾股定理)
锐角之间的关系
∠A+∠B=90°
边角之间的关系(锐角三角函数)
tanA=
a
b
sinA =
a
c
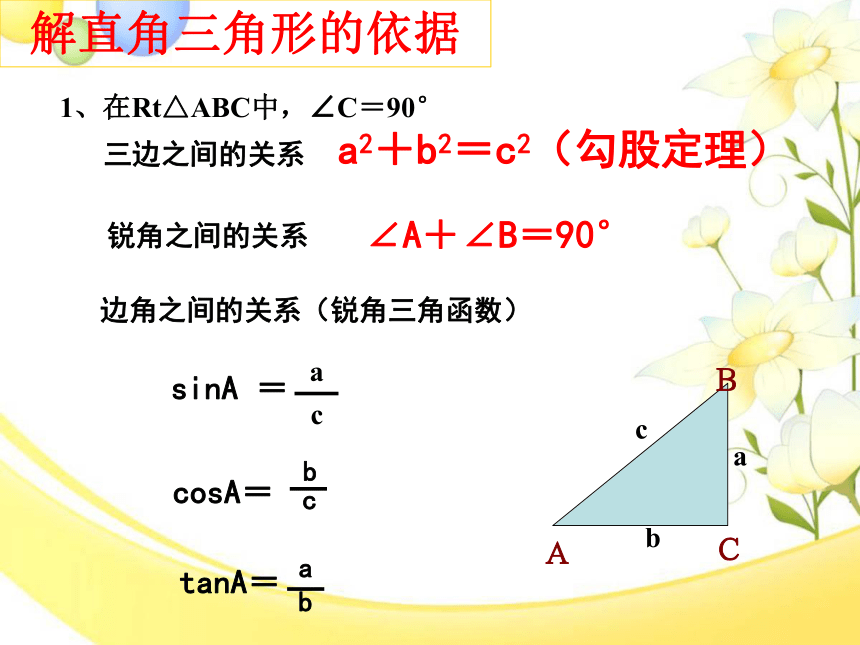
1、在Rt△ABC中,∠C=90°
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
知一边一锐角解直角三角形
知两边解直角三角形
解直角三角形
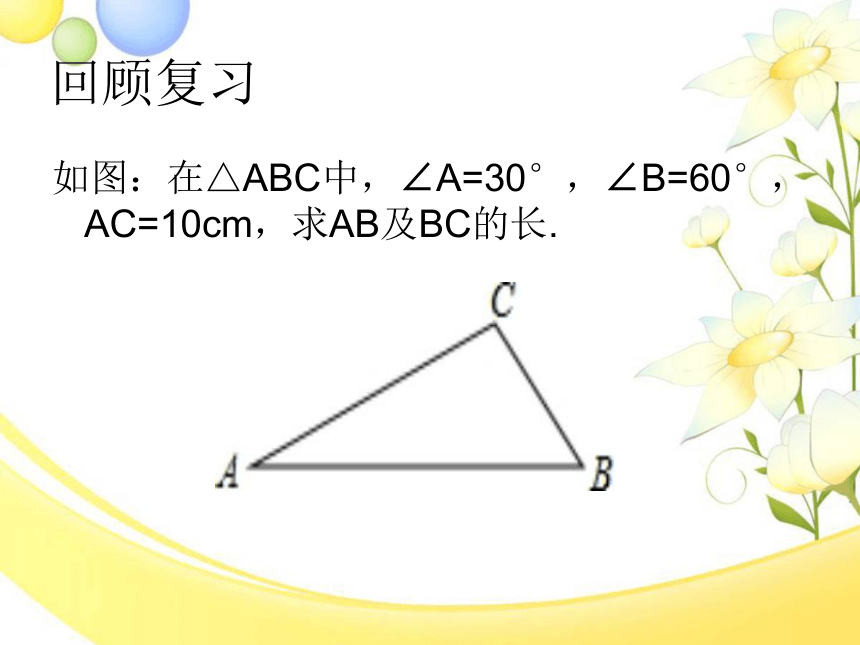
回顾复习
如图:在△ABC中,∠A=30°,∠B=60°,AC=10cm,求AB及BC的长.
提出问题:
非直角三角形:应如何解决?.
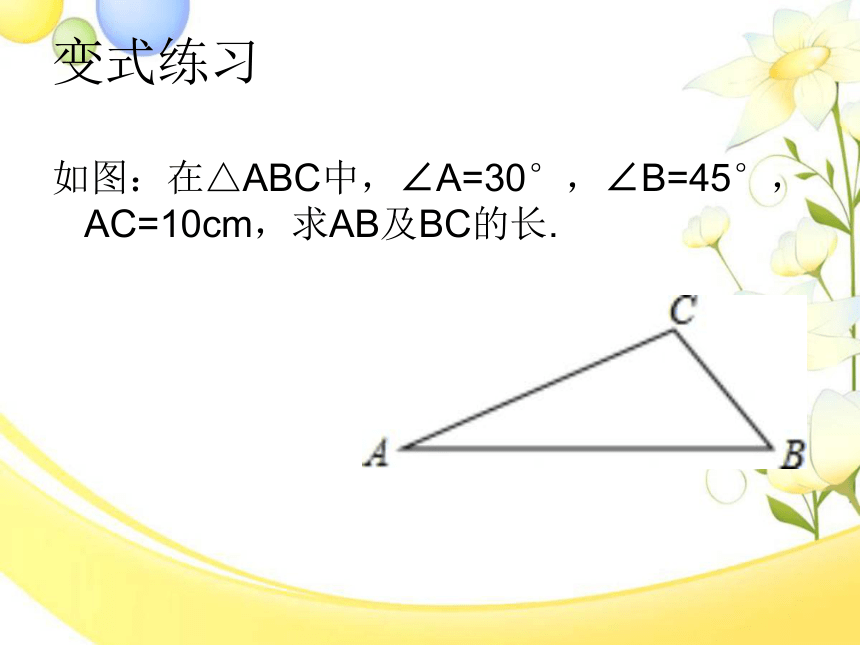
变式练习
如图:在△ABC中,∠A=30°,∠B=45°,AC=10cm,求AB及BC的长.
问题探究
探究1.边长不变,角度由30 °、45 °、
改为一般角
探究2.角度不变,已知边长改变
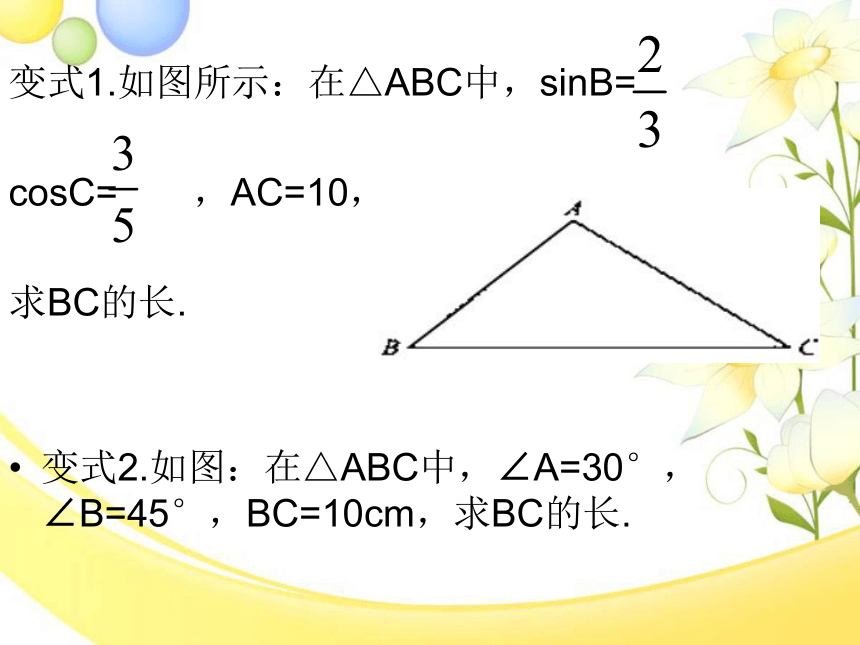
变式1.如图所示:在△ABC中,sinB=
cosC= ,AC=10,
求BC的长.
?
?
变式2.如图:在△ABC中,∠A=30°,∠B=45°,BC=10cm,求BC的长.
?
如果高线在三角形的外部,已知条件应做怎样变化?
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线(作高线),将其转换为直角三角形来解.
提示
D
题中给出的边是直角三角形的边:
如图:在Rt△ABC中, ∠A=30 °, ∠BDC=45 °,BD=4,求AB的长.
在上题中,若AD=4,其它条件不变,求BC的长.
题中给出的边是不是直角三角形的边:
在上题中,如果∠BDC=60 °,AD=4,其它条件不变,求AB的长.
巩固练习:
1.如图:在△ABC中, ∠B=30 °,∠BAC=105 °,AB=24,
求BC 的长.
2. 如图,在Rt△ABC中,∠ACB =90°,CD⊥AB于点D,已知AC=
BC=2,那么sin∠ACD=( )
,
A.
A
A
B
C
3.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.
D
A
B
C
D
E
4.已知在RT△ABC中,∠C=900,D是BC中
点,DE⊥AB,垂足为E,sin∠BDE=
AE=7,求DE的长.
某兴趣小组借助无人机航拍校园,如图:无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
为维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图:正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
如图,某军港有一雷达站P,军舰M停泊在雷达站P的南偏东60°方向36海里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距 海里.求:
(1)军舰N在雷达站P的什么方向;
(2)两军舰M,N的距离.(结果保留根号)
三边之间的关系
a2+b2=c2(勾股定理)
锐角之间的关系
∠A+∠B=90°
边角之间的关系(锐角三角函数)
tanA=
a
b
sinA =
a
c
1、在Rt△ABC中,∠C=90°
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
知一边一锐角解直角三角形
知两边解直角三角形
解直角三角形
回顾复习
如图:在△ABC中,∠A=30°,∠B=60°,AC=10cm,求AB及BC的长.
提出问题:
非直角三角形:应如何解决?.
变式练习
如图:在△ABC中,∠A=30°,∠B=45°,AC=10cm,求AB及BC的长.
问题探究
探究1.边长不变,角度由30 °、45 °、
改为一般角
探究2.角度不变,已知边长改变
变式1.如图所示:在△ABC中,sinB=
cosC= ,AC=10,
求BC的长.
?
?
变式2.如图:在△ABC中,∠A=30°,∠B=45°,BC=10cm,求BC的长.
?
如果高线在三角形的外部,已知条件应做怎样变化?
C
A
B
D
A
B
C
E
求解非直角三角形的边角问题,常通过添加适当的辅助线(作高线),将其转换为直角三角形来解.
提示
D
题中给出的边是直角三角形的边:
如图:在Rt△ABC中, ∠A=30 °, ∠BDC=45 °,BD=4,求AB的长.
在上题中,若AD=4,其它条件不变,求BC的长.
题中给出的边是不是直角三角形的边:
在上题中,如果∠BDC=60 °,AD=4,其它条件不变,求AB的长.
巩固练习:
1.如图:在△ABC中, ∠B=30 °,∠BAC=105 °,AB=24,
求BC 的长.
2. 如图,在Rt△ABC中,∠ACB =90°,CD⊥AB于点D,已知AC=
BC=2,那么sin∠ACD=( )
,
A.
A
A
B
C
3.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.
D
A
B
C
D
E
4.已知在RT△ABC中,∠C=900,D是BC中
点,DE⊥AB,垂足为E,sin∠BDE=
AE=7,求DE的长.
某兴趣小组借助无人机航拍校园,如图:无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
为维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图:正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
如图,某军港有一雷达站P,军舰M停泊在雷达站P的南偏东60°方向36海里处,另一艘军舰N位于军舰M的正西方向,与雷达站P相距 海里.求:
(1)军舰N在雷达站P的什么方向;
(2)两军舰M,N的距离.(结果保留根号)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
