人教版九年级数学25.1 随机事件与概率(共36张ppt)
文档属性
| 名称 | 人教版九年级数学25.1 随机事件与概率(共36张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览











文档简介
25.1 随机事件与概率
新人教版九年级数学上册 25 概率初步
理解必然事件、不可能事件、随机事件的概念,能判断一件事情属于哪类事件;
在具体情境中了解概率的意义,计算一些简单随机事件的概率。
学习目标
天有不测风云
刮风
下雨
闪电
天晴
不看不知道,世界真奇妙
!
天有不测风云
思考:下列哪些现象是必然发生的,
哪些现象是不可能发生的?
太阳东升西落!
测量某天气温,结果为
-150°C!
今年是2018年!
两个正实数相加,
结果为负!
(不可能发生)
(必然发生)
(必然发生)
(不可能发生)
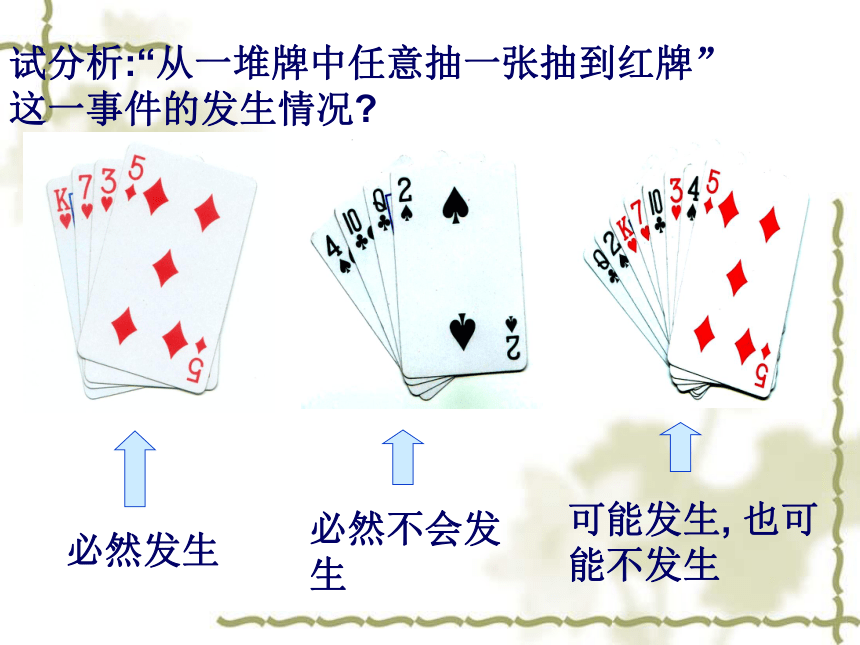
试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?
可能发生, 也可能不发生
必然发生
必然不会发生
小明从盒中任意摸出一球,
一定能摸到红球吗?
小麦从盒中摸出的球一定是白球吗?
小米从盒中摸出的球一定是红球吗?
三人每次都能摸到红球吗?
在自然界和实际生活中,我们会遇到各种各样的现象.
如果从结果能否预知的角度来看,可以分为两大类:
另一类现象的结果是无法预知的,即在一定的条件下,出现那种结果是无法预先确定的,这类现象称为随机现象.
一类现象的结果总是确定的,即在一定的条件下,它所出现的结果是可以预知的,这类现象称为确定性现象;
在一定条件下:
必然会发生的事件叫做必然事件;
必然不会发生的事件或者不可能发生的事件叫做不可能事件;
可能会发生,也可能不发生的事件叫做不确定事件或随机事件.
特征:事先不能预料即具有不确定性。
1.将一小勺白糖放入一杯温水中,并用筷子不断的搅拌,白糖溶解.
2.测量某天的最低气温,结果为—350℃.
3.小强打开电视机,电视里正在播放广告.
4.互为相反数的两个数的和等于0.
5.下过一场雨后,天空上出现一条彩虹.
不可能事件
必然事件
随机事件
判断下列事件中哪些是必然事件,哪些是不可能事件,哪些是随机事件.
例 题
必然事件
随机事件
1、在地球上,太阳每天从东方升起.
2、有一匹马奔跑的速度是70千米/秒.
3、明天,我买一注体育彩票,得500万大奖.
判断下列事件中哪些是必然事件,哪些是不可能事件,哪些是随机事件?
4、用长为3cm、4cm、7cm的三条线段首尾顺次连结,构成一个三角形.
5、掷一枚均匀的硬币,正面朝上.
跟踪训练
必然事件
不可能事件
随机事件
不可能事件
随机事件
8、人在月球上所受的重力比地球上小.
9、明年我市十·一的最高气温是三十摄氏度.
7、在标准大气压下,温度在0摄氏度以下,纯净水会结成冰.
6、2018年12月12日当天我市下雨.
随机事件
必然事件
随机事件
必然事件
1.下列事件是随机事件的是( )
A.人长生不老.
B.2018年世界杯巴西队必夺冠.
C.一个星期为七天.
D. 掷两枚质地均匀的正方体骰子朝上一面的点数之
积为36.
D
【解析】
2.(杭州·中考)“a是实数,则 ”这一事件是
A. 必然事件 B. 不确定事件
C. 不可能事件 D. 随机事件
3.(晋江·中考)下列事件中,是确定事件的是( )
A.打雷后会下雨 B.明天是睛天
C.1小时等于60分钟 D.下雨后有彩虹
【解析】选C.ABD都是不确定事件,C是确定事件.
选A.a是实数, 则 ,是必然事件.
课堂小结
4、一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小可能不同。
1、在一定条件下必然要发生的事件叫必 然事件.
2、在一定条件下不可能发生的事件叫不可能事件.
3、在一定条件下可能发生也可能不发生的事件叫随机事件.
可能的结果有1,2,3,4,5等5种,由于纸签的形状,大小相同,又是随机抽取的,所以我们可以认为:每个号被抽到的可能性相等,都是
试验1.从分别标有1.2.3.4.5号的5根纸签中随机抽取一根,抽出的签上的标号有几种可能?每一种抽取的可能性大小相等么?
试验2.抛掷一个骰子,它落地时向上的数有几种可能?分别是什么?发生的可能性大小一样吗?是多少?
6种等可能的结果:1,2,3,4,5,6.由于骰子的构造相同,质地均匀,又是随机掷出的,所以,每种结果的可能性相等,
都是
归纳
一般地,对于一个随机事件A,把刻画其发生可能性大小的数值,称之为随机事件A发生的概率。记为P(A)
共同特征: 1.每一次试验中,可能出现的结果只有有限个。2. 每一次试验中,各种结果出现的可能性相等。
概率从数量上刻画了一个随机事件发生的可能性的大小。
具有这些特点的试验称为古典概率.在这些试验中出现的事件为等可能事件.
例如,在上面抽签试验中,“抽到1号”这个事件包含____种可能结果,在全部___种可能的结果中所占的比为
______,于是这个事件的概率为
___ ___
1
5
“抽到偶数号”这个事件包含抽到( )和( )这( )种可能结果,在全部5种可能结果中所占的比为( ),于是这个事件的概率
2
4
2
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率 .
等可能事件概率的求法
1、当A是必然发生的事件时,P(A)是多少 ?
2、当A是不可能发生的事件时,P(A)是多少?
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
不可能事件,必然事件与随机事件的关系
想一想
必然事件发生的可能性是
100%
,P(A)=1;
不可能事件发生的可能性是
0;
P(A)= 0;
3、不确定事件发生的可能性是大于0而小于1的.
即随机事件的概率为
由定义可知:
(1)概率反映了随机事件发生的可能性的大小。事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0;
(2)必然事件的概率为1,不可能事件的概率为0.因此 .
(3)随机事件的概率为
例1.掷一枚骰子,观察向上的一面的点数,求下列事件的概率。
①点数为2.
P(点数为2)=
②点数为奇数。
P(点数为奇数)=
③点数大于2且小于5.
P(点数大于2且小于5)=
例1变式 掷1个质地均匀的正方体骰子,观察向上一面的点数,
(1)求掷得点数为2或4或6的概率;
(2)小明在做掷骰子的试验时,前五次都没掷得点数2,求他第六次掷得点数2的概率。
例2.如图:是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率。
(1)P(指向红色)=_____
(2)P(指向红色或黄色)=_______
(3)P(不指向红色)= ________
1.明天下雨的概率为95%,那么
下列说法错误的是( )
(A) 明天下雨的可能性较大
(B) 明天不下雨的可能性较小
(C) 明天有可能是晴天
(D) 明天不可能是晴天
练习:
D
2、1袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则
P(摸到红球)= ;
P(摸到白球)= ;
P(摸到黄球)= 。
1
-
9
1
-
3
5
-
9
3、有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则:
p (摸到1号卡片)= ;
p (摸到2号卡片)= ;
p (摸到奇数号卡片)= ;
P(摸到偶数号卡片) = .
4、设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只,则从中任意取1只,是二等品的概率为
_____。
5、一副扑克牌,从中任意抽出一张,求下列结果的概率:
① P(抽到红桃5)=____
②P(抽到大王或小王)=____
③P(抽到A)=____
④P(抽到方块)=____
6、如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止时, 指针指向B的概率是_____,
指向C或 D的概率是_____。
7.四张形状、大小、质地相同的卡片上分别画上圆、平行四边形、等边三角形、正方形,然后反扣在桌面上,洗匀后随机抽取一张,抽到轴对称图形的概率是( ),
抽到中心对称图形的概率是( )。
课堂小结:
2、必然事件A,则P(A)=1;
不可能事件B,则P(B)=0;
随机事件C,则0< P(C) <1。
1、概率的定义及基本性质。
如果在一次实验中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)=m/n。
0≤m≤n,有0 ≤ m/n≤1
新人教版九年级数学上册 25 概率初步
理解必然事件、不可能事件、随机事件的概念,能判断一件事情属于哪类事件;
在具体情境中了解概率的意义,计算一些简单随机事件的概率。
学习目标
天有不测风云
刮风
下雨
闪电
天晴
不看不知道,世界真奇妙
!
天有不测风云
思考:下列哪些现象是必然发生的,
哪些现象是不可能发生的?
太阳东升西落!
测量某天气温,结果为
-150°C!
今年是2018年!
两个正实数相加,
结果为负!
(不可能发生)
(必然发生)
(必然发生)
(不可能发生)
试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?
可能发生, 也可能不发生
必然发生
必然不会发生
小明从盒中任意摸出一球,
一定能摸到红球吗?
小麦从盒中摸出的球一定是白球吗?
小米从盒中摸出的球一定是红球吗?
三人每次都能摸到红球吗?
在自然界和实际生活中,我们会遇到各种各样的现象.
如果从结果能否预知的角度来看,可以分为两大类:
另一类现象的结果是无法预知的,即在一定的条件下,出现那种结果是无法预先确定的,这类现象称为随机现象.
一类现象的结果总是确定的,即在一定的条件下,它所出现的结果是可以预知的,这类现象称为确定性现象;
在一定条件下:
必然会发生的事件叫做必然事件;
必然不会发生的事件或者不可能发生的事件叫做不可能事件;
可能会发生,也可能不发生的事件叫做不确定事件或随机事件.
特征:事先不能预料即具有不确定性。
1.将一小勺白糖放入一杯温水中,并用筷子不断的搅拌,白糖溶解.
2.测量某天的最低气温,结果为—350℃.
3.小强打开电视机,电视里正在播放广告.
4.互为相反数的两个数的和等于0.
5.下过一场雨后,天空上出现一条彩虹.
不可能事件
必然事件
随机事件
判断下列事件中哪些是必然事件,哪些是不可能事件,哪些是随机事件.
例 题
必然事件
随机事件
1、在地球上,太阳每天从东方升起.
2、有一匹马奔跑的速度是70千米/秒.
3、明天,我买一注体育彩票,得500万大奖.
判断下列事件中哪些是必然事件,哪些是不可能事件,哪些是随机事件?
4、用长为3cm、4cm、7cm的三条线段首尾顺次连结,构成一个三角形.
5、掷一枚均匀的硬币,正面朝上.
跟踪训练
必然事件
不可能事件
随机事件
不可能事件
随机事件
8、人在月球上所受的重力比地球上小.
9、明年我市十·一的最高气温是三十摄氏度.
7、在标准大气压下,温度在0摄氏度以下,纯净水会结成冰.
6、2018年12月12日当天我市下雨.
随机事件
必然事件
随机事件
必然事件
1.下列事件是随机事件的是( )
A.人长生不老.
B.2018年世界杯巴西队必夺冠.
C.一个星期为七天.
D. 掷两枚质地均匀的正方体骰子朝上一面的点数之
积为36.
D
【解析】
2.(杭州·中考)“a是实数,则 ”这一事件是
A. 必然事件 B. 不确定事件
C. 不可能事件 D. 随机事件
3.(晋江·中考)下列事件中,是确定事件的是( )
A.打雷后会下雨 B.明天是睛天
C.1小时等于60分钟 D.下雨后有彩虹
【解析】选C.ABD都是不确定事件,C是确定事件.
选A.a是实数, 则 ,是必然事件.
课堂小结
4、一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小可能不同。
1、在一定条件下必然要发生的事件叫必 然事件.
2、在一定条件下不可能发生的事件叫不可能事件.
3、在一定条件下可能发生也可能不发生的事件叫随机事件.
可能的结果有1,2,3,4,5等5种,由于纸签的形状,大小相同,又是随机抽取的,所以我们可以认为:每个号被抽到的可能性相等,都是
试验1.从分别标有1.2.3.4.5号的5根纸签中随机抽取一根,抽出的签上的标号有几种可能?每一种抽取的可能性大小相等么?
试验2.抛掷一个骰子,它落地时向上的数有几种可能?分别是什么?发生的可能性大小一样吗?是多少?
6种等可能的结果:1,2,3,4,5,6.由于骰子的构造相同,质地均匀,又是随机掷出的,所以,每种结果的可能性相等,
都是
归纳
一般地,对于一个随机事件A,把刻画其发生可能性大小的数值,称之为随机事件A发生的概率。记为P(A)
共同特征: 1.每一次试验中,可能出现的结果只有有限个。2. 每一次试验中,各种结果出现的可能性相等。
概率从数量上刻画了一个随机事件发生的可能性的大小。
具有这些特点的试验称为古典概率.在这些试验中出现的事件为等可能事件.
例如,在上面抽签试验中,“抽到1号”这个事件包含____种可能结果,在全部___种可能的结果中所占的比为
______,于是这个事件的概率为
___ ___
1
5
“抽到偶数号”这个事件包含抽到( )和( )这( )种可能结果,在全部5种可能结果中所占的比为( ),于是这个事件的概率
2
4
2
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率 .
等可能事件概率的求法
1、当A是必然发生的事件时,P(A)是多少 ?
2、当A是不可能发生的事件时,P(A)是多少?
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能事件
必然事件
概率的值
不可能事件,必然事件与随机事件的关系
想一想
必然事件发生的可能性是
100%
,P(A)=1;
不可能事件发生的可能性是
0;
P(A)= 0;
3、不确定事件发生的可能性是大于0而小于1的.
即随机事件的概率为
由定义可知:
(1)概率反映了随机事件发生的可能性的大小。事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0;
(2)必然事件的概率为1,不可能事件的概率为0.因此 .
(3)随机事件的概率为
例1.掷一枚骰子,观察向上的一面的点数,求下列事件的概率。
①点数为2.
P(点数为2)=
②点数为奇数。
P(点数为奇数)=
③点数大于2且小于5.
P(点数大于2且小于5)=
例1变式 掷1个质地均匀的正方体骰子,观察向上一面的点数,
(1)求掷得点数为2或4或6的概率;
(2)小明在做掷骰子的试验时,前五次都没掷得点数2,求他第六次掷得点数2的概率。
例2.如图:是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率。
(1)P(指向红色)=_____
(2)P(指向红色或黄色)=_______
(3)P(不指向红色)= ________
1.明天下雨的概率为95%,那么
下列说法错误的是( )
(A) 明天下雨的可能性较大
(B) 明天不下雨的可能性较小
(C) 明天有可能是晴天
(D) 明天不可能是晴天
练习:
D
2、1袋子里有1个红球,3个白球和5个黄球,每一个球除颜色外都相同,从中任意摸出一个球,则
P(摸到红球)= ;
P(摸到白球)= ;
P(摸到黄球)= 。
1
-
9
1
-
3
5
-
9
3、有5张数字卡片,它们的背面完全相同,正面分别标有1,2,2,3,4。现将它们的背面朝上,从中任意摸到一张卡片,则:
p (摸到1号卡片)= ;
p (摸到2号卡片)= ;
p (摸到奇数号卡片)= ;
P(摸到偶数号卡片) = .
4、设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只,则从中任意取1只,是二等品的概率为
_____。
5、一副扑克牌,从中任意抽出一张,求下列结果的概率:
① P(抽到红桃5)=____
②P(抽到大王或小王)=____
③P(抽到A)=____
④P(抽到方块)=____
6、如图,能自由转动的转盘中, A、B、C、D四个扇形的圆心角的度数分别为180°、 30 °、 60 °、 90 °,转动转盘,当转盘停止时, 指针指向B的概率是_____,
指向C或 D的概率是_____。
7.四张形状、大小、质地相同的卡片上分别画上圆、平行四边形、等边三角形、正方形,然后反扣在桌面上,洗匀后随机抽取一张,抽到轴对称图形的概率是( ),
抽到中心对称图形的概率是( )。
课堂小结:
2、必然事件A,则P(A)=1;
不可能事件B,则P(B)=0;
随机事件C,则0< P(C) <1。
1、概率的定义及基本性质。
如果在一次实验中,有n种可能的结果,并且他们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)=m/n。
0≤m≤n,有0 ≤ m/n≤1
同课章节目录
