人教版数学七年级上册3.4 方案问题1(共19张ppt)
文档属性
| 名称 | 人教版数学七年级上册3.4 方案问题1(共19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 15:31:59 | ||
图片预览




文档简介
(共19张PPT)
资费繁多人眼迷,
实惠才是硬道理。
老师今日有困惑,
恳请大家出主意。
求 助
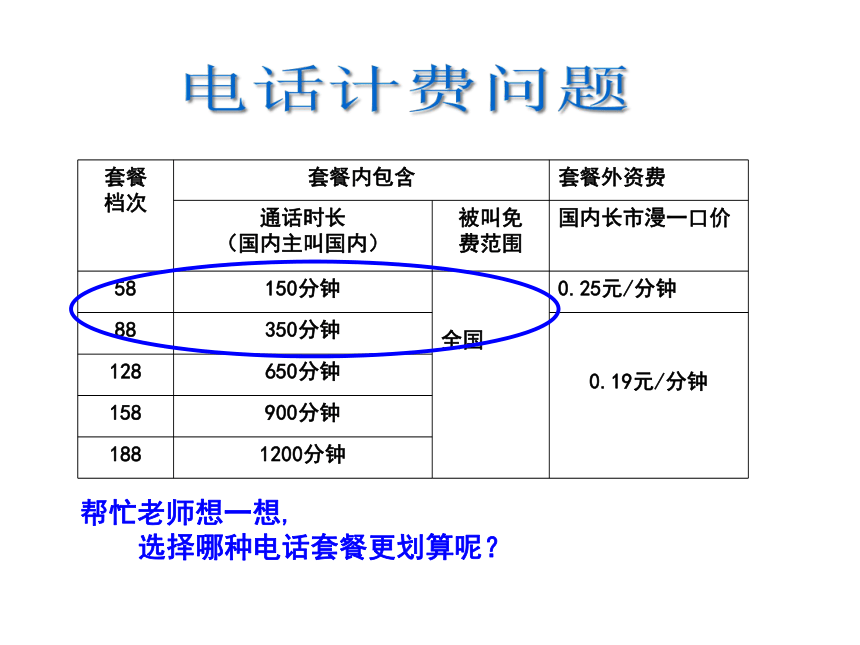
套餐
档次 套餐内包含 套餐外资费
通话时长
(国内主叫国内) 被叫免
费范围 国内长市漫一口价
58 150分钟
全国
0.25元/分钟
88 350分钟
0.19元/分钟
128 650分钟
158 900分钟
188 1200分钟
帮忙老师想一想,
选择哪种电话套餐更划算呢?
活动1.对问题的初步探究
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
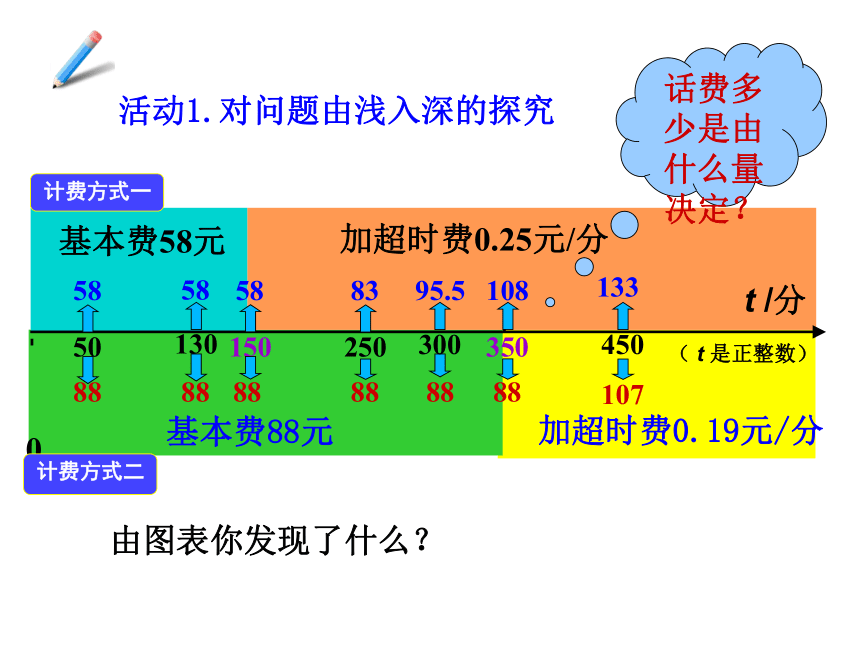
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
133
83
107
108
88
88
88
58
88
58
( t 是正整数)
t /分
话费多少是由什么量决定?
活动1.对问题由浅入深的探究
计费方式二
计费方式一
88
58
95.5
88
450
300
250
50
130
由图表你发现了什么?
活动2.对问题的深入探究
主叫时间
t/分
方式一
费用(元)
方式二
费用(元)
t=150
t=350
t<150
t>350
15058
88
108
88
58
88
88
58+0.25(t-150)
58+0.25(t-150)
88+0.19(t-350)
108+0.25(t-350)
划算
划算
划算
划算
设月主叫时间为t分钟.
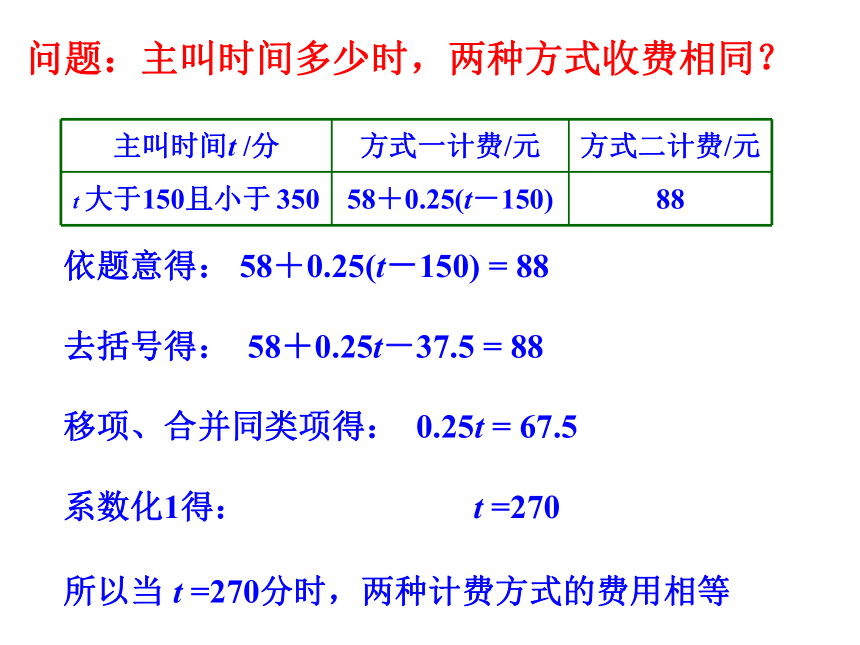
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
所以当 t =270分时,两种计费方式的费用相等
问题:主叫时间多少时,两种方式收费相同?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
活动2.对问题的深入探究
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
活动2.对问题的深入探究
问题6:综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式一方式二一样;
时,选择方式二省钱.
t 小于 270分
t 大于 270分
t 等于 270分
(1)探究解题的过程大致包含哪几个步骤?
(2)电话计费问题的核心问题是什么?
归纳小结
碰到方案做选择,
分类讨论最贴切.
首先找准关键点,
不重不漏是原则.
生活中常会碰到一些最优化问题,怎样走最近的路,怎样最省时间,怎样最省财力,怎样围最大的面积等,对于这类问题我们通过全面细致地考虑,利用数学中的分类思想、方程思想对几种方案进行比较,就一定能找到最佳方案。
最近的路
最省时间
最省财力
最大的面积
活动3 学以致用
用A4纸在某印社复印文件,复印页数不超过 20页时每页收费0.12元;复印页数超过20页 时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.复印的页数为多少时,两处的收费相同? (复印的页数不为零)
复印页数x 印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x张,依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,
图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格
便宜;
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,印社价格便宜.
综上所述:当x小于60页时,图书馆价格便宜;
当 x等于60页时,两家一样;
当x大于60时,印社价格便宜.
本节课的学习,让你感受最深的是什么?
(1)必做题:方案活页
(2)选做题:优化设计P465、P487
活动4 课后延展
调查市面的电话计费方式,
回家询问家长的手机缴费方式及
每月通话时间,应用今天所学的
知识给家长合理的建议。
七年级(1)(2)两班本周末准备观看电影,由各班班长负责买票,票价每张30元,1班班长问售票员买团体票是否可以优惠,售票员说: 30人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;
方案二:若打9折,有5人可免票。
①1班有48名学生,他该选择哪个方案?
②2班班长思考一会儿,说:我们班无论选择哪种方案,要付的钱是一样的。你知道2班有几人吗?
谢谢!
资费繁多人眼迷,
实惠才是硬道理。
老师今日有困惑,
恳请大家出主意。
求 助
套餐
档次 套餐内包含 套餐外资费
通话时长
(国内主叫国内) 被叫免
费范围 国内长市漫一口价
58 150分钟
全国
0.25元/分钟
88 350分钟
0.19元/分钟
128 650分钟
158 900分钟
188 1200分钟
帮忙老师想一想,
选择哪种电话套餐更划算呢?
活动1.对问题的初步探究
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
133
83
107
108
88
88
88
58
88
58
( t 是正整数)
t /分
话费多少是由什么量决定?
活动1.对问题由浅入深的探究
计费方式二
计费方式一
88
58
95.5
88
450
300
250
50
130
由图表你发现了什么?
活动2.对问题的深入探究
主叫时间
t/分
方式一
费用(元)
方式二
费用(元)
t=150
t=350
t<150
t>350
150
88
108
88
58
88
88
58+0.25(t-150)
58+0.25(t-150)
88+0.19(t-350)
108+0.25(t-350)
划算
划算
划算
划算
设月主叫时间为t分钟.
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
所以当 t =270分时,两种计费方式的费用相等
问题:主叫时间多少时,两种方式收费相同?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
活动2.对问题的深入探究
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
计费方式一
计费方式二
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
活动2.对问题的深入探究
问题6:综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式一方式二一样;
时,选择方式二省钱.
t 小于 270分
t 大于 270分
t 等于 270分
(1)探究解题的过程大致包含哪几个步骤?
(2)电话计费问题的核心问题是什么?
归纳小结
碰到方案做选择,
分类讨论最贴切.
首先找准关键点,
不重不漏是原则.
生活中常会碰到一些最优化问题,怎样走最近的路,怎样最省时间,怎样最省财力,怎样围最大的面积等,对于这类问题我们通过全面细致地考虑,利用数学中的分类思想、方程思想对几种方案进行比较,就一定能找到最佳方案。
最近的路
最省时间
最省财力
最大的面积
活动3 学以致用
用A4纸在某印社复印文件,复印页数不超过 20页时每页收费0.12元;复印页数超过20页 时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.复印的页数为多少时,两处的收费相同? (复印的页数不为零)
复印页数x 印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:设复印页数为x张,依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,
图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格
便宜;
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,印社价格便宜.
综上所述:当x小于60页时,图书馆价格便宜;
当 x等于60页时,两家一样;
当x大于60时,印社价格便宜.
本节课的学习,让你感受最深的是什么?
(1)必做题:方案活页
(2)选做题:优化设计P465、P487
活动4 课后延展
调查市面的电话计费方式,
回家询问家长的手机缴费方式及
每月通话时间,应用今天所学的
知识给家长合理的建议。
七年级(1)(2)两班本周末准备观看电影,由各班班长负责买票,票价每张30元,1班班长问售票员买团体票是否可以优惠,售票员说: 30人以上的团体票有两个优惠方案可选择:
方案一:全体人员可打8折;
方案二:若打9折,有5人可免票。
①1班有48名学生,他该选择哪个方案?
②2班班长思考一会儿,说:我们班无论选择哪种方案,要付的钱是一样的。你知道2班有几人吗?
谢谢!
