人教版数学七年级上册4.3.2角的比较与计算 课件1(共21张ppt)
文档属性
| 名称 | 人教版数学七年级上册4.3.2角的比较与计算 课件1(共21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 15:45:10 | ||
图片预览





文档简介
一、本节课主要知识点:
1、角的大小的比较;
2、角的平分线的定义;
3、角的和差表示;
4、简单的角度的和差计算。
二、教学过程
活动1 创设情境
(一)复习回顾:线段的大小比较有哪些方法?
1.从“形”出发,利用线段移动叠合的方法
A
B
A
C
2.以“数” 出发,通过度量长度进行数值大 小比较。
二、教学过程
活动1 创设情境
有一天学生张靓和王帅各带了一把折扇(状态如下),下面是他们的一段对话:
张靓:我的折扇张开大一些,所以我的折扇的角也大一些.
王帅:我的折扇长一些,所以我的折扇的角也大一些.
(二)导入新课:《折扇的故事》
活动1 创设情境
二、教学过程
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小呢?
活动2 分组自学
二、教学过程
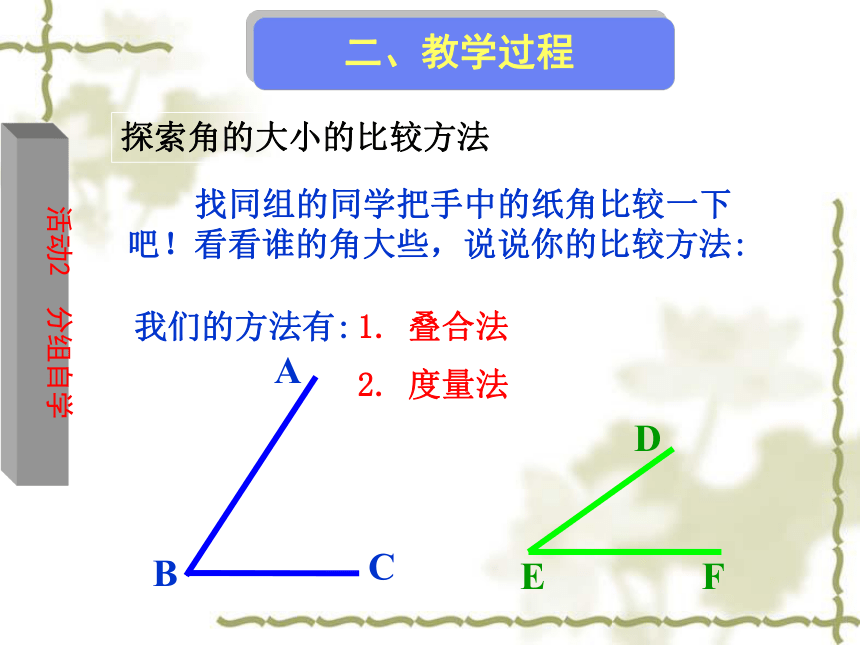
探索角的大小的比较方法
找同组的同学把手中的纸角比较一下吧!看看谁的角大些,说说你的比较方法:
B
A
C
E
D
F
我们的方法有:
2. 度量法
1. 叠合法
二、教学过程
活动2 分组自学
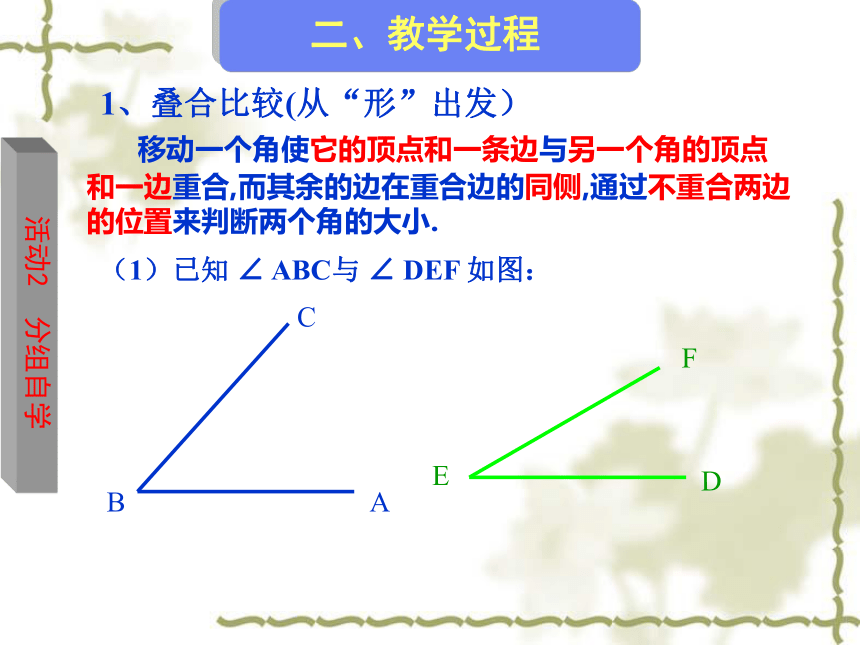
1、叠合比较(从“形”出发)
(1)已知 ∠ ABC与 ∠ DEF 如图:
D
E
F
A
B
C
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
二、教学过程
活动2 分组自学
A
B
C
F
( E)
( D)
A
B
C
( E)
( D)
( F )
A
B
C
F
( E )
( D )
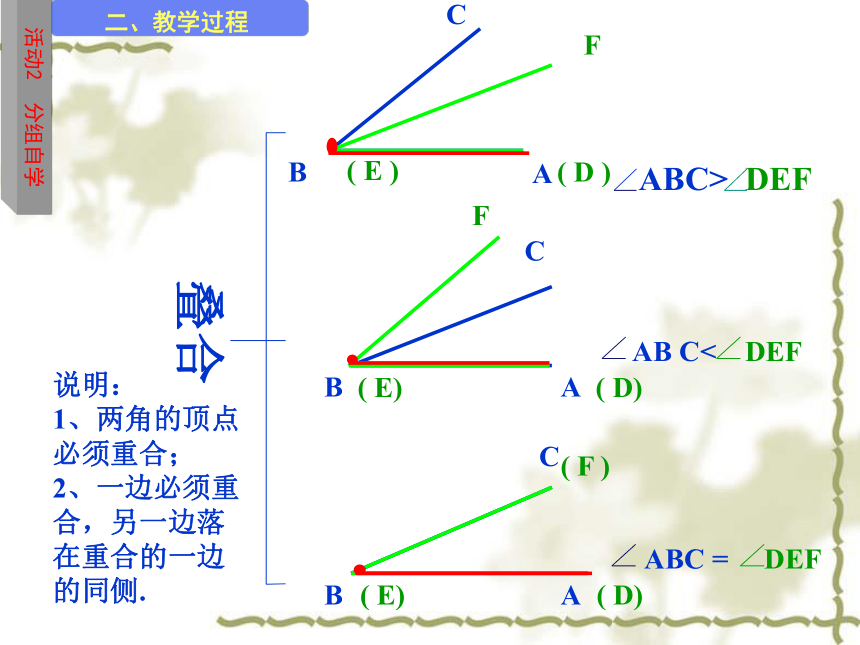
叠合
ABC> DEF
AB C< DEF
ABC = DEF
说明:
1、两角的顶点
必须重合;
2、一边必须重
合,另一边落
在重合的一边
的同侧.
二、教学过程
活动2 分组自学
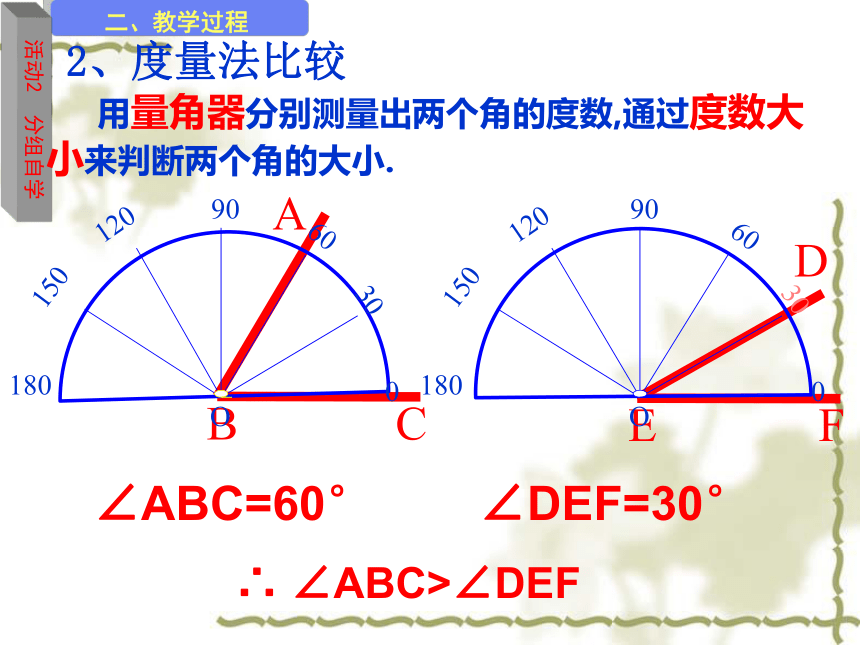
2、度量法比较
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴ ∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
二、教学过程
活动2 分组自学
回到开始的问题,张靓和王帅同学的对话中说的折扇的大小和长短能判断角的大小吗?
结论:角的两边张开越大,角就越大,与所画边的长短无关。
二、教学过程
活动2 分组自学
三、角的和差的表示
已知两个角 1和 2( 1 > 2 ),
把它们的顶点和一边重合,看看这两种情况:
1
2
A
O
B
B
O
C
二、教学过程
活动2 分组自学
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
AOC为 1 和 2 的和
记作 AOC = 1 + 2
(
)
AOC为 1 和 2 的差
记作 AOC = 1 – 2
(
)
顶点与一边重合
二、教学过程
活动2 分组自学
B
O
C
A
叫做这个角的角平分线。 你,记住了吗?
四、角平分线
把手上的纸角对折,使其两边重
合,折痕两边所成的两个角的大小
有什么关系? 来,动动手吧!
OB 平分 AOC ( 已知 )
AOB = BOC = AOC
或 AOC=2 AOB=2 BOC( 角平分线定义 )
二、教学过程
活动3 合作探究
看教学稿上《活动3》,在小组内讨论完成《活动3》的4个问题,比一比,看哪个小组完成得又快又好!等会儿我们可要在全班展示哟!
二、教学过程
活动4 交流矫正
1、如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
分析:∵∠AOC=∠AOB+∠BOC , ∠BOD=∠COD + ∠BOC
∴∠AOC=∠BOD
二、教学过程
活动4 交流矫正
A
B
D
C
( 1 ) DAB = DAC+
( 2 ) ACB = DCB –
CAB
DCA
二、教学过程
活动4 交流矫正
A
B
C
D
E
AD是 BAC的平分线
=
ABC = 2 ABE
平分
( 角平分线的定义 )
BAD
CAD
BE
ABC
( 角平分线的定义 )
3、填空。
想一想
二、教学过程
活动4 交流矫正
A
B
C
D
O
4、如图 ∠AOB=∠BOC=∠COD,
则OB 是 的平分线,
= ∠AOC,
= ∠BOD
∠BOC =
= `
AOC
BOC
BOC
AOD
BOD
AOD
此时OB、OC叫∠ AOD的三等份线
二、教学过程
活动5 当堂训练
训练A : 见教学稿《当堂训练5:训练A 1、2》
训练B : 见教学稿《当堂训练5:训练B 3》
分层作业,提升能力
温馨提示:
《训练A》每名同学都必须完成,不怕困难的同学接着完成《训练B》,敢于挑战自己的同学,试试《课外思考》吧!
课堂小结,提高认识
交流一下对本节课的认识吧!对学习内容、学习的重难点谈谈自己的心得体会。
活动6 小结辅导
二、教学过程
1、角的大小比较方法有哪些?
4、角的简单的和差计算……
2、角的大小关系有哪些?
3、三角板可拼出哪些角?
1、角的大小的比较;
2、角的平分线的定义;
3、角的和差表示;
4、简单的角度的和差计算。
二、教学过程
活动1 创设情境
(一)复习回顾:线段的大小比较有哪些方法?
1.从“形”出发,利用线段移动叠合的方法
A
B
A
C
2.以“数” 出发,通过度量长度进行数值大 小比较。
二、教学过程
活动1 创设情境
有一天学生张靓和王帅各带了一把折扇(状态如下),下面是他们的一段对话:
张靓:我的折扇张开大一些,所以我的折扇的角也大一些.
王帅:我的折扇长一些,所以我的折扇的角也大一些.
(二)导入新课:《折扇的故事》
活动1 创设情境
二、教学过程
同学们,你们有办法帮他们进行判断吗?
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小呢?
活动2 分组自学
二、教学过程
探索角的大小的比较方法
找同组的同学把手中的纸角比较一下吧!看看谁的角大些,说说你的比较方法:
B
A
C
E
D
F
我们的方法有:
2. 度量法
1. 叠合法
二、教学过程
活动2 分组自学
1、叠合比较(从“形”出发)
(1)已知 ∠ ABC与 ∠ DEF 如图:
D
E
F
A
B
C
移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
二、教学过程
活动2 分组自学
A
B
C
F
( E)
( D)
A
B
C
( E)
( D)
( F )
A
B
C
F
( E )
( D )
叠合
ABC> DEF
AB C< DEF
ABC = DEF
说明:
1、两角的顶点
必须重合;
2、一边必须重
合,另一边落
在重合的一边
的同侧.
二、教学过程
活动2 分组自学
2、度量法比较
C
A
B
O
30
0
60
90
120
150
180
∠ABC=60°
F
D
E
O
30
0
60
90
120
150
180
∠DEF=30°
∴ ∠ABC>∠DEF
用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
二、教学过程
活动2 分组自学
回到开始的问题,张靓和王帅同学的对话中说的折扇的大小和长短能判断角的大小吗?
结论:角的两边张开越大,角就越大,与所画边的长短无关。
二、教学过程
活动2 分组自学
三、角的和差的表示
已知两个角 1和 2( 1 > 2 ),
把它们的顶点和一边重合,看看这两种情况:
1
2
A
O
B
B
O
C
二、教学过程
活动2 分组自学
1
O
A
B
2
C
B
O
A
1
B
O
O
B
C
2
AOC为 1 和 2 的和
记作 AOC = 1 + 2
(
)
AOC为 1 和 2 的差
记作 AOC = 1 – 2
(
)
顶点与一边重合
二、教学过程
活动2 分组自学
B
O
C
A
叫做这个角的角平分线。 你,记住了吗?
四、角平分线
把手上的纸角对折,使其两边重
合,折痕两边所成的两个角的大小
有什么关系? 来,动动手吧!
OB 平分 AOC ( 已知 )
AOB = BOC = AOC
或 AOC=2 AOB=2 BOC( 角平分线定义 )
二、教学过程
活动3 合作探究
看教学稿上《活动3》,在小组内讨论完成《活动3》的4个问题,比一比,看哪个小组完成得又快又好!等会儿我们可要在全班展示哟!
二、教学过程
活动4 交流矫正
1、如图,用〝=〞或 〝>〞或 〝<〞填空
D
O
C
B
A
=
>
=
<
=
分析:∵∠AOC=∠AOB+∠BOC , ∠BOD=∠COD + ∠BOC
∴∠AOC=∠BOD
二、教学过程
活动4 交流矫正
A
B
D
C
( 1 ) DAB = DAC+
( 2 ) ACB = DCB –
CAB
DCA
二、教学过程
活动4 交流矫正
A
B
C
D
E
AD是 BAC的平分线
=
ABC = 2 ABE
平分
( 角平分线的定义 )
BAD
CAD
BE
ABC
( 角平分线的定义 )
3、填空。
想一想
二、教学过程
活动4 交流矫正
A
B
C
D
O
4、如图 ∠AOB=∠BOC=∠COD,
则OB 是 的平分线,
= ∠AOC,
= ∠BOD
∠BOC =
= `
AOC
BOC
BOC
AOD
BOD
AOD
此时OB、OC叫∠ AOD的三等份线
二、教学过程
活动5 当堂训练
训练A : 见教学稿《当堂训练5:训练A 1、2》
训练B : 见教学稿《当堂训练5:训练B 3》
分层作业,提升能力
温馨提示:
《训练A》每名同学都必须完成,不怕困难的同学接着完成《训练B》,敢于挑战自己的同学,试试《课外思考》吧!
课堂小结,提高认识
交流一下对本节课的认识吧!对学习内容、学习的重难点谈谈自己的心得体会。
活动6 小结辅导
二、教学过程
1、角的大小比较方法有哪些?
4、角的简单的和差计算……
2、角的大小关系有哪些?
3、三角板可拼出哪些角?
