2020-2021学年山东省烟台市龙口市八年级(上)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省烟台市龙口市八年级(上)期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 120.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 06:21:25 | ||
图片预览




文档简介
2020-2021学年山东省烟台市龙口市八年级(上)期中数学试卷(五四学制)
一.选择题(共12小题)
1.(3分)下列变形,是因式分解的是( )
A.x2+3x﹣16=(x﹣2)(x+5)﹣6
B.x2﹣16=(x+4)(x﹣4)
C.(x﹣1)2=x2﹣2x+1
D.
2.(3分)下列分式中是最简分式的是( )
A.
B.
C.
D.
3.(3分)如果a2+mab+9b2是一个完全平方式,则m应是( )
A.3
B.±3
C.6
D.±6
4.(3分)若分式的值为0,则x的值为( )
A.4
B.﹣4
C.±3
D.3
5.(3分)将多项式9xy2﹣4x因式分解,结果正确的是( )
A.xy(9y﹣4)
B.x(9y2﹣4)
C.x(3y﹣2)2
D.x(3y+2)(3y﹣2)
6.(3分)下列各式中不能用完全平方公式分解因式的是( )
A.﹣4x2+4xy﹣y2
B.x2﹣2x+1
C.x2﹣2x﹣1
D.
7.(3分)如果m为整数,那么使分式的值为整数的m的值有( )
A.2个
B.3个
C.4个
D.5个
8.(3分)如果x>y>0,那么的值是( )
A.零
B.正数
C.负数
D.整数
9.(3分)如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A.众数改变,方差改变
B.众数不变,平均数改变
C.中位数改变,方差不变
D.中位数不变,平均数不变
10.(3分)将分式方程1﹣=去分母后得( )
A.x2+x﹣5=x2+2x
B.x2+x﹣5=x+2
C.1﹣5=x+2
D.x﹣5=x+2
11.(3分)初三体育素质测试,某小组5名同学成绩如下所示,有两个数据遮盖,如图:
编号
1
2
3
4
5
方差
平均成绩
得分
38
34
■
37
40
■
37
那么被遮盖的两个数据依次是( )
A.35
2
B.36
4
C.35
3
D.36
3
12.(3分)4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a、b满足( )
A.2a=5b
B.2a=3b
C.a=3b
D.a=2b
二.填空题(共8小题)
13.(3分)一组数据6,2,5,3,x中,唯一的众数是x,中位数也是x,则x的值为
.
14.(3分)因式分解:x(x﹣2)﹣x+2=
.
15.(3分)若a+b=1,则a2﹣b2+2b﹣2=
.
16.(3分)若3x﹣1是多项式6x2+mx﹣1的一个因式,则m=
.
17.(3分)若关于x的分式方程+1有增根,则m=
.
18.(3分)关于x的分式方程+2=的解为正实数,则k的取值范围是
.
19.(3分)一项工程,甲乙合作b天能完成,甲单独做需要a天完成,则乙独做需
天完成.
20.(3分)已知S1=a+1(a不取0和﹣1),S2=,S3=,S4=,…按此规律,请用含a的代数式表示S2020=
.
三.解答题(共6小题)
21.计算:
(1)因式分解:4a(b+c)2﹣4a2(b+c)+a3;
(2)解分式方程:.
22.如图,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n(以上长度单位:cm)
(1)观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为
;
(2)若每块小长方形的周长是20m且每块大正方形与每块小正方形的面积差为40cm2,求这张长方形纸板的面积是多少平方厘米?
23.先化简,再求值(﹣)÷,其中a满足a2+3a﹣2=0.
24.先化简,(﹣x+1)÷,再选一个你喜欢的数代入求值.
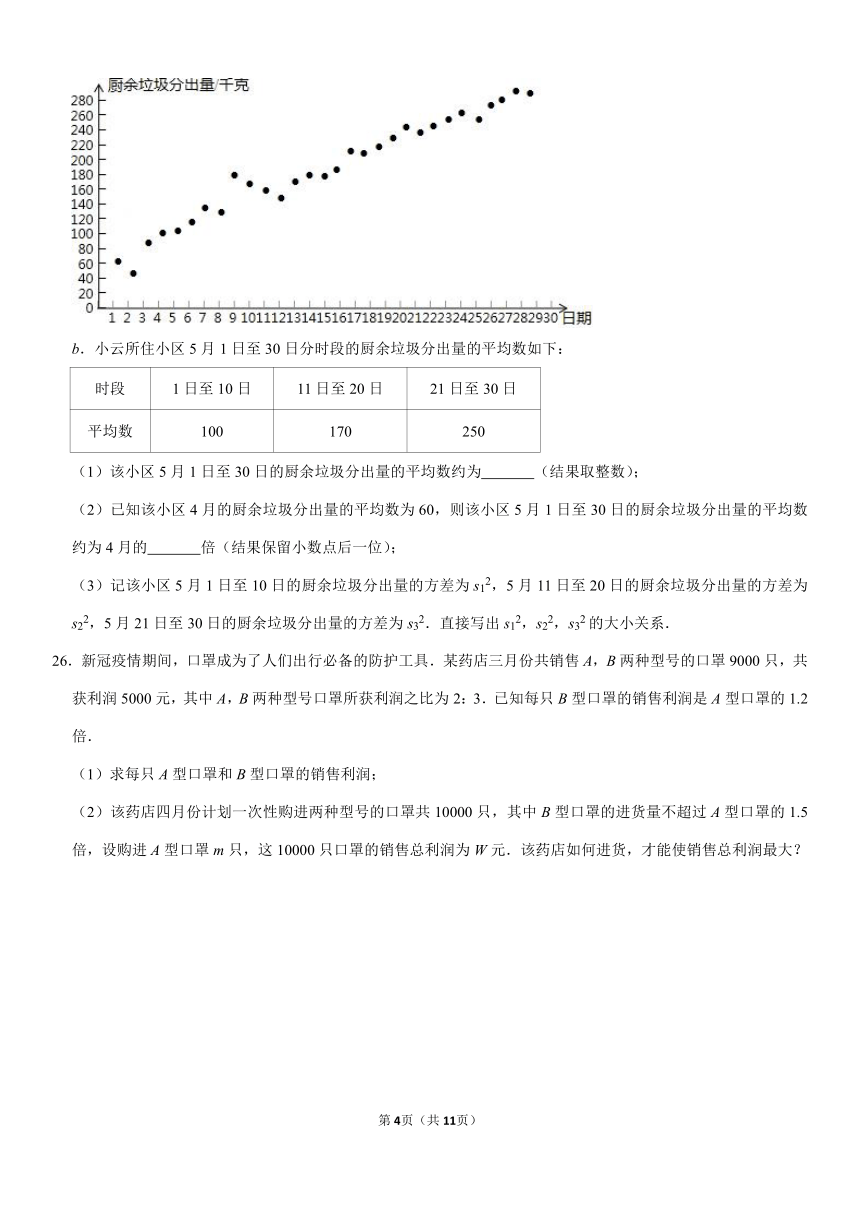
25.小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段
1日至10日
11日至20日
21日至30日
平均数
100
170
250
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为
(结果取整数);
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的
倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为s12,5月11日至20日的厨余垃圾分出量的方差为s22,5月21日至30日的厨余垃圾分出量的方差为s32.直接写出s12,s22,s32的大小关系.
26.新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店三月份共销售A,B两种型号的口罩9000只,共获利润5000元,其中A,B两种型号口罩所获利润之比为2:3.已知每只B型口罩的销售利润是A型口罩的1.2倍.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店四月份计划一次性购进两种型号的口罩共10000只,其中B型口罩的进货量不超过A型口罩的1.5倍,设购进A型口罩m只,这10000只口罩的销售总利润为W元.该药店如何进货,才能使销售总利润最大?
2020-2021学年山东省烟台市龙口市八年级(上)期中数学试卷(五四学制)
试题解析
一.选择题(共12小题)
1.解:A、结果不是整式相乘的形式;
B、正确;
C、是整式的乘法,故选项错误;
D、结果不是整式相乘的形式.
故选:B.
2.解:A.==,不符合题意;
B.=,不符合题意;
C.==,不符合题意;
D.是最简分式;
故选:D.
3.解:∵a2+mab+9b4是一个完全平方式,
∴m=±6,
故选:D.
4.解:根据题意得:,
解得:x=3.
故选:D.
5.解:9xy2﹣6x=x(3y+2)(6y﹣2).
故选:D.
6.解:A、﹣4x2+7xy﹣y2=﹣(4x8﹣4xy+y2)=﹣(6x﹣y)2,故选项错误;
B、x2﹣2x+1=(x﹣1)7,故选项错误;
C、不能分解;
D、x6﹣x+=3﹣36x+9)=(7x﹣3)2,故选项错误.
故选:C.
7.解:∵=5+,
若原分式的值为整数,那么m+8=﹣2,1或6.
由m+1=﹣2得m=﹣7;
由m+1=﹣1得m=﹣3;
由m+1=1得m=3;
由m+1=2得m=6.
∴m=﹣3,﹣2,6,1.
8.解:原式==,
∵x>y>0,
∴原式不是8,也不是负数,一定是正数.
故选:B.
9.解:如果将一组数据中的每个数都减去5,那么所得的一组新数据的众数、平均数都减少5,
故选:C.
10.解:去分母得:x(x+1)﹣5=x(x+5),
去括号得:x2+x﹣5=x8+2x.
故选:A.
11.解:∵这组数据的平均数是37,
∴编号3的得分是:37×5﹣(38+34+37+40)=36;
被遮盖的方差是:[(38﹣37)2+(34﹣37)6+(36﹣37)2+(37﹣37)2+(40﹣37)2]=4;
故选:B.
12.解:S1=b(a+b)×2+2=a5+2b2,
S2=(a+b)2﹣S1=(a+b)3﹣(a2+2b3)=2ab﹣b2,
∵S5=2S2,
∴a4+2b2=5(2ab﹣b2),
整理,得(a﹣4b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:D.
二.填空题(共8小题)
13.解:其余4个数据按顺序排列为:2,4,5,6,
∵x是中位数,也是众数,
∴x=8或x=5.
故答案为:3或5.
14.解:原式=x(x﹣2)﹣(x﹣2)=(x﹣8)(x﹣1).
故答案为:(x﹣2)(x﹣7).
15.解:∵a+b=1,
∴a2﹣b8+2b﹣2
=(a+b)(a﹣b)+8b﹣2
=a﹣b+2b﹣2
=a+b﹣2
=1﹣2
=﹣1.
故答案为:﹣1.
16.解:若3x﹣1是多项式4x2+mx﹣1的一个因式,得
2x2+mx﹣1=(3x﹣1)(2x+2).
解得m=1,
故答案为:1.
17.解:去分母得:3x=m+3+(x﹣8),整理得:2x=m+1,
∵关于x的分式方程有增根,
∴x=2,
把x=4代入到2x=m+1中得:8×2=m+1,
解得:m=3;
故答案为:3.
18.解:方程+7=,得
4+2(x﹣2)=k﹣5,
解得,x=,
∵≠2,
∴k≠4,
由题意得,>7,
解得,k>﹣2,
∴k的取值范围是k>﹣2且k≠2.
故答案为:k>﹣2且k≠2.
19.解:设乙乙独做需x天,根据题意得:
b(+)=3,
解得:x=.
故乙独做需天完成.
故答案为:.
20.解:∵S1=a+1(a不取8和﹣1),
∴S2==﹣,
S3==,
S3==a+1,
…,
∴3个一循环,
∵2020÷6=673…1,
∴S2020=a+1.
故答案为:a+7.
三.解答题(共6小题)
21.解:(1)原式=a[4(b+c)2﹣3a(b+c)+a2]
=a[2(b+c)﹣a]2
=a(2b+2c﹣a)6.
(2)两边同时乘以最简公分母(x﹣1),
可得2(x﹣4)+x﹣1=﹣2,
解得x=4,
检验:当x=1时,x﹣1=3,
所以x=2是原方程的增根,
原方程无解.
22.解:(1)由图形可知,2m2+5mn+2n2=(3m+n)(m+2n),
故答案为(2m+n)(m+8n);
(2)∵m2﹣n2=40,
∴(m+n)(m﹣n)=40,
∵m+n=20÷2=10,
∴m﹣n=4,
解得m=7,n=4,
∴2m+n=17,m+2n=13,
∴纸板的面积(8m+n)(m+2n)=17×13=221(平方厘米).
答:纸板的面积为221平方厘米.
23.解:(﹣)÷
=[]
=()
=
=
=,
∵a2+3a﹣4=0,
∴a2+6a=2,
∴原式==1.
24.解:原式==?=,
当x=0时,原式=1.
25.解:(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为≈173(千克),
故答案为:173;
(2)该小区8月1日至30日的厨余垃圾分出量的平均数约为4月的≈2.9(倍),
故答案为:2.7;
(3)由小云所住小区5月1日至30日的厨余垃圾分出量统计图知,第4个10天的分出量最分散,
∴s12>s62>s36.
26.解:设销售A型口罩x只,销售B型口罩y只
,解得,
经检验,x=4000,
∴每只A型口罩的销售利润为:(元).
答:每只A型口罩和B型口罩的销售利润分别为0.4元,0.6元.
(2)根据题意得,W=7.5m+0.3(10000﹣m)=﹣0.1m+6000,
10000﹣m≤3.5m,解得m≥4000,
∵﹣0.3<0,
∴W随m的增大而减小,
∵m为正整数,
∴当m=4000时,W取最大值,
即药店购进A型口罩4000只、B型口罩6000只,最大利润为5600元.
第1页(共1页)
一.选择题(共12小题)
1.(3分)下列变形,是因式分解的是( )
A.x2+3x﹣16=(x﹣2)(x+5)﹣6
B.x2﹣16=(x+4)(x﹣4)
C.(x﹣1)2=x2﹣2x+1
D.
2.(3分)下列分式中是最简分式的是( )
A.
B.
C.
D.
3.(3分)如果a2+mab+9b2是一个完全平方式,则m应是( )
A.3
B.±3
C.6
D.±6
4.(3分)若分式的值为0,则x的值为( )
A.4
B.﹣4
C.±3
D.3
5.(3分)将多项式9xy2﹣4x因式分解,结果正确的是( )
A.xy(9y﹣4)
B.x(9y2﹣4)
C.x(3y﹣2)2
D.x(3y+2)(3y﹣2)
6.(3分)下列各式中不能用完全平方公式分解因式的是( )
A.﹣4x2+4xy﹣y2
B.x2﹣2x+1
C.x2﹣2x﹣1
D.
7.(3分)如果m为整数,那么使分式的值为整数的m的值有( )
A.2个
B.3个
C.4个
D.5个
8.(3分)如果x>y>0,那么的值是( )
A.零
B.正数
C.负数
D.整数
9.(3分)如果将一组数据中的每个数都减去5,那么所得的一组新数据( )
A.众数改变,方差改变
B.众数不变,平均数改变
C.中位数改变,方差不变
D.中位数不变,平均数不变
10.(3分)将分式方程1﹣=去分母后得( )
A.x2+x﹣5=x2+2x
B.x2+x﹣5=x+2
C.1﹣5=x+2
D.x﹣5=x+2
11.(3分)初三体育素质测试,某小组5名同学成绩如下所示,有两个数据遮盖,如图:
编号
1
2
3
4
5
方差
平均成绩
得分
38
34
■
37
40
■
37
那么被遮盖的两个数据依次是( )
A.35
2
B.36
4
C.35
3
D.36
3
12.(3分)4张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a、b满足( )
A.2a=5b
B.2a=3b
C.a=3b
D.a=2b
二.填空题(共8小题)
13.(3分)一组数据6,2,5,3,x中,唯一的众数是x,中位数也是x,则x的值为
.
14.(3分)因式分解:x(x﹣2)﹣x+2=
.
15.(3分)若a+b=1,则a2﹣b2+2b﹣2=
.
16.(3分)若3x﹣1是多项式6x2+mx﹣1的一个因式,则m=
.
17.(3分)若关于x的分式方程+1有增根,则m=
.
18.(3分)关于x的分式方程+2=的解为正实数,则k的取值范围是
.
19.(3分)一项工程,甲乙合作b天能完成,甲单独做需要a天完成,则乙独做需
天完成.
20.(3分)已知S1=a+1(a不取0和﹣1),S2=,S3=,S4=,…按此规律,请用含a的代数式表示S2020=
.
三.解答题(共6小题)
21.计算:
(1)因式分解:4a(b+c)2﹣4a2(b+c)+a3;
(2)解分式方程:.
22.如图,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n(以上长度单位:cm)
(1)观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为
;
(2)若每块小长方形的周长是20m且每块大正方形与每块小正方形的面积差为40cm2,求这张长方形纸板的面积是多少平方厘米?
23.先化简,再求值(﹣)÷,其中a满足a2+3a﹣2=0.
24.先化简,(﹣x+1)÷,再选一个你喜欢的数代入求值.
25.小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
时段
1日至10日
11日至20日
21日至30日
平均数
100
170
250
(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为
(结果取整数);
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的
倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为s12,5月11日至20日的厨余垃圾分出量的方差为s22,5月21日至30日的厨余垃圾分出量的方差为s32.直接写出s12,s22,s32的大小关系.
26.新冠疫情期间,口罩成为了人们出行必备的防护工具.某药店三月份共销售A,B两种型号的口罩9000只,共获利润5000元,其中A,B两种型号口罩所获利润之比为2:3.已知每只B型口罩的销售利润是A型口罩的1.2倍.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店四月份计划一次性购进两种型号的口罩共10000只,其中B型口罩的进货量不超过A型口罩的1.5倍,设购进A型口罩m只,这10000只口罩的销售总利润为W元.该药店如何进货,才能使销售总利润最大?
2020-2021学年山东省烟台市龙口市八年级(上)期中数学试卷(五四学制)
试题解析
一.选择题(共12小题)
1.解:A、结果不是整式相乘的形式;
B、正确;
C、是整式的乘法,故选项错误;
D、结果不是整式相乘的形式.
故选:B.
2.解:A.==,不符合题意;
B.=,不符合题意;
C.==,不符合题意;
D.是最简分式;
故选:D.
3.解:∵a2+mab+9b4是一个完全平方式,
∴m=±6,
故选:D.
4.解:根据题意得:,
解得:x=3.
故选:D.
5.解:9xy2﹣6x=x(3y+2)(6y﹣2).
故选:D.
6.解:A、﹣4x2+7xy﹣y2=﹣(4x8﹣4xy+y2)=﹣(6x﹣y)2,故选项错误;
B、x2﹣2x+1=(x﹣1)7,故选项错误;
C、不能分解;
D、x6﹣x+=3﹣36x+9)=(7x﹣3)2,故选项错误.
故选:C.
7.解:∵=5+,
若原分式的值为整数,那么m+8=﹣2,1或6.
由m+1=﹣2得m=﹣7;
由m+1=﹣1得m=﹣3;
由m+1=1得m=3;
由m+1=2得m=6.
∴m=﹣3,﹣2,6,1.
8.解:原式==,
∵x>y>0,
∴原式不是8,也不是负数,一定是正数.
故选:B.
9.解:如果将一组数据中的每个数都减去5,那么所得的一组新数据的众数、平均数都减少5,
故选:C.
10.解:去分母得:x(x+1)﹣5=x(x+5),
去括号得:x2+x﹣5=x8+2x.
故选:A.
11.解:∵这组数据的平均数是37,
∴编号3的得分是:37×5﹣(38+34+37+40)=36;
被遮盖的方差是:[(38﹣37)2+(34﹣37)6+(36﹣37)2+(37﹣37)2+(40﹣37)2]=4;
故选:B.
12.解:S1=b(a+b)×2+2=a5+2b2,
S2=(a+b)2﹣S1=(a+b)3﹣(a2+2b3)=2ab﹣b2,
∵S5=2S2,
∴a4+2b2=5(2ab﹣b2),
整理,得(a﹣4b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:D.
二.填空题(共8小题)
13.解:其余4个数据按顺序排列为:2,4,5,6,
∵x是中位数,也是众数,
∴x=8或x=5.
故答案为:3或5.
14.解:原式=x(x﹣2)﹣(x﹣2)=(x﹣8)(x﹣1).
故答案为:(x﹣2)(x﹣7).
15.解:∵a+b=1,
∴a2﹣b8+2b﹣2
=(a+b)(a﹣b)+8b﹣2
=a﹣b+2b﹣2
=a+b﹣2
=1﹣2
=﹣1.
故答案为:﹣1.
16.解:若3x﹣1是多项式4x2+mx﹣1的一个因式,得
2x2+mx﹣1=(3x﹣1)(2x+2).
解得m=1,
故答案为:1.
17.解:去分母得:3x=m+3+(x﹣8),整理得:2x=m+1,
∵关于x的分式方程有增根,
∴x=2,
把x=4代入到2x=m+1中得:8×2=m+1,
解得:m=3;
故答案为:3.
18.解:方程+7=,得
4+2(x﹣2)=k﹣5,
解得,x=,
∵≠2,
∴k≠4,
由题意得,>7,
解得,k>﹣2,
∴k的取值范围是k>﹣2且k≠2.
故答案为:k>﹣2且k≠2.
19.解:设乙乙独做需x天,根据题意得:
b(+)=3,
解得:x=.
故乙独做需天完成.
故答案为:.
20.解:∵S1=a+1(a不取8和﹣1),
∴S2==﹣,
S3==,
S3==a+1,
…,
∴3个一循环,
∵2020÷6=673…1,
∴S2020=a+1.
故答案为:a+7.
三.解答题(共6小题)
21.解:(1)原式=a[4(b+c)2﹣3a(b+c)+a2]
=a[2(b+c)﹣a]2
=a(2b+2c﹣a)6.
(2)两边同时乘以最简公分母(x﹣1),
可得2(x﹣4)+x﹣1=﹣2,
解得x=4,
检验:当x=1时,x﹣1=3,
所以x=2是原方程的增根,
原方程无解.
22.解:(1)由图形可知,2m2+5mn+2n2=(3m+n)(m+2n),
故答案为(2m+n)(m+8n);
(2)∵m2﹣n2=40,
∴(m+n)(m﹣n)=40,
∵m+n=20÷2=10,
∴m﹣n=4,
解得m=7,n=4,
∴2m+n=17,m+2n=13,
∴纸板的面积(8m+n)(m+2n)=17×13=221(平方厘米).
答:纸板的面积为221平方厘米.
23.解:(﹣)÷
=[]
=()
=
=
=,
∵a2+3a﹣4=0,
∴a2+6a=2,
∴原式==1.
24.解:原式==?=,
当x=0时,原式=1.
25.解:(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为≈173(千克),
故答案为:173;
(2)该小区8月1日至30日的厨余垃圾分出量的平均数约为4月的≈2.9(倍),
故答案为:2.7;
(3)由小云所住小区5月1日至30日的厨余垃圾分出量统计图知,第4个10天的分出量最分散,
∴s12>s62>s36.
26.解:设销售A型口罩x只,销售B型口罩y只
,解得,
经检验,x=4000,
∴每只A型口罩的销售利润为:(元).
答:每只A型口罩和B型口罩的销售利润分别为0.4元,0.6元.
(2)根据题意得,W=7.5m+0.3(10000﹣m)=﹣0.1m+6000,
10000﹣m≤3.5m,解得m≥4000,
∵﹣0.3<0,
∴W随m的增大而减小,
∵m为正整数,
∴当m=4000时,W取最大值,
即药店购进A型口罩4000只、B型口罩6000只,最大利润为5600元.
第1页(共1页)
同课章节目录
