旋转对称图形课件
图片预览










文档简介
(共99张PPT)
結束
本节学习目标
1、掌握什么是旋转对称图形,会判定一个图形是不是旋转对称图形。
2、能按要求设计简单的旋转对称图形;
自学指导
自学课本P76-77内容,理解并掌握以下问题:
1.按照课本试一试的要求动手做一做。
2.理解什么叫旋转对称图形?判断一个图形是不是旋转对称图形的关键是什么?
3.思考旋转对称图形与轴对称图形有什么不同之处?
4.能否按要求设计一个旋转对称图形?
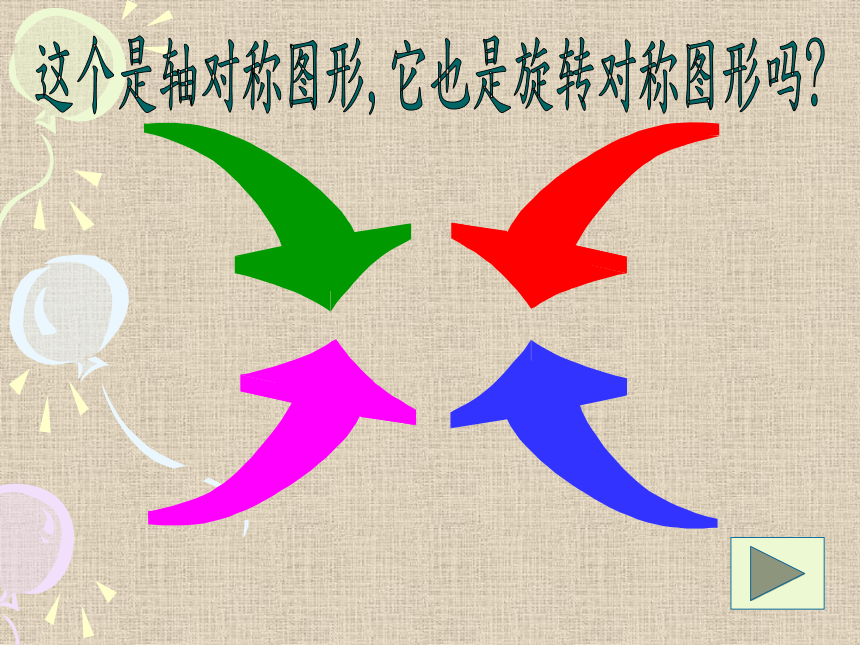
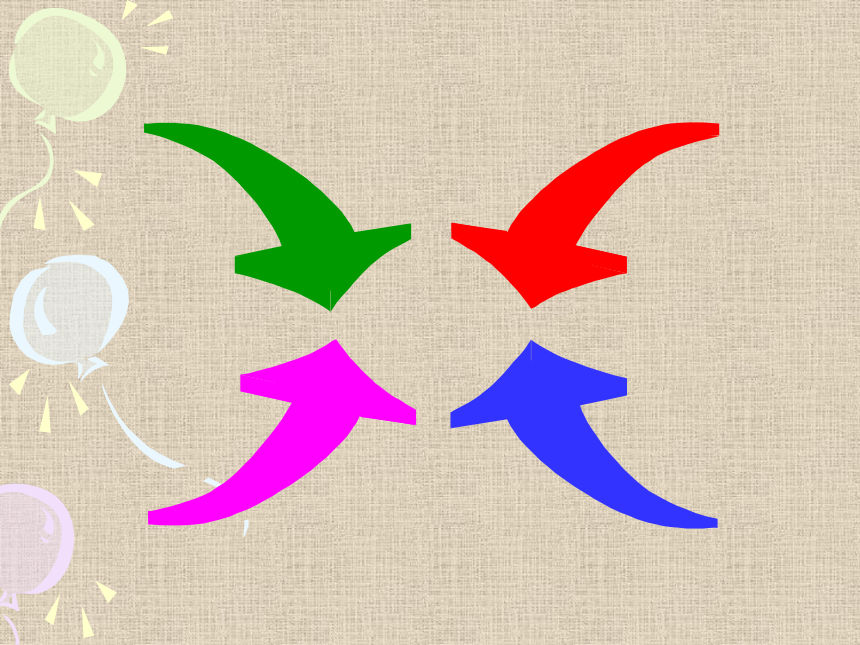
什么是旋转对称图形
一个图形在平面内绕着某一定点旋转一
定的角度(小于周角)后能与自身重合,这种
图形就称为旋转对称图形.
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合三次
旋?一周重合三次
旋?一周重合四次
旋?一周重合四次
旋?一周重合五次
旋?一周重合八次
旋?一周重合八次
旋?一周重合八次
旋?一周重合无数次
用类似上述的操作方法对如图所示的图形进行探索,看看它是不是旋转对称图形?与你的同桌找一找旋转中心在何处?该图形需要旋转多少度后,能与自身重合?该图形是不是轴对称图形?
旋转对称图形与轴对称图形是两种不同的对称图形,旋转对称图形不一定是轴对称图形,轴对称图形不一定是旋转对称图形,它们是两个不同的概念.
旋转对称图形与以前学过的轴对称图形有何关系?
一个是旋转一定的角度得到,一个是翻折得到。
2.找找看,下面图形中有几匹马? 它们的位置关系大致如何?
三 P78练习
4匹马
绕矩形两条对角线的交点旋转180度,两匹马能够分别与另两匹马大致重合,这个图形可以看作是中心对称图形
(1)将图形绕圆心旋转60,120,180,240,300度后都能与自身重合.
(2)将图形绕中心旋转90,180,270度后都能与自身重合
3.如图所示的图形绕哪一点旋转多少度后与自身重合?
1.下列英文字母中属于旋转对称图形的是( )
(A)
(B)
(C)
(D)
C
S
L
K
2.下列图形中,绕旋转中心旋转60°后能与自身重合的是( )
(A)
(B)
(C)
(D)
3.下列图形旋转180°后与愿图形一致的是( )
(A)
(B)
(C)
(D)
4.如下四个图案绕中心旋转一定角度后都能与自身重合其中有一个图案与其余三个图案 旋转的度数不同,它是( )
(A)
(B)
(C)
(D)
5.下列说法中正确的是( )
(A)是旋转对称图形,肯定不是轴对称图形;
(B) 是轴对称图形,肯定是旋转对称图形;
(C)一些图形可能既是旋转对称图形,又是轴对称图形;
(D)既不是旋转对称图形,又不是轴对称图形的图形不存在.
6.在梯形、等边三角形、等腰三角形、正方形、线段、正六边形、圆中是旋转对称图形的是_______________________________________.
等边三角形、正方形、线段、正六边形、圆
!
7.五角星至少旋转多少度后能与自身重合 ( )
(A)36°
(B) 60°
(C)72°
(D)120°
8.如右图所示,此标志图形是( )
(A)旋转对称图形;
(B)轴对称图形;
(C)既是旋转对称图形,又是轴对称图形;
(D)既不是旋转对称图形,也不是轴对称图形.
9.下列说法中正确的是( )
(A)旋转对称图形是轴对称图形;
(B) 轴对称图形是旋转对称图形;
(C)等边三角形是旋转对称图形;
(D)等边三角形的对称轴只有一条.
10.长方形的旋转中心是 ,旋转 度与自身重合;五角星旋转____________度能与自身重合.
对角线的交点
180
不止一个角度噢!
旋转作图
请你设计一个旋转90度能够重合的旋转对称图形
符合要求。
五 课堂小结
2.会找旋转对称图形的旋转中心和旋转度数;
3.旋转对称图案的设计;
4.一个图形旋转一定的角度后能与自身重合,这样的旋转角度可能不止一个.
1.什么是旋转对称图形?
课后作业
课本P79习题4、5
結束
本节学习目标
1、掌握什么是旋转对称图形,会判定一个图形是不是旋转对称图形。
2、能按要求设计简单的旋转对称图形;
自学指导
自学课本P76-77内容,理解并掌握以下问题:
1.按照课本试一试的要求动手做一做。
2.理解什么叫旋转对称图形?判断一个图形是不是旋转对称图形的关键是什么?
3.思考旋转对称图形与轴对称图形有什么不同之处?
4.能否按要求设计一个旋转对称图形?
什么是旋转对称图形
一个图形在平面内绕着某一定点旋转一
定的角度(小于周角)后能与自身重合,这种
图形就称为旋转对称图形.
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合兩次
旋?一周重合三次
旋?一周重合三次
旋?一周重合四次
旋?一周重合四次
旋?一周重合五次
旋?一周重合八次
旋?一周重合八次
旋?一周重合八次
旋?一周重合无数次
用类似上述的操作方法对如图所示的图形进行探索,看看它是不是旋转对称图形?与你的同桌找一找旋转中心在何处?该图形需要旋转多少度后,能与自身重合?该图形是不是轴对称图形?
旋转对称图形与轴对称图形是两种不同的对称图形,旋转对称图形不一定是轴对称图形,轴对称图形不一定是旋转对称图形,它们是两个不同的概念.
旋转对称图形与以前学过的轴对称图形有何关系?
一个是旋转一定的角度得到,一个是翻折得到。
2.找找看,下面图形中有几匹马? 它们的位置关系大致如何?
三 P78练习
4匹马
绕矩形两条对角线的交点旋转180度,两匹马能够分别与另两匹马大致重合,这个图形可以看作是中心对称图形
(1)将图形绕圆心旋转60,120,180,240,300度后都能与自身重合.
(2)将图形绕中心旋转90,180,270度后都能与自身重合
3.如图所示的图形绕哪一点旋转多少度后与自身重合?
1.下列英文字母中属于旋转对称图形的是( )
(A)
(B)
(C)
(D)
C
S
L
K
2.下列图形中,绕旋转中心旋转60°后能与自身重合的是( )
(A)
(B)
(C)
(D)
3.下列图形旋转180°后与愿图形一致的是( )
(A)
(B)
(C)
(D)
4.如下四个图案绕中心旋转一定角度后都能与自身重合其中有一个图案与其余三个图案 旋转的度数不同,它是( )
(A)
(B)
(C)
(D)
5.下列说法中正确的是( )
(A)是旋转对称图形,肯定不是轴对称图形;
(B) 是轴对称图形,肯定是旋转对称图形;
(C)一些图形可能既是旋转对称图形,又是轴对称图形;
(D)既不是旋转对称图形,又不是轴对称图形的图形不存在.
6.在梯形、等边三角形、等腰三角形、正方形、线段、正六边形、圆中是旋转对称图形的是_______________________________________.
等边三角形、正方形、线段、正六边形、圆
!
7.五角星至少旋转多少度后能与自身重合 ( )
(A)36°
(B) 60°
(C)72°
(D)120°
8.如右图所示,此标志图形是( )
(A)旋转对称图形;
(B)轴对称图形;
(C)既是旋转对称图形,又是轴对称图形;
(D)既不是旋转对称图形,也不是轴对称图形.
9.下列说法中正确的是( )
(A)旋转对称图形是轴对称图形;
(B) 轴对称图形是旋转对称图形;
(C)等边三角形是旋转对称图形;
(D)等边三角形的对称轴只有一条.
10.长方形的旋转中心是 ,旋转 度与自身重合;五角星旋转____________度能与自身重合.
对角线的交点
180
不止一个角度噢!
旋转作图
请你设计一个旋转90度能够重合的旋转对称图形
符合要求。
五 课堂小结
2.会找旋转对称图形的旋转中心和旋转度数;
3.旋转对称图案的设计;
4.一个图形旋转一定的角度后能与自身重合,这样的旋转角度可能不止一个.
1.什么是旋转对称图形?
课后作业
课本P79习题4、5
