禹王中学2020~2021学年第一学期高一第四次月考(word版含解析)
文档属性
| 名称 | 禹王中学2020~2021学年第一学期高一第四次月考(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 06:39:07 | ||
图片预览


文档简介
禹王中学2020~2021学年第一学期高一第四次月考
数学
本卷命题范围:北师大版必修第一册第一~五章.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.命题“?x∈R,x2+1≤1”的否定为
A.?x∈R,x2+1≥1
B.?x∈R,x2+1≥1
C.?x∈R,x2+1>1
D.?x∈R,x2+1>1
2.设集合,B={x|-4≤x≤3},则A∩B=
A.[-4,-2)∪(1,3]
B.(-2,3)
C.R
D.?
3.下列函数在(0,+∞)上为增函数的是
A.
B.f(x)=2-x
C.f(x)=ln
|x|
D.
4.函数f(x)=lg
x+x-2的零点所在区间为
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
5.已知幂函数的图象在(0,+∞)上单调递减,则a的取值范围是
A.1
B.-2
C.1或-2
D.(-2,1)
6.“x>2”是“”的
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件
7.已知t>0,则函数的最小值为
A.-2
B.
C.3
D.2
8.已知函数f(x)是定义在R上的奇函数,g(x)=f(x)+1,若g(2)=5,则g(-2)=
A.-5
B.5
C.3
D.-3
9.函数f(x)=3|x-1|的大致图象是
A.
B.
C.
D.
10.设偶函数f(x)的定义域为R,当x∈(-∞,0]时,f(x)是增函数,则,,f(π)的大小关系是
A.
B.
C.
D.
11.已知f(x)是定义域为(-∞,+∞)的奇函数,且f(1-x)=f(1+x),则f(2020)=
A.2020
B.0
C.2
D.-2019
12.已知函数若关于x的方程f(x)=a有且仅有一个实数根,则实数a的取值范围为
A.(0,1]
B.[1,+∞)
C.(-∞,1)
D.(-1,0)
二、填空题
13.函数的定义域为________.
14.已知f(x-1)=x2+1,则f(x)=________.
15.已知函数f(x)=e|x-t|+|x-t|在区间(3,+∞)上单调递增,则实数t的取值范围是__________.
16.当x>2时,函数y=4ax-1(a>0,且a≠1)的图象恒在函数y=3x-4的图象下方,则a的取值范围为________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知集合A={x|1≤2x+1≤8},B={x|(x-a)(x-a-1)<0},a∈R.
(1)若1∈B,求实数a取值范围;
(2)若“x∈B”是“x∈A”的充分不必要条件,求实数a的取值范围.
18.求下列各式的值:
(1);
(2).
19.已知函数f(x)=loga(2-2x)+loga(x+4),其中a>1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最大值为2,求a的值.
20.为保障城市蔬菜供应,某蔬菜种植基地每年投入20万元搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入2万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的经验,发现种西红柿的年收入f(x)、种黄瓜的年收入g(x)与大棚投入x分别满足,.设甲大棚的投入为a,每年两个大棚的总收入为F(a)(投入与收入的单位均为万元).
(1)求F(8)的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使年总收入F(a)最大?并求最大年总收入.
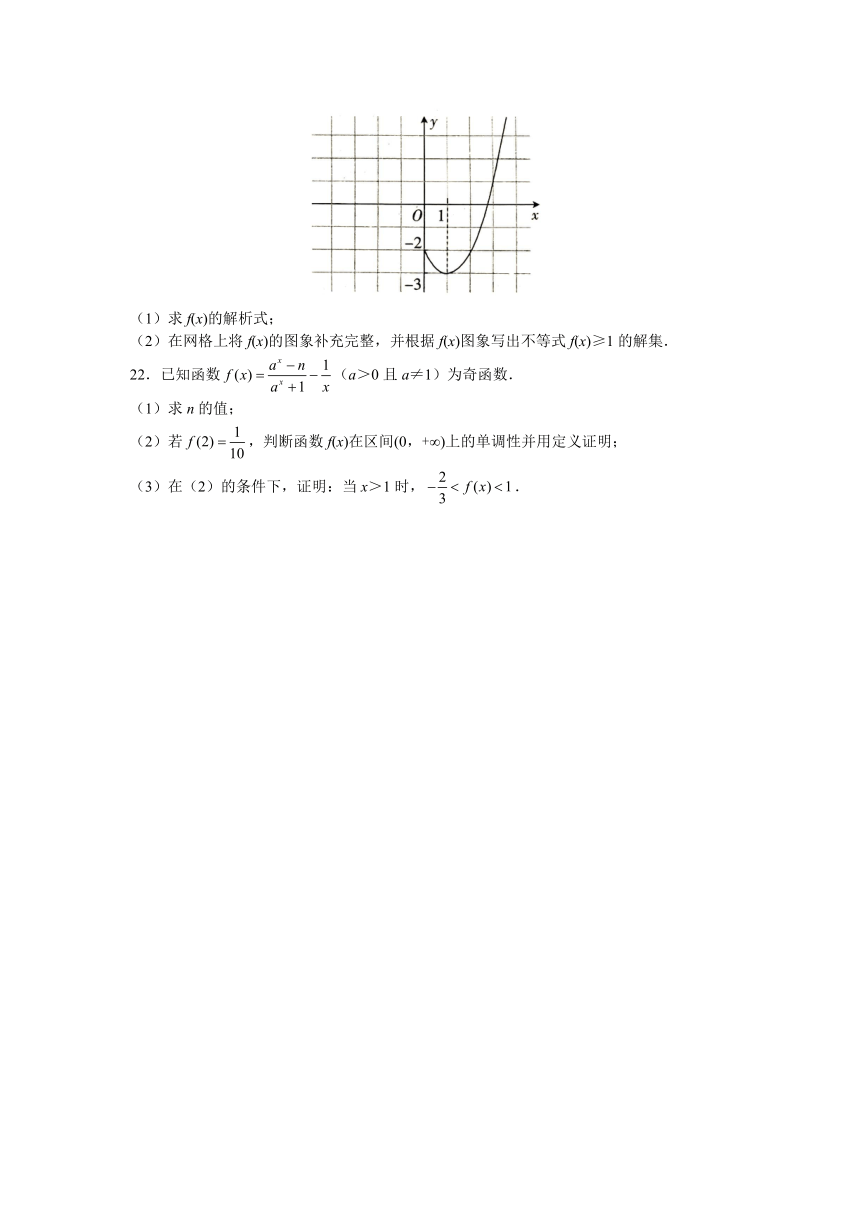
21.已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2+ax+b的部分图象如图所示.
(1)求f(x)的解析式;
(2)在网格上将f(x)的图象补充完整,并根据f(x)图象写出不等式f(x)≥1的解集.
22.已知函数(a>0且a≠1)为奇函数.
(1)求n的值;
(2)若,判断函数f(x)在区间(0,+∞)上的单调性并用定义证明;
(3)在(2)的条件下,证明:当x>1时,.
禹王中学2020~2021学年第一学期高一第四次月考·数学
参考答案、提示
1.C
“?x∈R,x2+1≤1”的否定是“?x∈R,x2+1>1”.故选C.
2.A
由,得A={x|x<-2或x>1}.又B={x|-4≤x≤3},所以A∩B=[-4,-2)∪(1,3].故选A.
3.C
函数在(0,+∞)上是减函数;在(0,+∞)上是减函数;f(x)=ln
|x|,当x>0时,f(x)=ln
x在(0,+∞)上是增函数;在(0,+∞)上是减函数.故选C.
4.B
函数f(1)=lg
1+1-2=-1<0,f(2)=lg
2+2-2=lg
2>0.又f(x)为单调增函数,所以f(x)有唯一零点,且在区间(1,2)内.故选B.
5.A
由幂函数定义得a2+a-1=1,解得a=1或a=-2.当a=1时,f(x)=x-4在(0,+∞)上单调递减;当a=-2时,f(x)=x5在(0,+∞)上单调递增.故选A.
6.A
当x>2时,得;当时,得x>1,所以“x>2”是“”的充分不必要条件.故选A.
7.C
,当且仅当,即t=1时,等号成立.故选C.
8.D
由g(2)=f(2)+1=5,则f(2)=4.因为f(x)是定义在R上的奇函数,所以f(-2)=-4,g(-2)=f(-2)+1=-4+1=-3.故选D.
9.B
函数在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增.故选B.
10.C
根据偶函数的性质可知,,当x∈[0,+∞)时,f(x)是减函数,因为,所以.故选C.
11.B
因为f(x)是定义域为(-∞,+∞)的奇函数,所以f(-x)=-f(x).因为f(1-x)=f(1+x),所以f(x+2)=f(-x),即f(x+2)=-f(x),所以f(x+4)=-f(x+2)=f(x),所以f(x)是以4为周期的函数,所以f(2020)=f(505×4+0)=f(0)=0.故选B.
12.D
作出函数f(x)的图象,由图可知,当-1<a<0时,直线y=a与f(x)的图象仅有一个交点,所以-1<a<0.故选D.
13.(0,e)
由题可得1-ln
x>0且x>0,所以0<x<e,即函数的定义域为(0,e).
14.x2+2x+2
令t=x-1,则x=t+1,f(t)=(t+1)2+1=t2+2t+2,即f(x)=x2+2x+2.
15.(-∞,3]
f(x)=e|x-t|+|x-t|.讨论:当x≥t时,f(x)=ex-t+x-t;当x≤t时,
.分析知,函数f(x)在区间[t,+∞)上单调递增,在区间(-∞,t]上单调递减.又f(x)在区间(3,+∞)上单调递增,所以3≥t.
16.
由题意,得当x>2时不等式4ax-1<3x-4恒成立,即,令f(x)=ax-1,,当a>1时,在同一平面直角坐标系中作出两个函数的图象,如图1所示,由图知不满足条件;
当0<a<1时,在同一平面直角坐标系中作出两个函数的图象,如图2所示,则f(2)≤g(2),即,解得,故a的取值范围是.
17.解:(1)若1∈B,则-a(1-a)<0,得0<a<1.
(2)由1≤2x+1≤8,得0≤x+1≤3,即-1≤x≤2,所以A={x|-1≤x≤2},B={x|(x-a)(x-a-1)<0}={x|a<x<a+1},
若“x∈B”是“x∈A”的充分不必要条件,
则B是A的真子集,
即解得-1≤a≤1,
经检验,当-1≤a≤1时均有B?A.
即实数a的取值范围是[-1,1].
18.解:(1)原式.
(2)原式.
19.解:(1)要使函数有意义,则有
解得-4<x<1,
所以函数f(x)的定义域为(-4,1).
(2)函数可化为
,
因为-4<x<1,所以.
因为a>1,所以
,
即,
由,解得.
20.解:(1)由题意知,
所以
(万元).
(2)依题意得解得2≤a≤18,
故.
令,则,,
显然在区间
上G(t)单调递增,
所以当,即a=18时,F(a)取得最大值,F(a)max=44.5,
所以当甲大棚投入18万元,乙大棚投入2万元时,年总收入最大,且最大年总收入为44.5万元.
21.解:(1)由题意得,解得,
则当x≥0时,f(x)=x2-2x-2.
因为f(x)是定义在R上的偶函数,
所以当x<0时,f(x)=f(-x)=(-x)2-2(-x)-2=x2+2x-2.
故.
(2)
由f(x)的图象可得,不等式f(x)≥1的解集为(-∞,-3]∪[3,+∞).
22.(1)解:因为是定义域为(-∞,0)∪(0,+∞)的奇函数,
所以f(-1)+f(1)=0,即,
整理得,因为a>0,
所以n=1.
经检验,当n=1时(a>0且a≠1)为奇函数,故所求n的值为1.
(2)函数f(x)在(0,+∞)上单调递增,
证明:由,得a=2,
任取x1,x2∈(0,+∞)且x1<x2,
则.
因为x2>x1>0,所以x1-x2<0,,,所以,
则,
所以f(x1)-f(x2)<0,f(x1)<f(x2),
所以f(x)在(0,+∞)上是单调递增的.
(3)证明:由(2)知,f(x)在(1,+∞)上是单调递增的,
当x>1时,f(x)>f(1),
又,从而,
又,
而当x>1时,,,所以f(x)<1,
综上,当x>1时,.
数学
本卷命题范围:北师大版必修第一册第一~五章.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.命题“?x∈R,x2+1≤1”的否定为
A.?x∈R,x2+1≥1
B.?x∈R,x2+1≥1
C.?x∈R,x2+1>1
D.?x∈R,x2+1>1
2.设集合,B={x|-4≤x≤3},则A∩B=
A.[-4,-2)∪(1,3]
B.(-2,3)
C.R
D.?
3.下列函数在(0,+∞)上为增函数的是
A.
B.f(x)=2-x
C.f(x)=ln
|x|
D.
4.函数f(x)=lg
x+x-2的零点所在区间为
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
5.已知幂函数的图象在(0,+∞)上单调递减,则a的取值范围是
A.1
B.-2
C.1或-2
D.(-2,1)
6.“x>2”是“”的
A.充分不必要条件
B.充要条件
C.必要不充分条件
D.既不充分也不必要条件
7.已知t>0,则函数的最小值为
A.-2
B.
C.3
D.2
8.已知函数f(x)是定义在R上的奇函数,g(x)=f(x)+1,若g(2)=5,则g(-2)=
A.-5
B.5
C.3
D.-3
9.函数f(x)=3|x-1|的大致图象是
A.
B.
C.
D.
10.设偶函数f(x)的定义域为R,当x∈(-∞,0]时,f(x)是增函数,则,,f(π)的大小关系是
A.
B.
C.
D.
11.已知f(x)是定义域为(-∞,+∞)的奇函数,且f(1-x)=f(1+x),则f(2020)=
A.2020
B.0
C.2
D.-2019
12.已知函数若关于x的方程f(x)=a有且仅有一个实数根,则实数a的取值范围为
A.(0,1]
B.[1,+∞)
C.(-∞,1)
D.(-1,0)
二、填空题
13.函数的定义域为________.
14.已知f(x-1)=x2+1,则f(x)=________.
15.已知函数f(x)=e|x-t|+|x-t|在区间(3,+∞)上单调递增,则实数t的取值范围是__________.
16.当x>2时,函数y=4ax-1(a>0,且a≠1)的图象恒在函数y=3x-4的图象下方,则a的取值范围为________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知集合A={x|1≤2x+1≤8},B={x|(x-a)(x-a-1)<0},a∈R.
(1)若1∈B,求实数a取值范围;
(2)若“x∈B”是“x∈A”的充分不必要条件,求实数a的取值范围.
18.求下列各式的值:
(1);
(2).
19.已知函数f(x)=loga(2-2x)+loga(x+4),其中a>1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最大值为2,求a的值.
20.为保障城市蔬菜供应,某蔬菜种植基地每年投入20万元搭建甲、乙两个无公害蔬菜大棚,每个大棚至少要投入2万元,其中甲大棚种西红柿,乙大棚种黄瓜.根据以往的经验,发现种西红柿的年收入f(x)、种黄瓜的年收入g(x)与大棚投入x分别满足,.设甲大棚的投入为a,每年两个大棚的总收入为F(a)(投入与收入的单位均为万元).
(1)求F(8)的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使年总收入F(a)最大?并求最大年总收入.
21.已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2+ax+b的部分图象如图所示.
(1)求f(x)的解析式;
(2)在网格上将f(x)的图象补充完整,并根据f(x)图象写出不等式f(x)≥1的解集.
22.已知函数(a>0且a≠1)为奇函数.
(1)求n的值;
(2)若,判断函数f(x)在区间(0,+∞)上的单调性并用定义证明;
(3)在(2)的条件下,证明:当x>1时,.
禹王中学2020~2021学年第一学期高一第四次月考·数学
参考答案、提示
1.C
“?x∈R,x2+1≤1”的否定是“?x∈R,x2+1>1”.故选C.
2.A
由,得A={x|x<-2或x>1}.又B={x|-4≤x≤3},所以A∩B=[-4,-2)∪(1,3].故选A.
3.C
函数在(0,+∞)上是减函数;在(0,+∞)上是减函数;f(x)=ln
|x|,当x>0时,f(x)=ln
x在(0,+∞)上是增函数;在(0,+∞)上是减函数.故选C.
4.B
函数f(1)=lg
1+1-2=-1<0,f(2)=lg
2+2-2=lg
2>0.又f(x)为单调增函数,所以f(x)有唯一零点,且在区间(1,2)内.故选B.
5.A
由幂函数定义得a2+a-1=1,解得a=1或a=-2.当a=1时,f(x)=x-4在(0,+∞)上单调递减;当a=-2时,f(x)=x5在(0,+∞)上单调递增.故选A.
6.A
当x>2时,得;当时,得x>1,所以“x>2”是“”的充分不必要条件.故选A.
7.C
,当且仅当,即t=1时,等号成立.故选C.
8.D
由g(2)=f(2)+1=5,则f(2)=4.因为f(x)是定义在R上的奇函数,所以f(-2)=-4,g(-2)=f(-2)+1=-4+1=-3.故选D.
9.B
函数在区间(-∞,1)上单调递减,在区间(1,+∞)上单调递增.故选B.
10.C
根据偶函数的性质可知,,当x∈[0,+∞)时,f(x)是减函数,因为,所以.故选C.
11.B
因为f(x)是定义域为(-∞,+∞)的奇函数,所以f(-x)=-f(x).因为f(1-x)=f(1+x),所以f(x+2)=f(-x),即f(x+2)=-f(x),所以f(x+4)=-f(x+2)=f(x),所以f(x)是以4为周期的函数,所以f(2020)=f(505×4+0)=f(0)=0.故选B.
12.D
作出函数f(x)的图象,由图可知,当-1<a<0时,直线y=a与f(x)的图象仅有一个交点,所以-1<a<0.故选D.
13.(0,e)
由题可得1-ln
x>0且x>0,所以0<x<e,即函数的定义域为(0,e).
14.x2+2x+2
令t=x-1,则x=t+1,f(t)=(t+1)2+1=t2+2t+2,即f(x)=x2+2x+2.
15.(-∞,3]
f(x)=e|x-t|+|x-t|.讨论:当x≥t时,f(x)=ex-t+x-t;当x≤t时,
.分析知,函数f(x)在区间[t,+∞)上单调递增,在区间(-∞,t]上单调递减.又f(x)在区间(3,+∞)上单调递增,所以3≥t.
16.
由题意,得当x>2时不等式4ax-1<3x-4恒成立,即,令f(x)=ax-1,,当a>1时,在同一平面直角坐标系中作出两个函数的图象,如图1所示,由图知不满足条件;
当0<a<1时,在同一平面直角坐标系中作出两个函数的图象,如图2所示,则f(2)≤g(2),即,解得,故a的取值范围是.
17.解:(1)若1∈B,则-a(1-a)<0,得0<a<1.
(2)由1≤2x+1≤8,得0≤x+1≤3,即-1≤x≤2,所以A={x|-1≤x≤2},B={x|(x-a)(x-a-1)<0}={x|a<x<a+1},
若“x∈B”是“x∈A”的充分不必要条件,
则B是A的真子集,
即解得-1≤a≤1,
经检验,当-1≤a≤1时均有B?A.
即实数a的取值范围是[-1,1].
18.解:(1)原式.
(2)原式.
19.解:(1)要使函数有意义,则有
解得-4<x<1,
所以函数f(x)的定义域为(-4,1).
(2)函数可化为
,
因为-4<x<1,所以.
因为a>1,所以
,
即,
由,解得.
20.解:(1)由题意知,
所以
(万元).
(2)依题意得解得2≤a≤18,
故.
令,则,,
显然在区间
上G(t)单调递增,
所以当,即a=18时,F(a)取得最大值,F(a)max=44.5,
所以当甲大棚投入18万元,乙大棚投入2万元时,年总收入最大,且最大年总收入为44.5万元.
21.解:(1)由题意得,解得,
则当x≥0时,f(x)=x2-2x-2.
因为f(x)是定义在R上的偶函数,
所以当x<0时,f(x)=f(-x)=(-x)2-2(-x)-2=x2+2x-2.
故.
(2)
由f(x)的图象可得,不等式f(x)≥1的解集为(-∞,-3]∪[3,+∞).
22.(1)解:因为是定义域为(-∞,0)∪(0,+∞)的奇函数,
所以f(-1)+f(1)=0,即,
整理得,因为a>0,
所以n=1.
经检验,当n=1时(a>0且a≠1)为奇函数,故所求n的值为1.
(2)函数f(x)在(0,+∞)上单调递增,
证明:由,得a=2,
任取x1,x2∈(0,+∞)且x1<x2,
则.
因为x2>x1>0,所以x1-x2<0,,,所以,
则,
所以f(x1)-f(x2)<0,f(x1)<f(x2),
所以f(x)在(0,+∞)上是单调递增的.
(3)证明:由(2)知,f(x)在(1,+∞)上是单调递增的,
当x>1时,f(x)>f(1),
又,从而,
又,
而当x>1时,,,所以f(x)<1,
综上,当x>1时,.
