小学数学青岛版六三制四年级上册八 新校服—— 植树问题(27张PPT)
文档属性
| 名称 | 小学数学青岛版六三制四年级上册八 新校服—— 植树问题(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 19:29:19 | ||
图片预览







文档简介
(共27张PPT)
植树问题
刘山山
智慧广场
创设情境
猜谜语:
两棵小树十个叉,不长叶子不开花。
能写会算还会画,天天干活不说话。
(打一身体器官)
5个手指有几个空?
间隔
5个手指有4个间隔。
在数学上,我们把像这样的空叫做间隔。
教学目标
1.通过动手操作的实践活动,探索并发现间隔数与植树棵数之间的关系。
2.通过小组合作、交流,理解间隔数与植树棵数之间的规律。
3.能够借助图形,利用规律来解决简单植树问题。
情境导入
说一说,你知道了什么?
你能提出什么数学问题呢?
学校门前有一条长50米的小路,计划在小路一旁植树,每5米栽一棵。
合作探索
两端都栽,需要多少棵树苗?
我先画图看一看。
5米
50米
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
平均分成10段,要栽11棵。
两端都栽,需要多少棵树苗?
我是这样算的……
间隔
5棵树之间有4个间距。
50
÷
5
+
1
=
11(棵)
间隔数
+
1
=
棵数
用手指代表树,用两指间的空隙代表树间隔。
间隔数
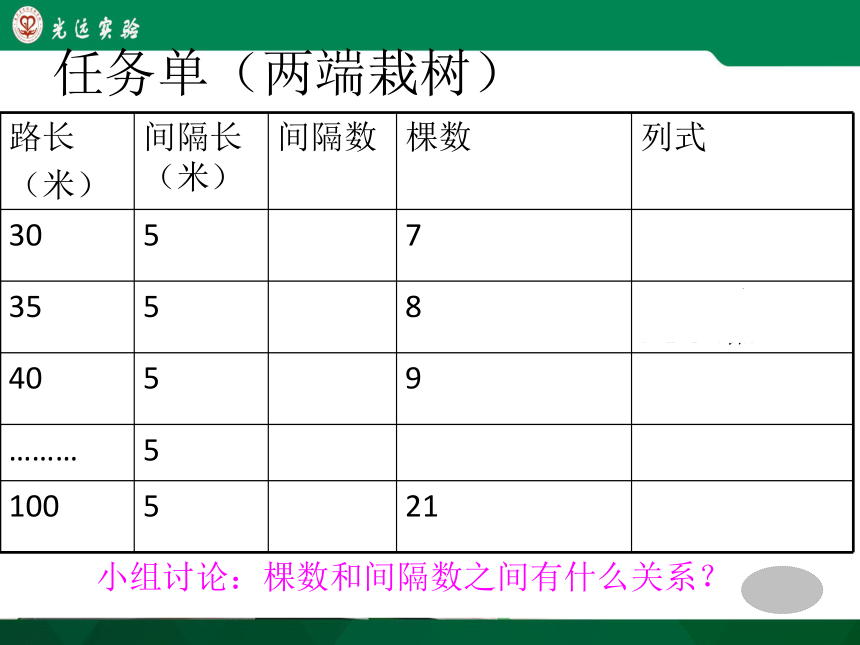
任务单(两端栽树)
路长
(米)
间隔长(米)
间隔数
棵数
列式
30
5
6
7
30÷5=6(个)
6+1=7(棵)
35
5
7
8
35÷5=7(个)
7+1=8(棵)
40
5
8
9
40÷5=8(个)
8+1=9(棵)
………
5
100
5
20
21
100÷5=20(个)
20+1=21(棵)
小组讨论:棵数和间隔数之间有什么关系?
建立数学模型
一边植树
两端都栽
棵数=间隔数+1
间隔数=总长÷间隔长
在一条全长180米的街道一旁安装路灯,(两端都要安装),每隔6米安一座。一共要安装多少座路灯?
间隔数:180
÷
6
=
30(个)
路灯数:30
+
1
=
31(座)
答:一共要安装
31
座路灯。
合作探究
同学们在全长100米的小路一边植树,每隔5米栽一棵树(只栽一端),一共要栽多少棵树?
如果一端不栽,需要多少棵树苗呢?
我用画图法解答。
5米
50米
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
平均分成10段,要栽10棵。
如果一端不栽,需要多少棵树苗呢?
还可以这样算……
握住大拇指,数一数。
间隔数
=
棵数
50
÷
5
=
10(棵)
任务单(一端栽树)
路长
(米)
间隔数(米)
间隔数
棵数
列式
30
5
6
6
30÷5=6(棵)
35
5
7
7
35÷5=7(棵)
40
5
8
8
40÷5=8(棵)
………
5
100
5
20
20
100÷5=20(棵)
你的发现:一端栽树棵树=间隔数
建立数学模型
一边植树
只栽一端
棵数=间隔数
间隔数=总长÷间隔长
同学们在全长100米的小路一边植树,每隔5米栽一棵树(两端不栽),一共要栽多少棵树?
如果两端不栽,需要多少棵树苗呢?
还是可以画图解决。
5米
50米
1
2
3
4
5
6
7
8
9
10
平均分成10段,要栽9棵。
如果两端不栽,需要多少棵树苗呢?
也可以借助手来计算。
握住大拇指和小拇指,数一数。
50
÷
5
-
1
=
9(棵)
间隔数
–
1
=
棵数
建立数学模型
一边植树
只栽一端
棵数=间隔数
间隔数=总长÷间隔长
想一想,植树问题有什么规律呢?
两端都栽:
一端不栽:
两端都不栽:
间隔数
+
1
=
棵数
间隔数
=
棵数
间隔数
-1
=
棵数
在现实生活中的“植树问题”,题目里一定要存在真实的“树”吗?
除了真实的“树”,还能换成别的事物吗?
深入思考,举一反三
斑马线
楼道版面
楼层
马路两边的树
公示栏
乒乓球台…
这里又把(
)看成了树?
我们每天中午吃饭时食堂的凳子整齐地排在一起
1.一条走廊长32米,每隔4米放一盆花,两端都要放,
一共需要放多少盆花?
间隔数:32
÷
4
=
8(个)
花盆数:8
+
1
=
9(盆)
答:一共需要放
9
盆花。
我能行!
2.
把一根木头锯成5段,每锯断一次需要6分钟,锯完这根木头一共需要多少分钟?(先画出示意图,再列式解答)
5
–
1
=
4(次)
4
×
6
=
24(分)
答:一共需要
24
分钟。
3.下面哪条算式是正确的?
一列共有25张凳子,有(
)个间隔。
①25+1=26个
②25个
③25-1=24个
课堂小结
通过今天的学习你有什么收获?
植树问题
刘山山
智慧广场
创设情境
猜谜语:
两棵小树十个叉,不长叶子不开花。
能写会算还会画,天天干活不说话。
(打一身体器官)
5个手指有几个空?
间隔
5个手指有4个间隔。
在数学上,我们把像这样的空叫做间隔。
教学目标
1.通过动手操作的实践活动,探索并发现间隔数与植树棵数之间的关系。
2.通过小组合作、交流,理解间隔数与植树棵数之间的规律。
3.能够借助图形,利用规律来解决简单植树问题。
情境导入
说一说,你知道了什么?
你能提出什么数学问题呢?
学校门前有一条长50米的小路,计划在小路一旁植树,每5米栽一棵。
合作探索
两端都栽,需要多少棵树苗?
我先画图看一看。
5米
50米
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
11
平均分成10段,要栽11棵。
两端都栽,需要多少棵树苗?
我是这样算的……
间隔
5棵树之间有4个间距。
50
÷
5
+
1
=
11(棵)
间隔数
+
1
=
棵数
用手指代表树,用两指间的空隙代表树间隔。
间隔数
任务单(两端栽树)
路长
(米)
间隔长(米)
间隔数
棵数
列式
30
5
6
7
30÷5=6(个)
6+1=7(棵)
35
5
7
8
35÷5=7(个)
7+1=8(棵)
40
5
8
9
40÷5=8(个)
8+1=9(棵)
………
5
100
5
20
21
100÷5=20(个)
20+1=21(棵)
小组讨论:棵数和间隔数之间有什么关系?
建立数学模型
一边植树
两端都栽
棵数=间隔数+1
间隔数=总长÷间隔长
在一条全长180米的街道一旁安装路灯,(两端都要安装),每隔6米安一座。一共要安装多少座路灯?
间隔数:180
÷
6
=
30(个)
路灯数:30
+
1
=
31(座)
答:一共要安装
31
座路灯。
合作探究
同学们在全长100米的小路一边植树,每隔5米栽一棵树(只栽一端),一共要栽多少棵树?
如果一端不栽,需要多少棵树苗呢?
我用画图法解答。
5米
50米
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
平均分成10段,要栽10棵。
如果一端不栽,需要多少棵树苗呢?
还可以这样算……
握住大拇指,数一数。
间隔数
=
棵数
50
÷
5
=
10(棵)
任务单(一端栽树)
路长
(米)
间隔数(米)
间隔数
棵数
列式
30
5
6
6
30÷5=6(棵)
35
5
7
7
35÷5=7(棵)
40
5
8
8
40÷5=8(棵)
………
5
100
5
20
20
100÷5=20(棵)
你的发现:一端栽树棵树=间隔数
建立数学模型
一边植树
只栽一端
棵数=间隔数
间隔数=总长÷间隔长
同学们在全长100米的小路一边植树,每隔5米栽一棵树(两端不栽),一共要栽多少棵树?
如果两端不栽,需要多少棵树苗呢?
还是可以画图解决。
5米
50米
1
2
3
4
5
6
7
8
9
10
平均分成10段,要栽9棵。
如果两端不栽,需要多少棵树苗呢?
也可以借助手来计算。
握住大拇指和小拇指,数一数。
50
÷
5
-
1
=
9(棵)
间隔数
–
1
=
棵数
建立数学模型
一边植树
只栽一端
棵数=间隔数
间隔数=总长÷间隔长
想一想,植树问题有什么规律呢?
两端都栽:
一端不栽:
两端都不栽:
间隔数
+
1
=
棵数
间隔数
=
棵数
间隔数
-1
=
棵数
在现实生活中的“植树问题”,题目里一定要存在真实的“树”吗?
除了真实的“树”,还能换成别的事物吗?
深入思考,举一反三
斑马线
楼道版面
楼层
马路两边的树
公示栏
乒乓球台…
这里又把(
)看成了树?
我们每天中午吃饭时食堂的凳子整齐地排在一起
1.一条走廊长32米,每隔4米放一盆花,两端都要放,
一共需要放多少盆花?
间隔数:32
÷
4
=
8(个)
花盆数:8
+
1
=
9(盆)
答:一共需要放
9
盆花。
我能行!
2.
把一根木头锯成5段,每锯断一次需要6分钟,锯完这根木头一共需要多少分钟?(先画出示意图,再列式解答)
5
–
1
=
4(次)
4
×
6
=
24(分)
答:一共需要
24
分钟。
3.下面哪条算式是正确的?
一列共有25张凳子,有(
)个间隔。
①25+1=26个
②25个
③25-1=24个
课堂小结
通过今天的学习你有什么收获?
