29.3 课题学习制作立体模型(共18张ppt)
文档属性
| 名称 | 29.3 课题学习制作立体模型(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 15:42:09 | ||
图片预览




文档简介
(共18张PPT)
29.3
课题学习
制作立体模型
人教版·九年级数学·下册
1.理解三种视图所表示的意思以及视图间的联系.
2.经历根据三视图制作立体模型的过程.
3.感受立体图形与平面图形之间的联系.
重点:通过根据三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图表之间的联系..
难点:应用数学知识解决问题的意识和能力.
阅读课本P105-106页内容,
了解本节主要内容.
立体图形
三视图
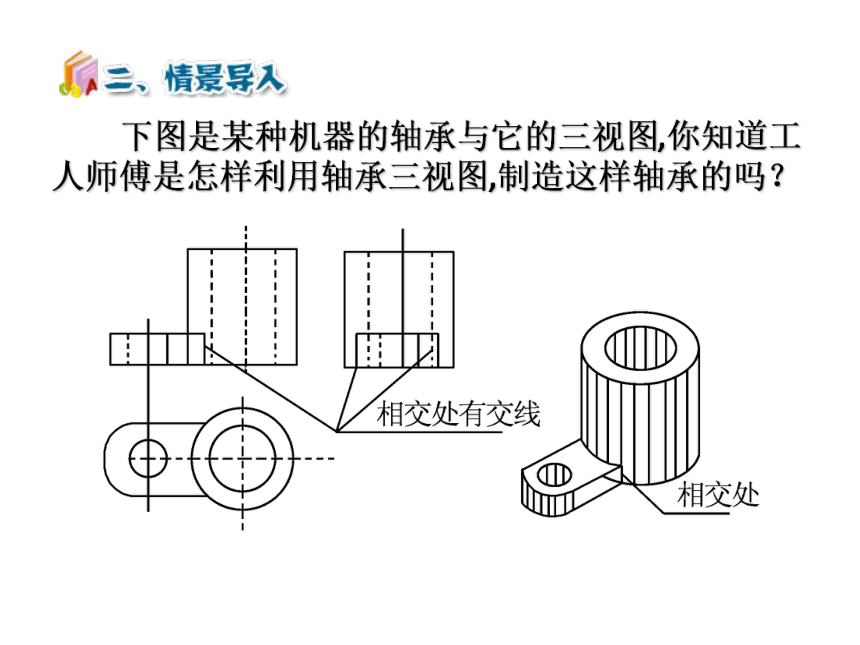
下图是某种机器的轴承与它的三视图,你知道工人师傅是怎样利用轴承三视图,制造这样轴承的吗?
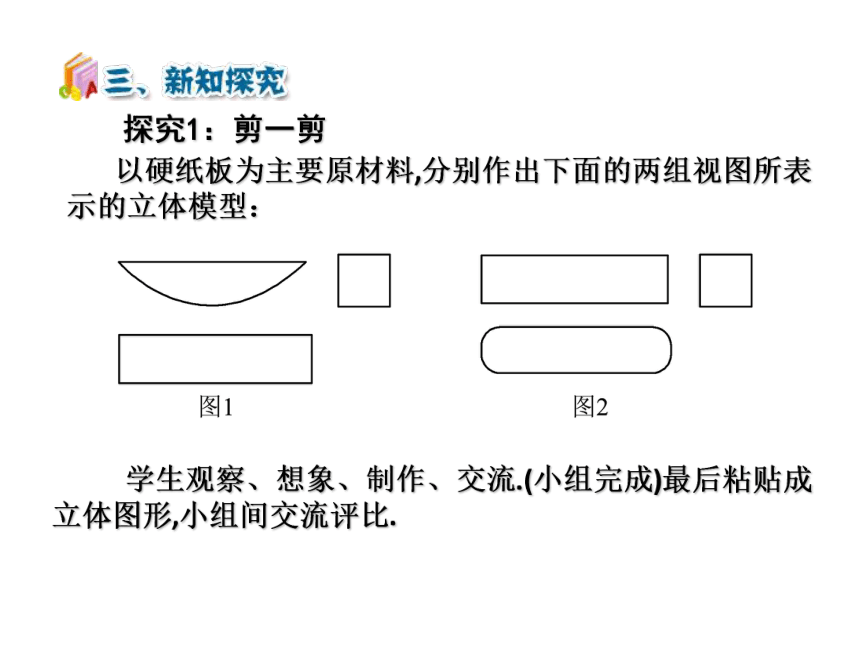
探究1:剪一剪
以硬纸板为主要原材料,分别作出下面的两组视图所表示的立体模型:
学生观察、想象、制作、交流.(小组完成)最后粘贴成立体图形,小组间交流评比.
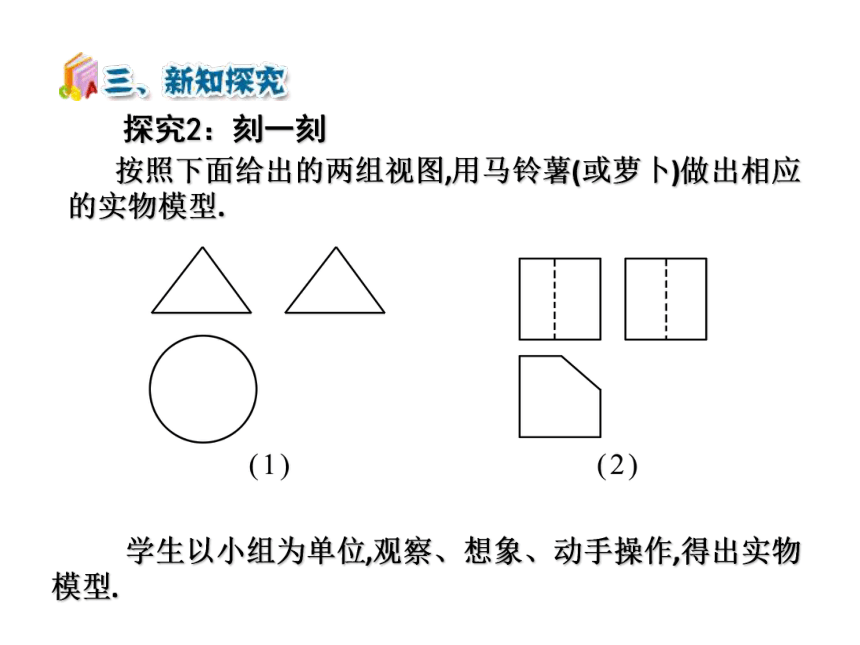
探究2:刻一刻
按照下面给出的两组视图,用马铃薯(或萝卜)做出相应的实物模型.
学生以小组为单位,观察、想象、动手操作,得出实物模型.
探究3:写一写
三视图和展开图都是与立体图形有关的平面图形,了解有关生产实际,结合具体例子,写一篇短文介绍三视图、展开图的应用.
200
D
B
例1:如图所示,每一组的平面图形都是由四个等边三角形组成的.
解析:
(1)
如图所示,只有图①③能折叠成四面体,图②中使a、b边重合,四个三角形组成一个几何体侧面,而底面是空的;
解:
(1)图①能折叠成一个正四面体,四面体模型如图(a)所示;
(1)指出其中哪些可以折叠成多面体,把三个图形描在纸上,剪下来,叠一叠,验证你的答案;
例1:如图所示,每一组的平面图形都是由四个等边三角形组成的.
解析:
(2)由三视图可确定物体放置位置,由物体具体位置才能画其三视图;
解:
(2)该四面体是正三棱锥,正三棱锥的三视图如图(b)所示,主视图长与俯视图长对正,主视图高与左视图高平齐,俯视图宽与左视图宽相等;
(2)画出由图中的图形能折叠成的多面体的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的;
例1:如图所示,每一组的平面图形都是由四个等边三角形组成的.
解析:
(3)四面体的体积运用三棱锥体积公式V=
Sh求解,表面
积为4个等边三角形面积的和.
解:
(3)如图(c)所示,过A作AO⊥面BCD,过O作OE⊥CD于E,
(3)如果图中小三角形的边长为1,那么对应的几何体的体积和表面积是多少?(三棱锥体积V=
Sh)
6
D
A
解:
由三视图可知,密封罐的形状是正六棱柱.
密封罐的高为5cm,底面正六边形的直径为10cm,边长为5cm,
由展开可知,制作一个纸盒所需纸板面积为:
由三视图制作立体模型的思路过程是:三视图→立体图形→展开图→制作模型.
29.3
课题学习
制作立体模型
人教版·九年级数学·下册
1.理解三种视图所表示的意思以及视图间的联系.
2.经历根据三视图制作立体模型的过程.
3.感受立体图形与平面图形之间的联系.
重点:通过根据三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会用三视图表示立体图形的作用,进一步感受立体图形与平面图表之间的联系..
难点:应用数学知识解决问题的意识和能力.
阅读课本P105-106页内容,
了解本节主要内容.
立体图形
三视图
下图是某种机器的轴承与它的三视图,你知道工人师傅是怎样利用轴承三视图,制造这样轴承的吗?
探究1:剪一剪
以硬纸板为主要原材料,分别作出下面的两组视图所表示的立体模型:
学生观察、想象、制作、交流.(小组完成)最后粘贴成立体图形,小组间交流评比.
探究2:刻一刻
按照下面给出的两组视图,用马铃薯(或萝卜)做出相应的实物模型.
学生以小组为单位,观察、想象、动手操作,得出实物模型.
探究3:写一写
三视图和展开图都是与立体图形有关的平面图形,了解有关生产实际,结合具体例子,写一篇短文介绍三视图、展开图的应用.
200
D
B
例1:如图所示,每一组的平面图形都是由四个等边三角形组成的.
解析:
(1)
如图所示,只有图①③能折叠成四面体,图②中使a、b边重合,四个三角形组成一个几何体侧面,而底面是空的;
解:
(1)图①能折叠成一个正四面体,四面体模型如图(a)所示;
(1)指出其中哪些可以折叠成多面体,把三个图形描在纸上,剪下来,叠一叠,验证你的答案;
例1:如图所示,每一组的平面图形都是由四个等边三角形组成的.
解析:
(2)由三视图可确定物体放置位置,由物体具体位置才能画其三视图;
解:
(2)该四面体是正三棱锥,正三棱锥的三视图如图(b)所示,主视图长与俯视图长对正,主视图高与左视图高平齐,俯视图宽与左视图宽相等;
(2)画出由图中的图形能折叠成的多面体的三视图,并指出三视图中是怎样体现“长对正,高平齐,宽相等”的;
例1:如图所示,每一组的平面图形都是由四个等边三角形组成的.
解析:
(3)四面体的体积运用三棱锥体积公式V=
Sh求解,表面
积为4个等边三角形面积的和.
解:
(3)如图(c)所示,过A作AO⊥面BCD,过O作OE⊥CD于E,
(3)如果图中小三角形的边长为1,那么对应的几何体的体积和表面积是多少?(三棱锥体积V=
Sh)
6
D
A
解:
由三视图可知,密封罐的形状是正六棱柱.
密封罐的高为5cm,底面正六边形的直径为10cm,边长为5cm,
由展开可知,制作一个纸盒所需纸板面积为:
由三视图制作立体模型的思路过程是:三视图→立体图形→展开图→制作模型.
