人教版数学九年级下册数学:第27章 相似 专题练习(word版附答案)
文档属性
| 名称 | 人教版数学九年级下册数学:第27章 相似 专题练习(word版附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 328.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览



文档简介
专题1 相似三角形的基本模型
模型1 A字型及其变形
(1)如图1,公共角所对的边平行(DE∥BC),则△ADE∽△ABC;
(2)如图2,公共角的对边不平行,且有另一组角相等(∠AED=∠ABC或∠ADE=∠ACB),则△AED∽△ABC.
【例1】 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,求AD·BC的值.
42989500解:∵∠ADE=∠B,∠EAD=∠CAB,
∴△ADE∽△ABC.
∴=.
∴AD·BC=DE·AB.
又∵DE=2,AB=5,
∴AD·BC=2×5=10.
1.如图,在△ABC中,DE∥BC,DF∥AC,AE=3,AC=5,BC=10,则BF的长为 .
2.如图,在锐角△ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.求证:△ADE∽△ABC.
模型2 X字型及其变形
(1)如图1,对顶角的对边平行(AB∥CD),则△ABO∽△DCO;
(2)如图2,对顶角的对边不平行,且有另一对角相等(∠B=∠D或∠A=∠C),则△ABO∽△CDO.
【例2】 如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.求证:△ABO∽△CDO.
41313100证明:∵AB∥CD,
∴∠OAB=∠OCD,
∠OBA=∠ODC.
∴△ABO∽△CDO.
【补充设问】△AOD与△BOC相似吗?试说明理由.
解:△AOD与△BOC不相似.
理由如下:∵∠AOD=∠COB,
要使△AOD与△BOC相似,
∴当满足=或=时,
即DO·BO=AO·CO或DO·CO=AO·BO时,△AOD与△BOC相似.
由已证可知△ABO∽△CDO,∴=,
即AO·DO=BO·CO,不满足证明△AOD与△BOC相似的条件.
∴△AOD与△BOC不相似.
【变式】 如图,在四边形ABDC中,若AB不平行于CD,∠ABC=∠ADC,则图中的相似三角形有△COD∽△AOB,△AOC∽△BOD.
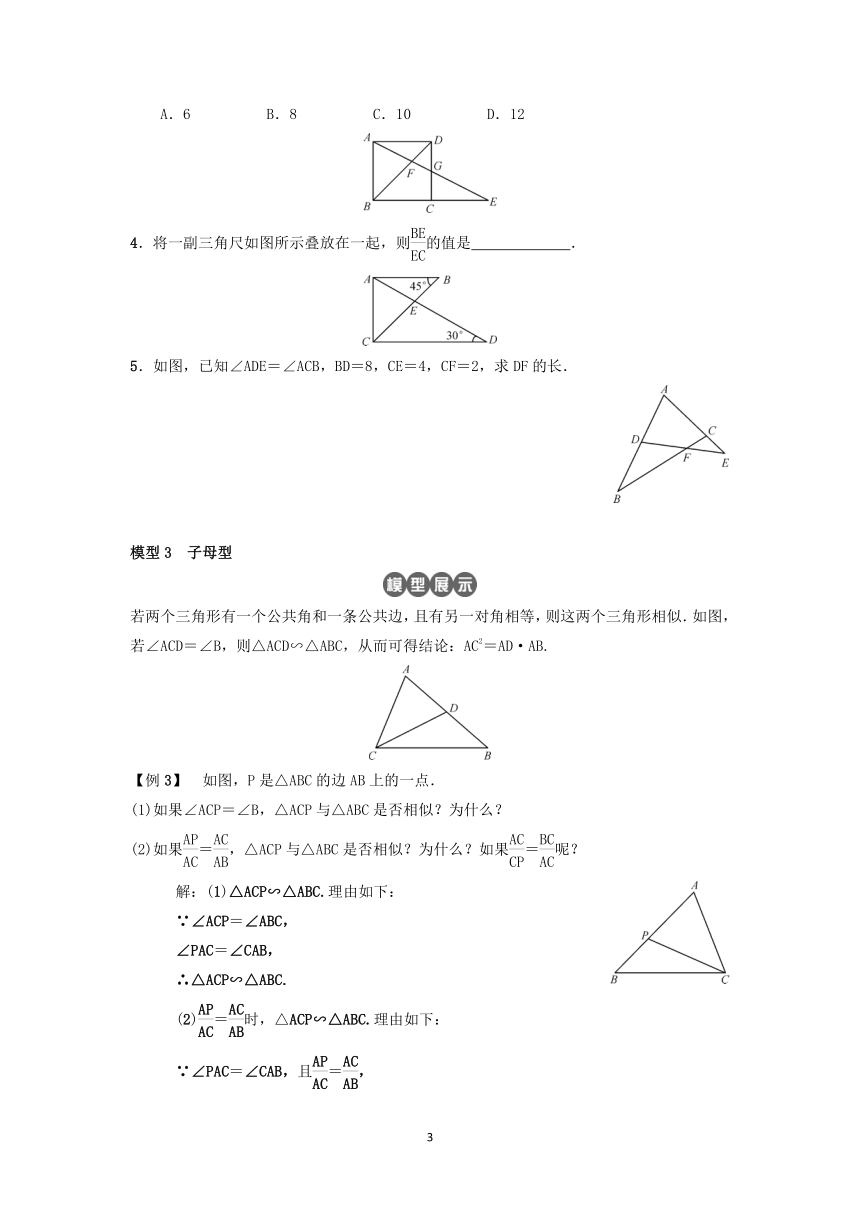
3.如图,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F,已知FG=2,则线段AE的长度为( )
A.6 B.8 C.10 D.12
4.将一副三角尺如图所示叠放在一起,则的值是 .
5.如图,已知∠ADE=∠ACB,BD=8,CE=4,CF=2,求DF的长.
模型3 子母型
若两个三角形有一个公共角和一条公共边,且有另一对角相等,则这两个三角形相似.如图,若∠ACD=∠B,则△ACD∽△ABC,从而可得结论:AC2=AD·AB.
【例3】 如图,P是△ABC的边AB上的一点.
(1)如果∠ACP=∠B,△ACP与△ABC是否相似?为什么?
(2)如果=,△ACP与△ABC是否相似?为什么?如果=呢?
42227500解:(1)△ACP∽△ABC.理由如下:
∵∠ACP=∠ABC,
∠PAC=∠CAB,
∴△ACP∽△ABC.
(2)=时,△ACP∽△ABC.理由如下:
∵∠PAC=∠CAB,且=,
∴△ACP∽△ABC.
由=不能得到△ACP与△ABC相似.
∵AC与CP的夹角为∠ACP,BC与AC的夹角为∠ACB,
而∠ACP与∠ACB不相等,
∴由=不能得到△ACP与△ABC相似.
6.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
7.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,若BC=2,AB=3,则BD的长为 .
模型4 双垂直型
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.如图,Rt△ABC中,CD为斜边AB上的高,则有△ACD∽△ABC∽△CBD,从而可得结论:CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.
【例4】 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出AD2=BD·DC吗?41313100
解:(1)△BAD∽△BCA∽△ACD.
(2)能得出AD2=BD·DC.
理由如下:
∵∠BAC=90°,
∴∠BAD+∠DAC=90°.
∵AD⊥BC,
∴∠DAC+∠ACD=90°,∠BDA=∠ADC=90°.
∴∠BAD=∠ACD.
又∵∠BDA=∠ADC,
∴△BAD∽△ACD.
∴=,即AD2=BD·DC.
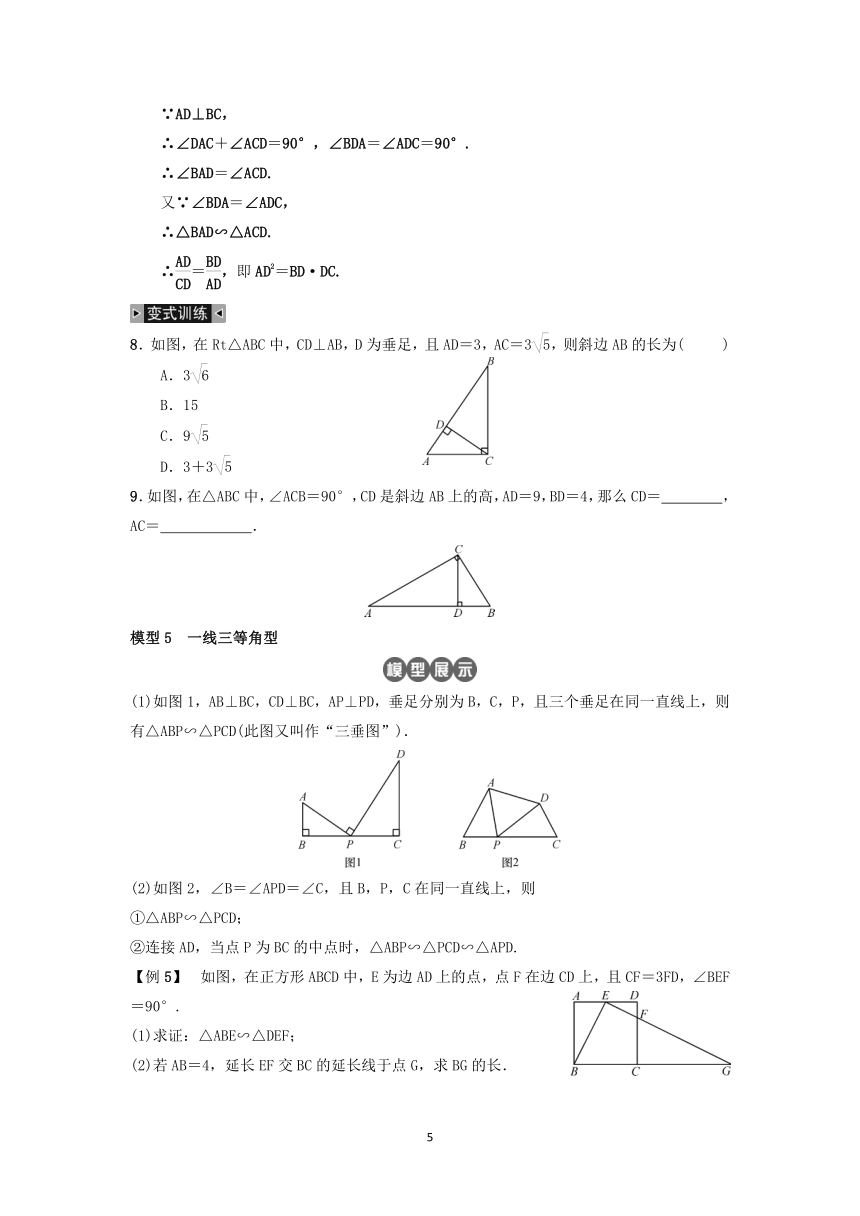
25761952139958.如图,在Rt△ABC中,CD⊥AB,D为垂足,且AD=3,AC=3,则斜边AB的长为( )
A.3
B.15
C.9
D.3+3
9.如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,AD=9,BD=4,那么CD= ,AC= .
模型5 一线三等角型
(1)如图1,AB⊥BC,CD⊥BC,AP⊥PD,垂足分别为B,C,P,且三个垂足在同一直线上,则有△ABP∽△PCD(此图又叫作“三垂图”).
(2)如图2,∠B=∠APD=∠C,且B,P,C在同一直线上,则
①△ABP∽△PCD;
②连接AD,当点P为BC的中点时,△ABP∽△PCD∽△APD.
3876040213360【例5】 如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°.
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长.
解:(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°.
∴∠ABE+∠AEB=90°.
又∵∠BEF=90°,
∴∠AEB+∠DEF=90°.
∴∠ABE=∠DEF.
∴△ABE∽△DEF.
(2)∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3.
∵△ABE∽△DEF,
∴=,即=.
∴DE=2.
又∵ED∥CG,∴△EDF∽△GCF.
∴=.∴GC=6.
∴BG=BC+CG=10.
10.如图,在等腰△ABC中,点E,F,O分别是腰AB,AC及底BC边上任意一点,且∠EOF=∠B=∠C.求证:OE·FC=FO·OB.
1.如图,在矩形ABCD中,作DF⊥AC,垂足为F,延长DF交AB于点E,在图中一定和△DFC相似的三角形有 个.
2.如图,已知△ABC,△DCE,△FEG,△HGI是4个全等的等腰三角形,底边BC,CE,EG,GI在同一条直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .
3.【分类讨论思想】如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为 .
4.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
专题2 相似三角形的性质与判定
类型1 利用相似三角形求线段长
1.如图,在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为 .
2.如图,已知菱形BEDF内接于△ABC,点E,D,F分别在AB,AC和BC上.若AB=15 cm,BC=12 cm,则菱形的边长为 cm.
3.如图,在△ABC中,AB=AC,点D,E分别在边BC,AB上,且∠ADE=∠B.如果DE∶AD=2∶5,BD=3,那么AC= .
4.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,在Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP= .
5.如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA的延长线于点E,点F是DE延长线上一点,连接AF.
(1)如果=,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
类型2 利用相似三角形求角度
6.如图,A,B,C,P四点均在边长为1的小正方形网格格点上,则∠BAC的度数是 .
7.如图,在等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且AB2=BD·CE.若∠BAC=40°,则∠DAE= .
类型3 利用相似三角形求比值
35820355575308.如图,AB∥DC,AC与BD交于点E,EF∥DC交BC于点F,CE=5,CF=4,AE=BC,则等于( )
A. B.
C. D.
29571951993909.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O.若S△DOE∶S△COA=1∶25,则S△BDE与S△CDE的比是( )
A.1∶3 B.1∶4
C.1∶5 D.1∶25
10.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E.若AB=3,BC=4,则的值为 .
类型4 利用相似三角形证明等积式与比例式
11.如图,在△ABC中,D,E分别是AB,AC上的点,且BD=2AD,CE=2AE.求证:
(1)△ADE∽△ABC;
(2)DF·BF=EF·CF.
12.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,E为AC的中点,ED,CB的延长线交于点F.求证:=.
类型5 利用相似求点的坐标
342201526543013.如图,在平面直角坐标系xOy中,A(-4,0),B(0,2),连接AB并延长到点C,连接CO.若△COB∽△CAO,则点C的坐标为( )
A.(1,) B.(,)
C.(,2) D.(,2)
14.如图,已知直线y=-x+2与x轴交于点A,与y轴交于点B,在x轴上有一点C,使B,O,C三点构成的三角形与△AOB相似,则点C的坐标为
专题3 圆与相似
36810952146301.如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC边于点E,AD=5,BD=2,则DE的长为( )
A. B.
C. D.
28733753695702.如图,已知⊙O是等腰Rt△ABC的外接圆,D是上一点,BD交AC于点E.若BC=4,AD=,则AE的长是( )
A.3 B.2
C.1 D.1.2
3.如图,⊙O的两弦AB,CD交于点P,连接AC,BD,得S△ACP∶S△DBP=16∶9,则AC∶BD= .
4.如图,已知AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交⊙O于点D,作PD∥AB,交CA的延长线于点P,连接AD,BD.求证:
(1)PD是⊙O的切线;
(2)△PAD∽△DBC.
5.如图,以△ABC的边AC为直径的⊙O交AB边于点M,交BC边于点N,连接AN,过点C的切线交AB的延长线于点P,∠BCP=∠BAN.求证:
(1)△ABC为等腰三角形;
(2)AM·CP=AN·CB.
6.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
参考答案:
专题1 相似三角形的基本模型
4.
2.证明:∵AF⊥DE,AG⊥BC,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC,
∴∠AEF=∠ACG.
又∵∠DAE=∠BAC,
∴△ADE∽△ABC.
3.D
4. .
5.解:∵∠ADE=∠ACB,
∴180°-∠ADE=180°-∠ACB,
即∠BDF=∠ECF.
又∵∠BFD=∠EFC,
∴△BDF∽△ECF.
∴=,即=.
∴DF=4.
6.B
7..
8.B
9.3.
10.证明:∵∠EOC=∠EOF+∠FOC,∠EOC=∠B+∠BEO,∠EOF=∠B,
∴∠FOC=∠OEB.
又∵∠B=∠C,
∴△BOE∽△CFO.
∴=,
即OE·FC=FO·OB.
5 .
2..
3.或3.
4.解:(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,且∠DEF=∠B,
∴∠BDE=∠CEF.
∴△BDE∽△CEF.
(2)∵△BDE∽△CEF,∴=.
∵点E是BC的中点,∴BE=CE.
∴=.∴=.
∵∠DEF=∠B=∠C,∴△DEF∽△ECF.
∴∠DFE=∠CFE,即FE平分∠DFC.
专题2 相似三角形的性质与判定
1.8.
2..
3..
4.3.
5.解:(1)∵DE∥BC,
∴△ADE∽△ABC.
∴=.∴=.
∴BC=9.
(2)∵∠FAE=∠B,∠B=∠D,
∴∠FAE=∠D.
又∵∠F=∠F,
∴△FAE∽△FDA.
∴=.
∴DF==9.
6.135°.
7.110°.
8.B
9.B
10..
11.证明:(1)∵BD=2AD,CE=2AE,
∴AB=3AD,AC=3AE.
∴==.
∵∠A=∠A,
∴△ADE∽△ABC.
(2)∵==,
∴DE∥BC.
∴△DEF∽△CBF.
∴=.
∴DF·BF=EF·CF.
12.证明:∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD,∠ACB=∠BDC=90°.
∴∠A=∠BCD.
∴△ABC∽△CBD.
∴=,即=.
又∵E为AC的中点,
∴AE=CE=ED.
∴∠A=∠EDA.
∵∠EDA=∠BDF,
∴∠FCD=∠BDF.
又∵∠F为公共角,
∴△FDB∽△FCD.
∴=.
∴=.
13.B
14. (-4,0)或(4,0)或(-1,0)或(1,0).
专题3 圆与相似
1.D
2.C
3.4∶3.
4.
证明:(1)连接OD.
∵∠DCA=∠DCB,
∴=.∴OD⊥AB.
∵AB∥PD,∴OD⊥PD.
∵点D在⊙O上,OD为⊙O的半径,
∴PD是⊙O的切线.
(2)∵∠PAD+∠CAD=180°,∠DBC+∠CAD=180°,
∴∠PAD=∠DBC.
由(1)可得:∠PDA=∠BCD=45°,
∴△PAD∽△DBC.
5.证明:(1)∵AC为⊙O的直径,
∴∠ANC=90°.
∵PC是⊙O的切线,
∴∠BCP=∠CAN.
∵∠BCP=∠BAN,∴∠BAN=∠CAN.
又∵AN⊥BC,
∴AB=AC.∴△ABC为等腰三角形.
(2)连接MN∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN.
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA.
∴=,即AM·CP=AN·CB.
6.
解:(1)证明:连接OE,
∵OB=OE,
∴∠OBE=∠OEB.
∵BE平分∠ABC,∠OBE=∠EBC.∴∠OEB=∠EBC.∴OE∥BC.
又∵∠C=90°,∴∠OEA=90°,即AC⊥OE.
又∵OE是⊙O的半径,∴AC是⊙O的切线.
(2)在△BCE与△BED中,
∵∠C=∠BED=90°,∠EBC=∠DBE,
∴△BCE∽△BED.
∴=,即BC=.
∵BE=4,BD是⊙O的直径,即BD=5,∴BC=.
又∵OE∥BC,∴=.∵AO=AD+2.5,AB=AD+5,∴=.
解得AD=.
模型1 A字型及其变形
(1)如图1,公共角所对的边平行(DE∥BC),则△ADE∽△ABC;
(2)如图2,公共角的对边不平行,且有另一组角相等(∠AED=∠ABC或∠ADE=∠ACB),则△AED∽△ABC.
【例1】 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,且∠ADE=∠B,DE=2,求AD·BC的值.
42989500解:∵∠ADE=∠B,∠EAD=∠CAB,
∴△ADE∽△ABC.
∴=.
∴AD·BC=DE·AB.
又∵DE=2,AB=5,
∴AD·BC=2×5=10.
1.如图,在△ABC中,DE∥BC,DF∥AC,AE=3,AC=5,BC=10,则BF的长为 .
2.如图,在锐角△ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.求证:△ADE∽△ABC.
模型2 X字型及其变形
(1)如图1,对顶角的对边平行(AB∥CD),则△ABO∽△DCO;
(2)如图2,对顶角的对边不平行,且有另一对角相等(∠B=∠D或∠A=∠C),则△ABO∽△CDO.
【例2】 如图,在四边形ABCD中,AB∥CD,对角线AC与BD相交于点O.求证:△ABO∽△CDO.
41313100证明:∵AB∥CD,
∴∠OAB=∠OCD,
∠OBA=∠ODC.
∴△ABO∽△CDO.
【补充设问】△AOD与△BOC相似吗?试说明理由.
解:△AOD与△BOC不相似.
理由如下:∵∠AOD=∠COB,
要使△AOD与△BOC相似,
∴当满足=或=时,
即DO·BO=AO·CO或DO·CO=AO·BO时,△AOD与△BOC相似.
由已证可知△ABO∽△CDO,∴=,
即AO·DO=BO·CO,不满足证明△AOD与△BOC相似的条件.
∴△AOD与△BOC不相似.
【变式】 如图,在四边形ABDC中,若AB不平行于CD,∠ABC=∠ADC,则图中的相似三角形有△COD∽△AOB,△AOC∽△BOD.
3.如图,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F,已知FG=2,则线段AE的长度为( )
A.6 B.8 C.10 D.12
4.将一副三角尺如图所示叠放在一起,则的值是 .
5.如图,已知∠ADE=∠ACB,BD=8,CE=4,CF=2,求DF的长.
模型3 子母型
若两个三角形有一个公共角和一条公共边,且有另一对角相等,则这两个三角形相似.如图,若∠ACD=∠B,则△ACD∽△ABC,从而可得结论:AC2=AD·AB.
【例3】 如图,P是△ABC的边AB上的一点.
(1)如果∠ACP=∠B,△ACP与△ABC是否相似?为什么?
(2)如果=,△ACP与△ABC是否相似?为什么?如果=呢?
42227500解:(1)△ACP∽△ABC.理由如下:
∵∠ACP=∠ABC,
∠PAC=∠CAB,
∴△ACP∽△ABC.
(2)=时,△ACP∽△ABC.理由如下:
∵∠PAC=∠CAB,且=,
∴△ACP∽△ABC.
由=不能得到△ACP与△ABC相似.
∵AC与CP的夹角为∠ACP,BC与AC的夹角为∠ACB,
而∠ACP与∠ACB不相等,
∴由=不能得到△ACP与△ABC相似.
6.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A.4 B.4 C.6 D.4
7.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A,若BC=2,AB=3,则BD的长为 .
模型4 双垂直型
直角三角形被斜边上的高分成的两个直角三角形与原三角形相似.如图,Rt△ABC中,CD为斜边AB上的高,则有△ACD∽△ABC∽△CBD,从而可得结论:CD2=BD·AD,BC2=BD·AB,AC2=AD·AB.
【例4】 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)请指出图中所有的相似三角形;
(2)你能得出AD2=BD·DC吗?41313100
解:(1)△BAD∽△BCA∽△ACD.
(2)能得出AD2=BD·DC.
理由如下:
∵∠BAC=90°,
∴∠BAD+∠DAC=90°.
∵AD⊥BC,
∴∠DAC+∠ACD=90°,∠BDA=∠ADC=90°.
∴∠BAD=∠ACD.
又∵∠BDA=∠ADC,
∴△BAD∽△ACD.
∴=,即AD2=BD·DC.
25761952139958.如图,在Rt△ABC中,CD⊥AB,D为垂足,且AD=3,AC=3,则斜边AB的长为( )
A.3
B.15
C.9
D.3+3
9.如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,AD=9,BD=4,那么CD= ,AC= .
模型5 一线三等角型
(1)如图1,AB⊥BC,CD⊥BC,AP⊥PD,垂足分别为B,C,P,且三个垂足在同一直线上,则有△ABP∽△PCD(此图又叫作“三垂图”).
(2)如图2,∠B=∠APD=∠C,且B,P,C在同一直线上,则
①△ABP∽△PCD;
②连接AD,当点P为BC的中点时,△ABP∽△PCD∽△APD.
3876040213360【例5】 如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°.
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长.
解:(1)证明:∵四边形ABCD为正方形,
∴∠A=∠D=90°.
∴∠ABE+∠AEB=90°.
又∵∠BEF=90°,
∴∠AEB+∠DEF=90°.
∴∠ABE=∠DEF.
∴△ABE∽△DEF.
(2)∵AB=BC=CD=AD=4,CF=3FD,
∴DF=1,CF=3.
∵△ABE∽△DEF,
∴=,即=.
∴DE=2.
又∵ED∥CG,∴△EDF∽△GCF.
∴=.∴GC=6.
∴BG=BC+CG=10.
10.如图,在等腰△ABC中,点E,F,O分别是腰AB,AC及底BC边上任意一点,且∠EOF=∠B=∠C.求证:OE·FC=FO·OB.
1.如图,在矩形ABCD中,作DF⊥AC,垂足为F,延长DF交AB于点E,在图中一定和△DFC相似的三角形有 个.
2.如图,已知△ABC,△DCE,△FEG,△HGI是4个全等的等腰三角形,底边BC,CE,EG,GI在同一条直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .
3.【分类讨论思想】如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为 .
4.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
专题2 相似三角形的性质与判定
类型1 利用相似三角形求线段长
1.如图,在△ABC中,AB=6,点D是AB的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且ME=DM.当AM⊥BM时,则BC的长为 .
2.如图,已知菱形BEDF内接于△ABC,点E,D,F分别在AB,AC和BC上.若AB=15 cm,BC=12 cm,则菱形的边长为 cm.
3.如图,在△ABC中,AB=AC,点D,E分别在边BC,AB上,且∠ADE=∠B.如果DE∶AD=2∶5,BD=3,那么AC= .
4.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,在Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP= .
5.如图,在△ABC中,点D是BA边延长线上一点,过点D作DE∥BC,交CA的延长线于点E,点F是DE延长线上一点,连接AF.
(1)如果=,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
类型2 利用相似三角形求角度
6.如图,A,B,C,P四点均在边长为1的小正方形网格格点上,则∠BAC的度数是 .
7.如图,在等腰△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且AB2=BD·CE.若∠BAC=40°,则∠DAE= .
类型3 利用相似三角形求比值
35820355575308.如图,AB∥DC,AC与BD交于点E,EF∥DC交BC于点F,CE=5,CF=4,AE=BC,则等于( )
A. B.
C. D.
29571951993909.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O.若S△DOE∶S△COA=1∶25,则S△BDE与S△CDE的比是( )
A.1∶3 B.1∶4
C.1∶5 D.1∶25
10.如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E.若AB=3,BC=4,则的值为 .
类型4 利用相似三角形证明等积式与比例式
11.如图,在△ABC中,D,E分别是AB,AC上的点,且BD=2AD,CE=2AE.求证:
(1)△ADE∽△ABC;
(2)DF·BF=EF·CF.
12.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,E为AC的中点,ED,CB的延长线交于点F.求证:=.
类型5 利用相似求点的坐标
342201526543013.如图,在平面直角坐标系xOy中,A(-4,0),B(0,2),连接AB并延长到点C,连接CO.若△COB∽△CAO,则点C的坐标为( )
A.(1,) B.(,)
C.(,2) D.(,2)
14.如图,已知直线y=-x+2与x轴交于点A,与y轴交于点B,在x轴上有一点C,使B,O,C三点构成的三角形与△AOB相似,则点C的坐标为
专题3 圆与相似
36810952146301.如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC边于点E,AD=5,BD=2,则DE的长为( )
A. B.
C. D.
28733753695702.如图,已知⊙O是等腰Rt△ABC的外接圆,D是上一点,BD交AC于点E.若BC=4,AD=,则AE的长是( )
A.3 B.2
C.1 D.1.2
3.如图,⊙O的两弦AB,CD交于点P,连接AC,BD,得S△ACP∶S△DBP=16∶9,则AC∶BD= .
4.如图,已知AB是⊙O的直径,C是⊙O上一点,∠ACB的平分线交⊙O于点D,作PD∥AB,交CA的延长线于点P,连接AD,BD.求证:
(1)PD是⊙O的切线;
(2)△PAD∽△DBC.
5.如图,以△ABC的边AC为直径的⊙O交AB边于点M,交BC边于点N,连接AN,过点C的切线交AB的延长线于点P,∠BCP=∠BAN.求证:
(1)△ABC为等腰三角形;
(2)AM·CP=AN·CB.
6.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
参考答案:
专题1 相似三角形的基本模型
4.
2.证明:∵AF⊥DE,AG⊥BC,
∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC,
∴∠AEF=∠ACG.
又∵∠DAE=∠BAC,
∴△ADE∽△ABC.
3.D
4. .
5.解:∵∠ADE=∠ACB,
∴180°-∠ADE=180°-∠ACB,
即∠BDF=∠ECF.
又∵∠BFD=∠EFC,
∴△BDF∽△ECF.
∴=,即=.
∴DF=4.
6.B
7..
8.B
9.3.
10.证明:∵∠EOC=∠EOF+∠FOC,∠EOC=∠B+∠BEO,∠EOF=∠B,
∴∠FOC=∠OEB.
又∵∠B=∠C,
∴△BOE∽△CFO.
∴=,
即OE·FC=FO·OB.
5 .
2..
3.或3.
4.解:(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,且∠DEF=∠B,
∴∠BDE=∠CEF.
∴△BDE∽△CEF.
(2)∵△BDE∽△CEF,∴=.
∵点E是BC的中点,∴BE=CE.
∴=.∴=.
∵∠DEF=∠B=∠C,∴△DEF∽△ECF.
∴∠DFE=∠CFE,即FE平分∠DFC.
专题2 相似三角形的性质与判定
1.8.
2..
3..
4.3.
5.解:(1)∵DE∥BC,
∴△ADE∽△ABC.
∴=.∴=.
∴BC=9.
(2)∵∠FAE=∠B,∠B=∠D,
∴∠FAE=∠D.
又∵∠F=∠F,
∴△FAE∽△FDA.
∴=.
∴DF==9.
6.135°.
7.110°.
8.B
9.B
10..
11.证明:(1)∵BD=2AD,CE=2AE,
∴AB=3AD,AC=3AE.
∴==.
∵∠A=∠A,
∴△ADE∽△ABC.
(2)∵==,
∴DE∥BC.
∴△DEF∽△CBF.
∴=.
∴DF·BF=EF·CF.
12.证明:∵∠ACB=90°,CD⊥AB,
∴∠A+∠ACD=∠ACD+∠BCD,∠ACB=∠BDC=90°.
∴∠A=∠BCD.
∴△ABC∽△CBD.
∴=,即=.
又∵E为AC的中点,
∴AE=CE=ED.
∴∠A=∠EDA.
∵∠EDA=∠BDF,
∴∠FCD=∠BDF.
又∵∠F为公共角,
∴△FDB∽△FCD.
∴=.
∴=.
13.B
14. (-4,0)或(4,0)或(-1,0)或(1,0).
专题3 圆与相似
1.D
2.C
3.4∶3.
4.
证明:(1)连接OD.
∵∠DCA=∠DCB,
∴=.∴OD⊥AB.
∵AB∥PD,∴OD⊥PD.
∵点D在⊙O上,OD为⊙O的半径,
∴PD是⊙O的切线.
(2)∵∠PAD+∠CAD=180°,∠DBC+∠CAD=180°,
∴∠PAD=∠DBC.
由(1)可得:∠PDA=∠BCD=45°,
∴△PAD∽△DBC.
5.证明:(1)∵AC为⊙O的直径,
∴∠ANC=90°.
∵PC是⊙O的切线,
∴∠BCP=∠CAN.
∵∠BCP=∠BAN,∴∠BAN=∠CAN.
又∵AN⊥BC,
∴AB=AC.∴△ABC为等腰三角形.
(2)连接MN∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN.
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA.
∴=,即AM·CP=AN·CB.
6.
解:(1)证明:连接OE,
∵OB=OE,
∴∠OBE=∠OEB.
∵BE平分∠ABC,∠OBE=∠EBC.∴∠OEB=∠EBC.∴OE∥BC.
又∵∠C=90°,∴∠OEA=90°,即AC⊥OE.
又∵OE是⊙O的半径,∴AC是⊙O的切线.
(2)在△BCE与△BED中,
∵∠C=∠BED=90°,∠EBC=∠DBE,
∴△BCE∽△BED.
∴=,即BC=.
∵BE=4,BD是⊙O的直径,即BD=5,∴BC=.
又∵OE∥BC,∴=.∵AO=AD+2.5,AB=AD+5,∴=.
解得AD=.
