人教版数学九年级下册数学27.2.1 相似三角形的判定同步练习(word版附答案)
文档属性
| 名称 | 人教版数学九年级下册数学27.2.1 相似三角形的判定同步练习(word版附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 220.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 12:50:08 | ||
图片预览


文档简介
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
30257752660651.如图所示,△ADE∽△ACB,∠AED=∠B,那么下列比例式成立的是( )
A.== B.=
C.== D.==
2.两个三角形相似,且相似比k=1,则这两个三角形 .
3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
4.如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C,直线DF交l1,l2,l3于点D,E,F,已知=,则= .
5.如图,在?ABCD中,EF∥AB交AD于点E,交BD于点F,DE∶EA=3∶4,EF=3,则CD的长为( )
A.4 B.7 C.3 D.12
6.如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
A.4对 B.3对 C.2对 D.1对
7.在△ABC中,AB=6,AC=9,点P是直线AB上一点,且AP=2,过点P作BC边的平行线,交直线AC于点M,则MC的长为 .
8.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
1936115179070A.=
B.=
C.=
D.=
22186902463809.如图,AG∶GD=4∶1,BD∶DC=2∶3,则AE∶EC的值是( )
A.3∶2
B.4∶3
C.6∶5
D.8∶5
10.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上,若线段AB=4 cm,则线段BC= cm.
11.如图,在△ABC中,点D,E分别为AB,AC的中点,连接DE,线段BE,CD相交于点O,若OD=2,则OC= .
12.如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若CD=5,BC=8,AE=2,则AF= .
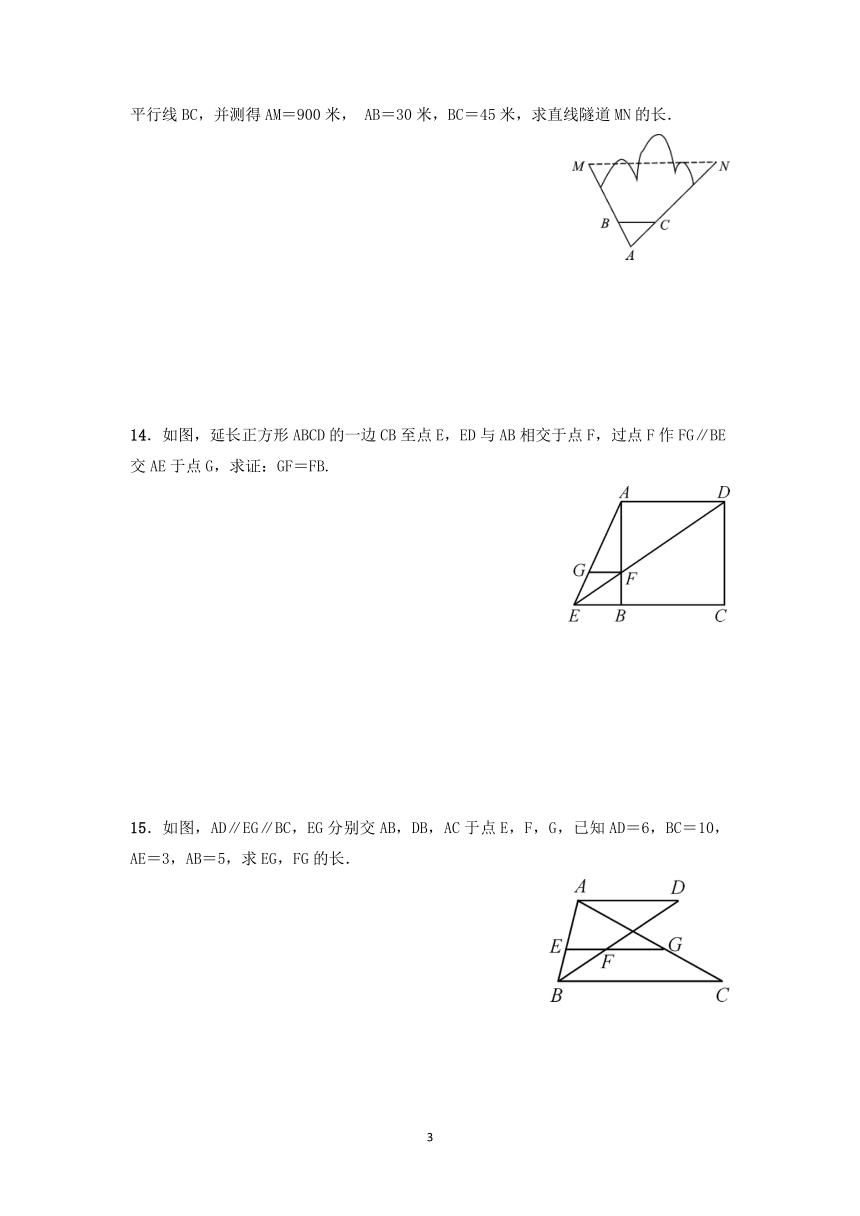
13.中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”,修建高铁时常常要逢山开道、遇水搭桥,如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算M、N两点之间的直线距离,选择作MN的平行线BC,并测得AM=900米, AB=30米,BC=45米,求直线隧道MN的长.
14.如图,延长正方形ABCD的一边CB至点E,ED与AB相交于点F,过点F作FG∥BE交AE于点G,求证:GF=FB.
15.如图,AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=6,BC=10,AE=3,AB=5,求EG,FG的长.
第2课时 相似三角形的判定定理1,2
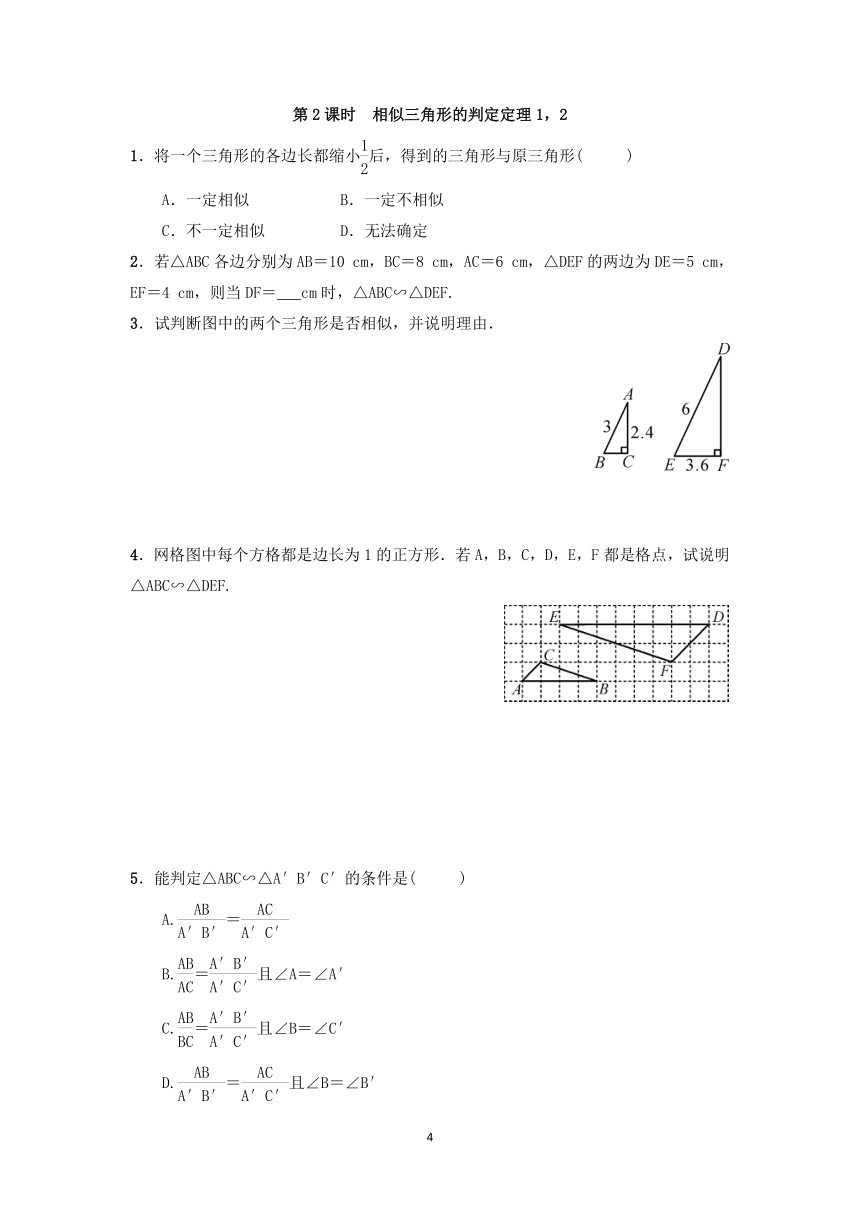
1.将一个三角形的各边长都缩小后,得到的三角形与原三角形( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法确定
2.若△ABC各边分别为AB=10 cm,BC=8 cm,AC=6 cm,△DEF的两边为DE=5 cm,EF=4 cm,则当DF= cm时,△ABC∽△DEF.
3.试判断图中的两个三角形是否相似,并说明理由.
4.网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
5.能判定△ABC∽△A′B′C′的条件是( )
A.=
B.=且∠A=∠A′
C.=且∠B=∠C′
D.=且∠B=∠B′
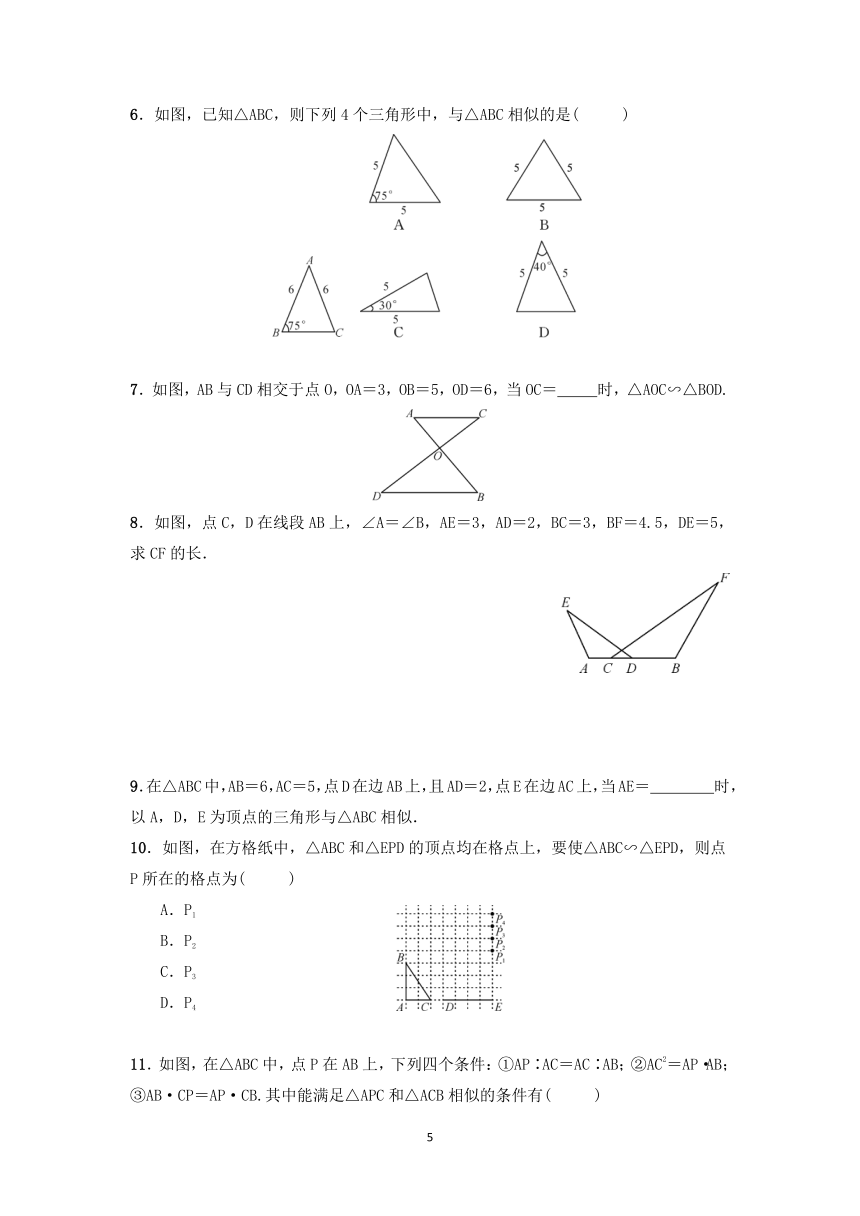
6.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
7.如图,AB与CD相交于点O,OA=3,OB=5,OD=6,当OC= 时,△AOC∽△BOD.
8.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
9.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE= 时,以A,D,E为顶点的三角形与△ABC相似.
10.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
234124553340A.P1
B.P2
C.P3
D.P4
11.如图,在△ABC中,点P在AB上,下列四个条件:①AP∶AC=AC∶AB;②AC2=AP·AB;③AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件有( )
A.1个 B.2个 C.3个 D.0个
12.如图,已知∠DAB=∠CAE,请补充一个条件: ,使△ABC∽△ADE.
13.如图,AB∥DE,AC∥DF,BC∥EF,求证:△DEF∽△ABC.
14.如图,在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:△ADB∽△EAC.
15.如图,正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
16.如图,在钝角三角形ABC中,AB=6 cm,AC=12 cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1 cm/s,点E运动的速度为2 cm/s.如果两点同时运动,那么当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间是 .
第3课时 相似三角形的判定定理3
1.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
2.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是 .
3.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形 .(用相似符号连接)
4.如图,点B,D,C,F在一条直线上,且AB∥EF,AC∥DE,求证:△ABC∽△EFD.
5.如图,∠1=∠2,∠C=∠D.求证:△ABC∽△AED.
6.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′= 时,△ABC∽△A′B′C′.
7.一个直角三角形的一条直角边长和斜边长分别为8 cm和15 cm,另一个直角三角形的一条直角边长和斜边长分别是6 cm和 cm,这两个直角三角形 (填“是”或“不是”)相似三角形.
8.一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长分别为2和4,那么这两个直角三角形 (填“一定”“不一定”或“一定不”)相似.
9.如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,且∠DCE=∠B.那么下列判断中,错误的是( )
238569555880A.△ADE∽△ABC
B.△ADE∽△ACD
C.△DEC∽△CDB
D.△ADE∽△DCB
10.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( )
24923755080A.2
B.4
C.6
D.8
11.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
12.如图,已知∠ACB=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似?
13.如图,在?ABCD中,过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.求证:△ABF∽△BEC.
14.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
15.如图,在△ABC中,AD,BF分别是BC,AC边上的高,过点D作AB的垂线交AB于点E,交BF于点G,交AC的延长线于点H,求证:DE2=EG·EH.
参考答案:
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1.A
2. 全等.
3.B
4. 2.
5.B
6.B
7. 6或12.
8.D
9.D
10.12.
11.4.
12..
13.解:∵BC∥MN,
∴△ABC∽△AMN.
∴=,即=.
∴MN=1 350.
答: 直线隧道MN的长为1 350米.
14.证明:∵GF∥AD,
∴=.
又FB∥DC,∴=.
又AD=DC,∴=.
∴GF=FB.
15.解:∵在△ABC中,EG∥BC,
∴△AEG∽△ABC,
∴=.
∵BC=10,AE=3,AB=5,
∴=,∴EG=6.
∵在△BAD中,EF∥AD,
∴△BEF∽△BAD,∴=.
∵AD=6,AE=3,AB=5,
∴=.∴EF=.
∴FG=EG-EF=.
第2课时 相似三角形的判定定理1,2
1.A
2.3.
3.解:相似.理由如下:
在Rt△ABC中,BC===1.8,
在Rt△DEF中,
DF===4.8,
∴===.
∴△ABC∽△DEF.
4.证明:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8,
∴===.
∴△ABC∽△DEF.
5.B
6.C
7.
8.解:∵==,=,∴=.
又∵∠A=∠B,∴△AED∽△BFC.
∴=.∴=.
∴CF=.
或 .
10.C
11.B
12. =
13.证明:∵AB∥DE,
∴△ODE∽△OAB.
∴=.
∵BC∥EF,
∴△OEF∽△OBC.
∴==.
∵AC∥DF,
∴△ODF∽△OAC.
∴=.
∴==.
∴△DEF∽△ABC.
14.证明:∵AB=AC,
∴∠ABC=∠ACB.
∴∠ABD=∠ACE.
∵AB2=DB·CE,∴=.
又AB=AC,∴=.
∴△ADB∽△EAC.
15.证明:设正方形的边长为4a,则AD=CD=BC=4a.
∵Q是CD的中点,BP=3PC,
∴DQ=CQ=2a,PC=a.
∴==.
又∵∠D=∠C=90°,
∴△ADQ∽△QCP.
16.3__s或4.8__s.
第3课时 相似三角形的判定定理3
1.A
2. △EFD,△HGK.
3. 答案不唯一,如△BDE∽△CDF,△ABF∽△ACE等.
4.证明:∵AB∥EF,AC∥DE,
∴∠B=∠F,∠ACB=∠EDF.
∴△ABC∽△EFD.
5.证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAC=∠EAD.
又∵∠C=∠D,
∴△ABC∽△AED.
6.10.
7.是.
8.不一定.
9.D
10.B
11..
12.解:①若△ABC∽△ADB,
则=.∴AD=3;
②若△ABC∽△DAB,
则=.∴AD=3.
综上所述,当AD=3或3时,两直角三角形相似.
13.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC.
∴∠D+∠C=180°,∠ABF=∠BEC.
又∵∠AFB+∠AFE=180°,且∠AFE=∠D,
∴∠C=∠AFB.
又∵∠ABF=∠BEC,
∴△ABF∽△BEC.
14.解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴△APQ∽△CDQ.
(2)当DP⊥AC时,∠QCD+∠QDC=90°.
∵∠ADQ+∠QDC=90°,∴∠DCA=∠ADP.
又∵∠ADC=∠DAP=90°,
∴△ADC∽△PAD.
∴=.∴=,解得PA=5.
∴t=5.
15.证明:∵AD,BF分别是BC,AC边上的高,
∴∠ADB=∠BED=90°.
∴∠EBD+∠EDB=∠EDB+∠ADE.
∴∠EBD=∠EDA.
∴△AED∽△DEB.
∴=,即DE2=AE·BE.
又∵∠HFG=90°,∠BGE=∠HGF,
∴∠EBG=∠H.
∵∠BEG=∠HEA=90°,
∴△BEG∽△HEA.
∴=,即EG·EH=AE·BE.
∴DE2=EG·EH.
第1课时 平行线分线段成比例
30257752660651.如图所示,△ADE∽△ACB,∠AED=∠B,那么下列比例式成立的是( )
A.== B.=
C.== D.==
2.两个三角形相似,且相似比k=1,则这两个三角形 .
3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
4.如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C,直线DF交l1,l2,l3于点D,E,F,已知=,则= .
5.如图,在?ABCD中,EF∥AB交AD于点E,交BD于点F,DE∶EA=3∶4,EF=3,则CD的长为( )
A.4 B.7 C.3 D.12
6.如图,点E,F分别在△ABC的边AB,AC上,且EF∥BC,点M在边BC上,AM与EF交于点D,则图中相似三角形共有( )
A.4对 B.3对 C.2对 D.1对
7.在△ABC中,AB=6,AC=9,点P是直线AB上一点,且AP=2,过点P作BC边的平行线,交直线AC于点M,则MC的长为 .
8.如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
1936115179070A.=
B.=
C.=
D.=
22186902463809.如图,AG∶GD=4∶1,BD∶DC=2∶3,则AE∶EC的值是( )
A.3∶2
B.4∶3
C.6∶5
D.8∶5
10.如图,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上,若线段AB=4 cm,则线段BC= cm.
11.如图,在△ABC中,点D,E分别为AB,AC的中点,连接DE,线段BE,CD相交于点O,若OD=2,则OC= .
12.如图,在?ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若CD=5,BC=8,AE=2,则AF= .
13.中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”,修建高铁时常常要逢山开道、遇水搭桥,如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算M、N两点之间的直线距离,选择作MN的平行线BC,并测得AM=900米, AB=30米,BC=45米,求直线隧道MN的长.
14.如图,延长正方形ABCD的一边CB至点E,ED与AB相交于点F,过点F作FG∥BE交AE于点G,求证:GF=FB.
15.如图,AD∥EG∥BC,EG分别交AB,DB,AC于点E,F,G,已知AD=6,BC=10,AE=3,AB=5,求EG,FG的长.
第2课时 相似三角形的判定定理1,2
1.将一个三角形的各边长都缩小后,得到的三角形与原三角形( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法确定
2.若△ABC各边分别为AB=10 cm,BC=8 cm,AC=6 cm,△DEF的两边为DE=5 cm,EF=4 cm,则当DF= cm时,△ABC∽△DEF.
3.试判断图中的两个三角形是否相似,并说明理由.
4.网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
5.能判定△ABC∽△A′B′C′的条件是( )
A.=
B.=且∠A=∠A′
C.=且∠B=∠C′
D.=且∠B=∠B′
6.如图,已知△ABC,则下列4个三角形中,与△ABC相似的是( )
7.如图,AB与CD相交于点O,OA=3,OB=5,OD=6,当OC= 时,△AOC∽△BOD.
8.如图,点C,D在线段AB上,∠A=∠B,AE=3,AD=2,BC=3,BF=4.5,DE=5,求CF的长.
9.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE= 时,以A,D,E为顶点的三角形与△ABC相似.
10.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
234124553340A.P1
B.P2
C.P3
D.P4
11.如图,在△ABC中,点P在AB上,下列四个条件:①AP∶AC=AC∶AB;②AC2=AP·AB;③AB·CP=AP·CB.其中能满足△APC和△ACB相似的条件有( )
A.1个 B.2个 C.3个 D.0个
12.如图,已知∠DAB=∠CAE,请补充一个条件: ,使△ABC∽△ADE.
13.如图,AB∥DE,AC∥DF,BC∥EF,求证:△DEF∽△ABC.
14.如图,在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB·CE.求证:△ADB∽△EAC.
15.如图,正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
16.如图,在钝角三角形ABC中,AB=6 cm,AC=12 cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1 cm/s,点E运动的速度为2 cm/s.如果两点同时运动,那么当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间是 .
第3课时 相似三角形的判定定理3
1.下列各组图形中有可能不相似的是( )
A.各有一个角是45°的两个等腰三角形
B.各有一个角是60°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
2.已知△ABC中,∠A=40°,∠B=75°,下图各三角形中与△ABC相似的是 .
3.如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形 .(用相似符号连接)
4.如图,点B,D,C,F在一条直线上,且AB∥EF,AC∥DE,求证:△ABC∽△EFD.
5.如图,∠1=∠2,∠C=∠D.求证:△ABC∽△AED.
6.在△ABC和△A′B′C′中,∠C=∠C′=90°,AC=12,AB=15,A′C′=8,则当A′B′= 时,△ABC∽△A′B′C′.
7.一个直角三角形的一条直角边长和斜边长分别为8 cm和15 cm,另一个直角三角形的一条直角边长和斜边长分别是6 cm和 cm,这两个直角三角形 (填“是”或“不是”)相似三角形.
8.一个直角三角形的两边长分别为3和6,另一个直角三角形的两边长分别为2和4,那么这两个直角三角形 (填“一定”“不一定”或“一定不”)相似.
9.如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,且∠DCE=∠B.那么下列判断中,错误的是( )
238569555880A.△ADE∽△ABC
B.△ADE∽△ACD
C.△DEC∽△CDB
D.△ADE∽△DCB
10.如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( )
24923755080A.2
B.4
C.6
D.8
11.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
12.如图,已知∠ACB=∠ABD=90°,AB=,AC=2,求AD的长为多少时,图中两直角三角形相似?
13.如图,在?ABCD中,过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.求证:△ABF∽△BEC.
14.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?
15.如图,在△ABC中,AD,BF分别是BC,AC边上的高,过点D作AB的垂线交AB于点E,交BF于点G,交AC的延长线于点H,求证:DE2=EG·EH.
参考答案:
27.2.1 相似三角形的判定
第1课时 平行线分线段成比例
1.A
2. 全等.
3.B
4. 2.
5.B
6.B
7. 6或12.
8.D
9.D
10.12.
11.4.
12..
13.解:∵BC∥MN,
∴△ABC∽△AMN.
∴=,即=.
∴MN=1 350.
答: 直线隧道MN的长为1 350米.
14.证明:∵GF∥AD,
∴=.
又FB∥DC,∴=.
又AD=DC,∴=.
∴GF=FB.
15.解:∵在△ABC中,EG∥BC,
∴△AEG∽△ABC,
∴=.
∵BC=10,AE=3,AB=5,
∴=,∴EG=6.
∵在△BAD中,EF∥AD,
∴△BEF∽△BAD,∴=.
∵AD=6,AE=3,AB=5,
∴=.∴EF=.
∴FG=EG-EF=.
第2课时 相似三角形的判定定理1,2
1.A
2.3.
3.解:相似.理由如下:
在Rt△ABC中,BC===1.8,
在Rt△DEF中,
DF===4.8,
∴===.
∴△ABC∽△DEF.
4.证明:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8,
∴===.
∴△ABC∽△DEF.
5.B
6.C
7.
8.解:∵==,=,∴=.
又∵∠A=∠B,∴△AED∽△BFC.
∴=.∴=.
∴CF=.
或 .
10.C
11.B
12. =
13.证明:∵AB∥DE,
∴△ODE∽△OAB.
∴=.
∵BC∥EF,
∴△OEF∽△OBC.
∴==.
∵AC∥DF,
∴△ODF∽△OAC.
∴=.
∴==.
∴△DEF∽△ABC.
14.证明:∵AB=AC,
∴∠ABC=∠ACB.
∴∠ABD=∠ACE.
∵AB2=DB·CE,∴=.
又AB=AC,∴=.
∴△ADB∽△EAC.
15.证明:设正方形的边长为4a,则AD=CD=BC=4a.
∵Q是CD的中点,BP=3PC,
∴DQ=CQ=2a,PC=a.
∴==.
又∵∠D=∠C=90°,
∴△ADQ∽△QCP.
16.3__s或4.8__s.
第3课时 相似三角形的判定定理3
1.A
2. △EFD,△HGK.
3. 答案不唯一,如△BDE∽△CDF,△ABF∽△ACE等.
4.证明:∵AB∥EF,AC∥DE,
∴∠B=∠F,∠ACB=∠EDF.
∴△ABC∽△EFD.
5.证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAC=∠EAD.
又∵∠C=∠D,
∴△ABC∽△AED.
6.10.
7.是.
8.不一定.
9.D
10.B
11..
12.解:①若△ABC∽△ADB,
则=.∴AD=3;
②若△ABC∽△DAB,
则=.∴AD=3.
综上所述,当AD=3或3时,两直角三角形相似.
13.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AD=BC.
∴∠D+∠C=180°,∠ABF=∠BEC.
又∵∠AFB+∠AFE=180°,且∠AFE=∠D,
∴∠C=∠AFB.
又∵∠ABF=∠BEC,
∴△ABF∽△BEC.
14.解:(1)证明:∵四边形ABCD是矩形,
∴AB∥CD.
∴△APQ∽△CDQ.
(2)当DP⊥AC时,∠QCD+∠QDC=90°.
∵∠ADQ+∠QDC=90°,∴∠DCA=∠ADP.
又∵∠ADC=∠DAP=90°,
∴△ADC∽△PAD.
∴=.∴=,解得PA=5.
∴t=5.
15.证明:∵AD,BF分别是BC,AC边上的高,
∴∠ADB=∠BED=90°.
∴∠EBD+∠EDB=∠EDB+∠ADE.
∴∠EBD=∠EDA.
∴△AED∽△DEB.
∴=,即DE2=AE·BE.
又∵∠HFG=90°,∠BGE=∠HGF,
∴∠EBG=∠H.
∵∠BEG=∠HEA=90°,
∴△BEG∽△HEA.
∴=,即EG·EH=AE·BE.
∴DE2=EG·EH.
