人教版数学九年级下册数学27.3 位似同步练习(word版附答案)
文档属性
| 名称 | 人教版数学九年级下册数学27.3 位似同步练习(word版附答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 294.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览




文档简介
27.3 位似
第1课时 位似图形的概念及画法
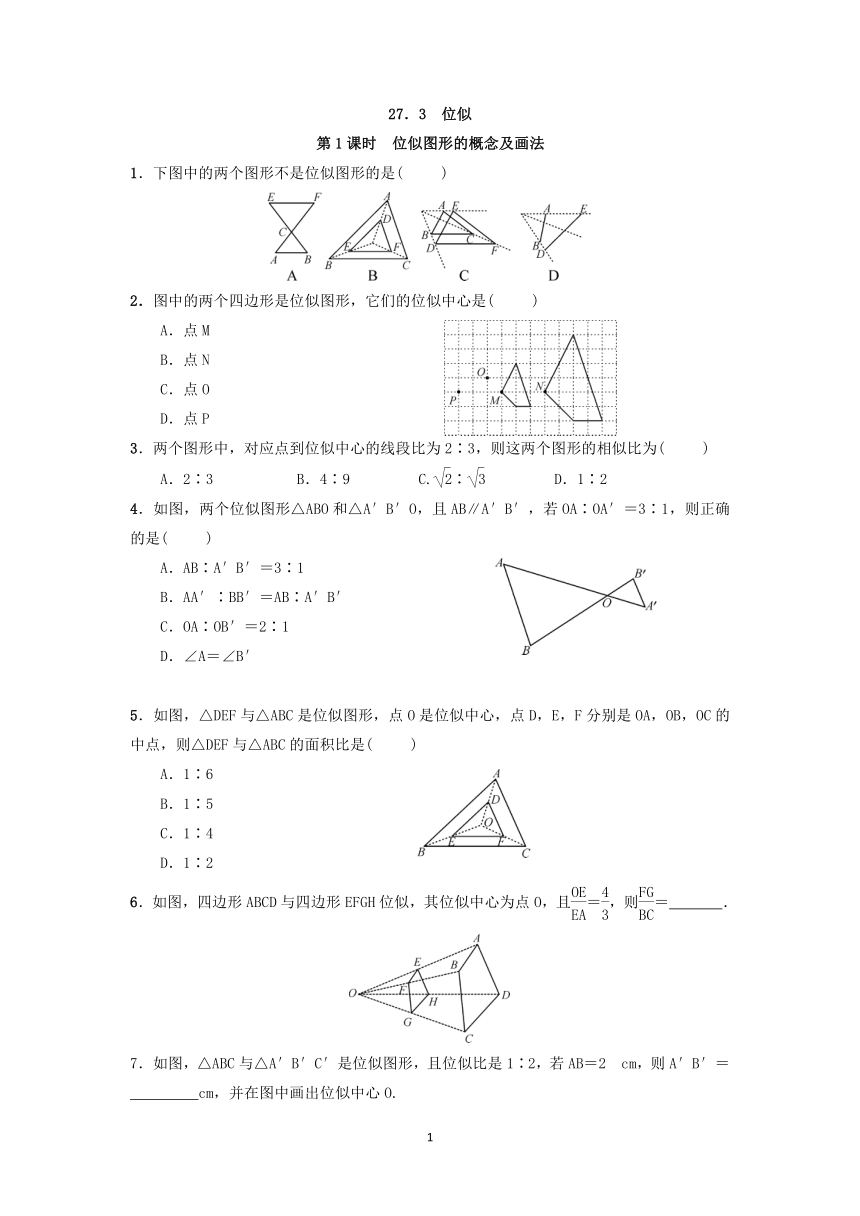
1.下图中的两个图形不是位似图形的是( )
2.图中的两个四边形是位似图形,它们的位似中心是( )
27666951270A.点M
B.点N
C.点O
D.点P
3.两个图形中,对应点到位似中心的线段比为2∶3,则这两个图形的相似比为( )
A.2∶3 B.4∶9 C.∶ D.1∶2
4.如图,两个位似图形△ABO和△A′B′O,且AB∥A′B′,若OA∶OA′=3∶1,则正确的是( )
32124658890A.AB∶A′B′=3∶1
B.AA′∶BB′=AB∶A′B′
C.OA∶OB′=2∶1
D.∠A=∠B′
5.如图,△DEF与△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
252349047625A.1∶6
B.1∶5
C.1∶4
D.1∶2
6.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则= .
如图,△ABC与△A′B′C′是位似图形,且位似比是1∶2,若AB=2 cm,则A′B′=
cm,并在图中画出位似中心O.
8.如图,以O点为位似中心,将四边形ABCD缩小为原来的一半.
9.如图,边长为1的正方形网格纸中,△ABC为格点三角形(顶点都在格点上).在网格纸中,以点O为位似中心画出△ABC的一个位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为1∶2.(只需画出一个符合条件的△A′B′C′,不要求写画法)
10.如图,三个正六边形全等,其中成位似图形关系的有( )
285051562230A.0对
B.1对
C.2对
D.3对
11.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
12.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2∶3
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
13.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心O;
(2)求出△ABC与△A′B′C′的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
14.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若=3,S四边形BCDE=20,求S四边形B′C′D′E′.
第2课时 平面直角坐标系中的位似
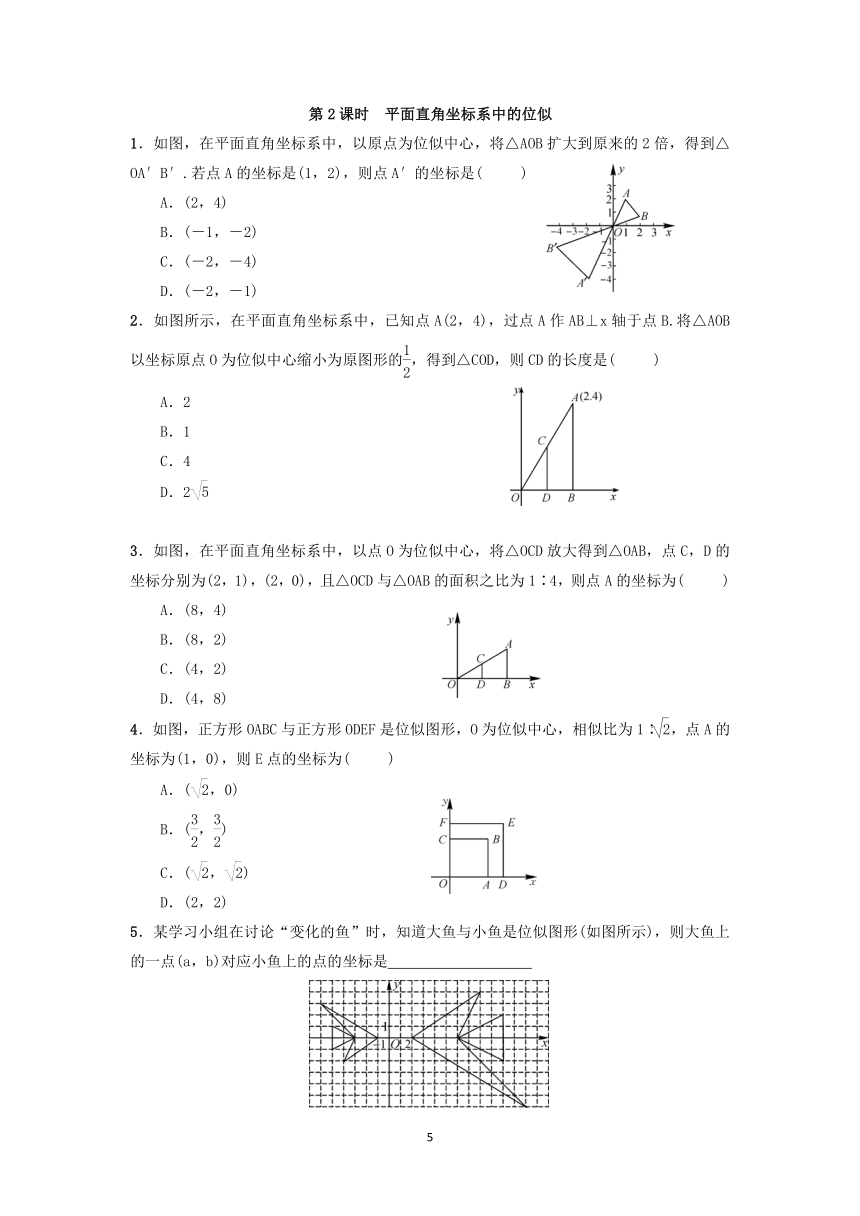
36582352755901.如图,在平面直角坐标系中,以原点为位似中心,将△AOB扩大到原来的2倍,得到△OA′B′.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
33458156762752.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是( )
A.2
B.1
C.4
D.2
3.如图,在平面直角坐标系中,以点O为位似中心,将△OCD放大得到△OAB,点C,D的坐标分别为(2,1),(2,0),且△OCD与△OAB的面积之比为1∶4,则点A的坐标为( )
2743835107950A.(8,4)
B.(8,2)
C.(4,2)
D.(4,8)
4.如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1∶,点A的坐标为(1,0),则E点的坐标为( )
2652395178435A.(,0)
B.(,)
C.(,)
D.(2,2)
5.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则大鱼上的一点(a,b)对应小鱼上的点的坐标是
6.如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.
7.如图,在平面直角坐标系中,作出五边形ABCDE的位似图形,使得新图形A1B1C1D1E1与原图形对应线段的比为2∶1,位似中心是坐标原点O.
8.在平面直角坐标系中,点C,D的坐标分别为C(2,3),D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为
9.在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心,把△AOB放大到原来的两倍,则点P的对应点的坐标为( )
A.(2m,2n) B.(2m,2n)或(-2m,-2n)
C.(m,n) D.(m,n)或(-m,-n)
257619561023510.如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2)
B.(-9,18)
C.(-9,18)或(9,-18)
D.(-1,2)或(1,-2)
11.如图,原点O是△ABC和△A′B′C′的位似中心,点A(1,0)与A′(-2,0)是对应点,△ABC的面积是,则△A′B′C′的面积是 .
12.如图,网格中每个小正方形的边长为1,已知△ABC,画出△ABC以坐标原点O为位似中心的位似图形△A′B′C′,使△A′B′C′在第三象限,与△ABC的位似比为,写出三角形各顶点的坐标,位似变换后对应顶点的坐标发生了什么变化?
13.如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
(1)写出正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心的坐标;
(2)正方形A4A5B4C4四个顶点的坐标.
14.如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即S△A1B1C1∶S△A2B2C2=1∶4.(不写解答过程,直接写出结果)
参考答案:
27.3 位似
第1课时 位似图形的概念及画法
1.D
2.D
3.A
4.A
5.C
6.=.
7.4.
解:如图所示.
8.解:图略.
9.
解:如图所示.
10.D
11.A
12.B
13.
解:(1)位似中心O的位置如图所示.
(2)∵=,
∴△ABC与△A′B′C′的相似比为1∶2.
(3)如图所示.
14.解:(1)证明:∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴======,
∠AB′C′=∠ABC,∠AC′B′=∠ACB,∠AC′D′=∠ACD,∠AD′C′=∠ADC,∠AD′E′=∠ADE,∠AE′D′=∠AED.
∴∠AC′B′+∠AC′D′=∠ACB+∠ACD,
∠AD′C′+∠AD′E′=∠ADC+∠ADE,
即∠B′C′D′=∠BCD,∠C′D′E′=∠CDE.
∵=,∠B′AE′=∠BAE,
∴△B′AE′∽△BAE.
∴=,∠AE′B′=∠AEB,∠AB′E′=∠ABE.
∴===,
∠AB′C′-∠AB′E′=∠ABC-∠ABE,
∠AE′D′-∠AE′B′=∠AED-∠AEB,
即∠E′B′C′=∠EBC,∠B′E′D′=∠BED.
∴四边形BCDE与四边形B′C′D′E′是相似图形.
又∵四边形BCDE与四边形B′C′D′E′对应顶点相交于一点A,
∴四边形BCDE位似于四边形B′C′D′E′.
(2)∵=3,∴=.
∴四边形BCDE与四边形B′C′D′E′位似之比为.
∵S四边形BCDE=20,
∴S四边形B′C′D′E′==20×=.
第2课时 平面直角坐标系中的位似
1.C
2.A
3.C
4.C
5. (-0.5a,-0.5b).
6.解:∵点B的坐标是(4,0),点D的坐标是(6,0),
∴OB=4,OD=6.
∴==.
∵△OAB与△OCD关于点O位似,
∴△OAB与△OCD的相似比为.
7.
解:如图所示.
(4,6)或(-4,-6).
9.B
10.D
11. 6.
12.
解:△ABC三个顶点的坐标分别是A(2,2),B(6,4),C(4,6).△A′B′C′三个顶点的坐标分别是A′(-1,-1),B′(-3,-2),C′(-2,-3).观察图形可知,△A′B′C′各顶点的坐标分别是将△ABC各对应顶点的坐标乘-.
13.解:(1)正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心的坐标为(0,0).
(2)∵点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0),
∴OA1=A1C1=1,OA2=A2C2=2.
∴A3O=A3C3=4.
∴OA4=A4C4=8.∴OA5=16.
∴A4(8,0),A5(16,0),B4(16,8),C4(8,8).
14.
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
第1课时 位似图形的概念及画法
1.下图中的两个图形不是位似图形的是( )
2.图中的两个四边形是位似图形,它们的位似中心是( )
27666951270A.点M
B.点N
C.点O
D.点P
3.两个图形中,对应点到位似中心的线段比为2∶3,则这两个图形的相似比为( )
A.2∶3 B.4∶9 C.∶ D.1∶2
4.如图,两个位似图形△ABO和△A′B′O,且AB∥A′B′,若OA∶OA′=3∶1,则正确的是( )
32124658890A.AB∶A′B′=3∶1
B.AA′∶BB′=AB∶A′B′
C.OA∶OB′=2∶1
D.∠A=∠B′
5.如图,△DEF与△ABC是位似图形,点O是位似中心,点D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
252349047625A.1∶6
B.1∶5
C.1∶4
D.1∶2
6.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则= .
如图,△ABC与△A′B′C′是位似图形,且位似比是1∶2,若AB=2 cm,则A′B′=
cm,并在图中画出位似中心O.
8.如图,以O点为位似中心,将四边形ABCD缩小为原来的一半.
9.如图,边长为1的正方形网格纸中,△ABC为格点三角形(顶点都在格点上).在网格纸中,以点O为位似中心画出△ABC的一个位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为1∶2.(只需画出一个符合条件的△A′B′C′,不要求写画法)
10.如图,三个正六边形全等,其中成位似图形关系的有( )
285051562230A.0对
B.1对
C.2对
D.3对
11.下列关于位似图形的表述:
①相似图形一定是位似图形,位似图形一定是相似图形;
②位似图形一定有位似中心;
③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
④位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③ B.①② C.③④ D.②③④
12.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是( )
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2∶3
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
13.如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心O;
(2)求出△ABC与△A′B′C′的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
14.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若=3,S四边形BCDE=20,求S四边形B′C′D′E′.
第2课时 平面直角坐标系中的位似
36582352755901.如图,在平面直角坐标系中,以原点为位似中心,将△AOB扩大到原来的2倍,得到△OA′B′.若点A的坐标是(1,2),则点A′的坐标是( )
A.(2,4)
B.(-1,-2)
C.(-2,-4)
D.(-2,-1)
33458156762752.如图所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原图形的,得到△COD,则CD的长度是( )
A.2
B.1
C.4
D.2
3.如图,在平面直角坐标系中,以点O为位似中心,将△OCD放大得到△OAB,点C,D的坐标分别为(2,1),(2,0),且△OCD与△OAB的面积之比为1∶4,则点A的坐标为( )
2743835107950A.(8,4)
B.(8,2)
C.(4,2)
D.(4,8)
4.如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1∶,点A的坐标为(1,0),则E点的坐标为( )
2652395178435A.(,0)
B.(,)
C.(,)
D.(2,2)
5.某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则大鱼上的一点(a,b)对应小鱼上的点的坐标是
6.如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.
7.如图,在平面直角坐标系中,作出五边形ABCDE的位似图形,使得新图形A1B1C1D1E1与原图形对应线段的比为2∶1,位似中心是坐标原点O.
8.在平面直角坐标系中,点C,D的坐标分别为C(2,3),D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为
9.在平面直角坐标系中,点P(m,n)是线段AB上一点,以原点O为位似中心,把△AOB放大到原来的两倍,则点P的对应点的坐标为( )
A.(2m,2n) B.(2m,2n)或(-2m,-2n)
C.(m,n) D.(m,n)或(-m,-n)
257619561023510.如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(-1,2)
B.(-9,18)
C.(-9,18)或(9,-18)
D.(-1,2)或(1,-2)
11.如图,原点O是△ABC和△A′B′C′的位似中心,点A(1,0)与A′(-2,0)是对应点,△ABC的面积是,则△A′B′C′的面积是 .
12.如图,网格中每个小正方形的边长为1,已知△ABC,画出△ABC以坐标原点O为位似中心的位似图形△A′B′C′,使△A′B′C′在第三象限,与△ABC的位似比为,写出三角形各顶点的坐标,位似变换后对应顶点的坐标发生了什么变化?
13.如图,正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn,如图位置依次摆放,已知点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
(1)写出正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心的坐标;
(2)正方形A4A5B4C4四个顶点的坐标.
14.如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)求△A1B1C1与△A2B2C2的面积比,即S△A1B1C1∶S△A2B2C2=1∶4.(不写解答过程,直接写出结果)
参考答案:
27.3 位似
第1课时 位似图形的概念及画法
1.D
2.D
3.A
4.A
5.C
6.=.
7.4.
解:如图所示.
8.解:图略.
9.
解:如图所示.
10.D
11.A
12.B
13.
解:(1)位似中心O的位置如图所示.
(2)∵=,
∴△ABC与△A′B′C′的相似比为1∶2.
(3)如图所示.
14.解:(1)证明:∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴======,
∠AB′C′=∠ABC,∠AC′B′=∠ACB,∠AC′D′=∠ACD,∠AD′C′=∠ADC,∠AD′E′=∠ADE,∠AE′D′=∠AED.
∴∠AC′B′+∠AC′D′=∠ACB+∠ACD,
∠AD′C′+∠AD′E′=∠ADC+∠ADE,
即∠B′C′D′=∠BCD,∠C′D′E′=∠CDE.
∵=,∠B′AE′=∠BAE,
∴△B′AE′∽△BAE.
∴=,∠AE′B′=∠AEB,∠AB′E′=∠ABE.
∴===,
∠AB′C′-∠AB′E′=∠ABC-∠ABE,
∠AE′D′-∠AE′B′=∠AED-∠AEB,
即∠E′B′C′=∠EBC,∠B′E′D′=∠BED.
∴四边形BCDE与四边形B′C′D′E′是相似图形.
又∵四边形BCDE与四边形B′C′D′E′对应顶点相交于一点A,
∴四边形BCDE位似于四边形B′C′D′E′.
(2)∵=3,∴=.
∴四边形BCDE与四边形B′C′D′E′位似之比为.
∵S四边形BCDE=20,
∴S四边形B′C′D′E′==20×=.
第2课时 平面直角坐标系中的位似
1.C
2.A
3.C
4.C
5. (-0.5a,-0.5b).
6.解:∵点B的坐标是(4,0),点D的坐标是(6,0),
∴OB=4,OD=6.
∴==.
∵△OAB与△OCD关于点O位似,
∴△OAB与△OCD的相似比为.
7.
解:如图所示.
(4,6)或(-4,-6).
9.B
10.D
11. 6.
12.
解:△ABC三个顶点的坐标分别是A(2,2),B(6,4),C(4,6).△A′B′C′三个顶点的坐标分别是A′(-1,-1),B′(-3,-2),C′(-2,-3).观察图形可知,△A′B′C′各顶点的坐标分别是将△ABC各对应顶点的坐标乘-.
13.解:(1)正方形A1A2B1C1,A2A3B2C2,A3A4B3C3,…,AnAn+1BnCn的位似中心的坐标为(0,0).
(2)∵点C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0),
∴OA1=A1C1=1,OA2=A2C2=2.
∴A3O=A3C3=4.
∴OA4=A4C4=8.∴OA5=16.
∴A4(8,0),A5(16,0),B4(16,8),C4(8,8).
14.
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
