冀教版七年级数学下册第七章相交线与平行线单元测试题(word版含答案)
文档属性
| 名称 | 冀教版七年级数学下册第七章相交线与平行线单元测试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 184.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 12:37:13 | ||
图片预览



文档简介
第七章
相交线与平行线
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列命题是真命题的是
( )
A.在同一平面内,经过一点有且只有一条直线和已知直线垂直
B.在同一平面内,两条直线不是垂直就是平行
C.若a=b,则a+c=b+d
D.两条直线被第三条直线所截,同位角相等
2.如图,把一个三角形纸板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'为( )
A.2
B.4
C.5
D.10
第2题图 第3题图 第4题图
3.下列说法错误的是
( )
A.∠1与∠A是同旁内角
B.∠3与∠A是同位角
C.∠2与∠3是同位角
D.∠3与∠B是内错角
4.如图,下列推理所注理由正确的是
( )
A.因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行)
B.因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等)
C.因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等)
D.因为∠DEC+∠C=180°,所以DE∥BC(同旁内角相等,两直线平行)
5.如图,直线AB,CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为
( )
A.149°
B.121°
C.95°
D.31°
第5题图
第6题图 第7题图
6.如图,根据下列条件,不能判定AB∥DF的是
( )
A.∠A+∠2=180°
B.∠A=∠3
C.∠1=∠4
D.∠1=∠A
7.如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC
∶∠EOD=2∶3,∠BOD=
( )
A.72°
B.56°
C.36°
D.24°
8.如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的线段是
( )
A.AB∥CD∥EF
B.CD∥EF
C.AB∥EF
D.AB∥CD∥EF,BC∥DE
第8题图 第9题图 第10题图
9.如图,直线l1∥l2,且分别与直线l交于C,D两点,把一个含30°角的三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为
( )
A.92°
B.98°
C.102°
D.108°
10.如图,某河水流向经过B,C,D三点,水流三次拐弯后与原来方向相同.若∠ABC=120°,∠BCD=80°,则∠CDE等于
( )
A.20°
B.40°
C.60°
D.80°
11.如图,三角形ABC沿着直线BC向右平移得到三角形A'B'C',点P是直线AA'上任意一点,若三角形ABC,三角形PB'C'的面积分别为S1,S2,则下列关系正确的是
( )
A.S1>S2
B.S1C.S1=S2
D.S1=2S2
第11题图 第12题图
12.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,给出下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB.其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共4小题,每小题3分,共12分)
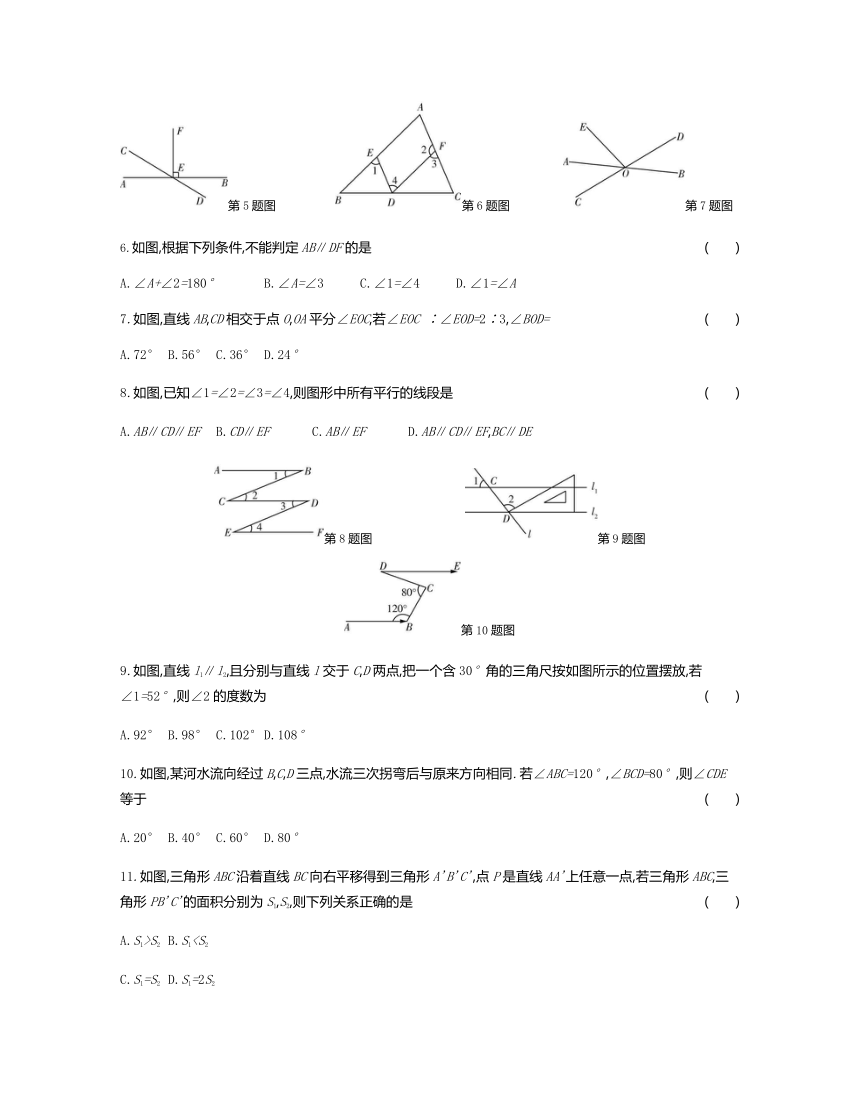
13.如图,在三角形ABC中,∠BCA=90°,BC=3,AC=4,AB=5,点P是线段AB上的一动点,则线段CP的最小值是 .?
第13题图 第14题图 第15题图 第16题图
14.如图,将对边平行的纸带折叠,已知∠1=52°,则∠α= .?
15.如图,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC,则∠C的度数为 .?
16.如图,已知∠ABC=40°,点D为∠ABC内部的一点,以D为顶点,作∠EDF,使得DE∥BC,DF∥AB,则得到的∠EDF= .?
三、解答题(本大题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分6
分)
如图,两直线AB,CD相交于点O,OE平分∠BOD,OF⊥OE,如果∠AOC∶∠AOD=7∶11.求∠COF的度数.
18.(本小题满分8分)
如图,∠1和∠2互补,∠C=∠EDF.
(1)DF与EC的关系为 ;?
(2)试判断DE与BC的关系,并说明理由;
(3)试判断∠DEC与∠DFC的关系,并说明理由.
19.(本小题满分8分)
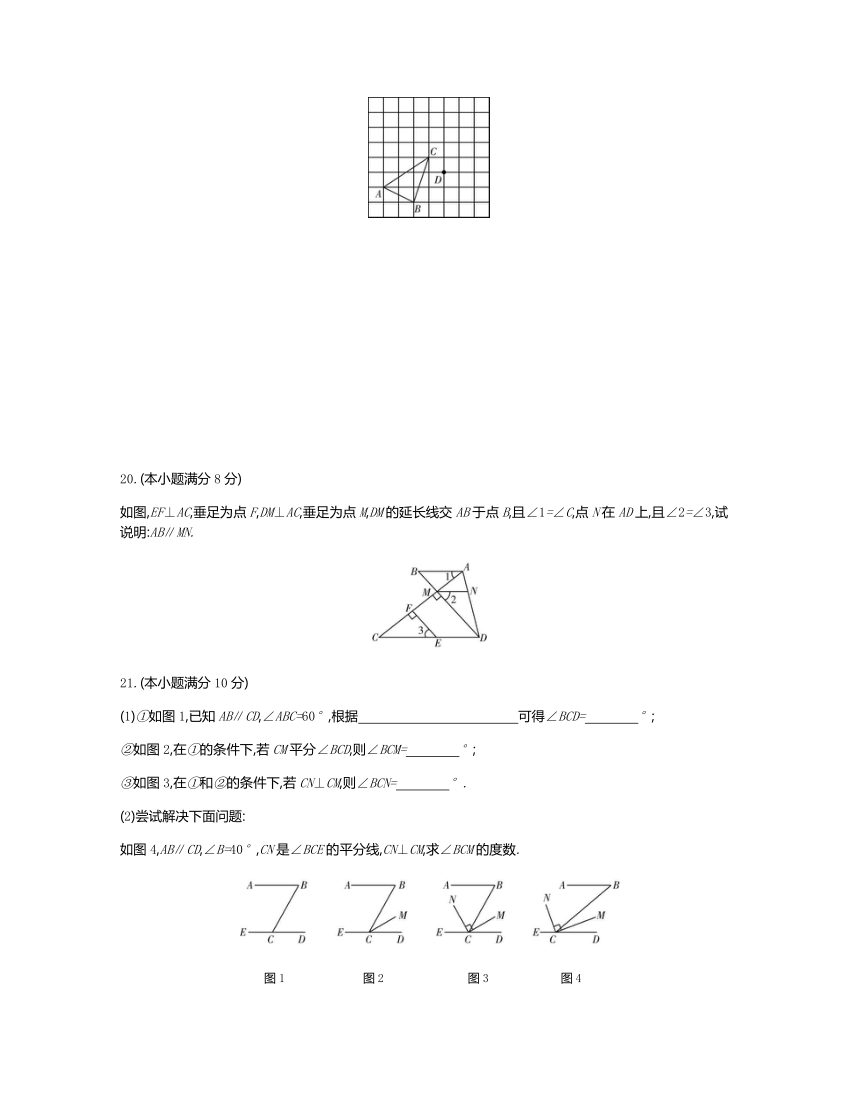
在正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的三个顶点的位置如图所示,将三角形ABC平移后得三角形DEF,使点A的对应点为点D,点B的对应点为点E.
(1)画出三角形DEF;
(2)连接AD,BE,则线段AD与BE的数量关系与位置关系是 ;?
(3)求三角形DEF的面积.
20.(本小题满分8分)
如图,EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明:AB∥MN.
21.(本小题满分10分)
(1)①如图1,已知AB∥CD,∠ABC=60°,根据 可得∠BCD= °;?
②如图2,在①的条件下,若CM平分∠BCD,则∠BCM= °;?
③如图3,在①和②的条件下,若CN⊥CM,则∠BCN= °.?
(2)尝试解决下面问题:
如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
图1
图2 图3 图4
22.(本小题满分12分)
探索:
嘉嘉和琪琪在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:
(1)在图1中,嘉嘉和琪琪都发现:∠APC=∠A+∠C.
嘉嘉的理由是:过点P作PQ∥AB,点Q在点P的左侧,
∴∠APQ=∠A( ).?
∵PQ∥AB,AB∥CD,
∴PQ∥CD( ),?
∴∠CPQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
琪琪的理由是:过点P作PQ∥AB∥CD,点Q在点P的左侧,
∴∠APQ=∠A,∠CPQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面说理过程的横线上,填写依据;两人的说理过程中,完全正确的是 .?
应用:
(2)①在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;?
②在图3中,若∠A=30°,∠C=70°,则∠P的度数为 .?
拓展:
(3)在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
C
A
D
C
D
B
A
C
B
13. 14.64° 15.50° 16.40°或140°
17. 设∠AOC=7x,则∠AOD=11x,
因为∠AOC+∠AOD=180°,所以7x+11x=180°,所以x=10°,
所以∠AOC=70°,∠AOD=110°,所以∠BOD=70°.
因为OE平分∠BOD,所以∠DOE=35°.
因为OE⊥OF,所以∠EOF=90°,
所以∠DOF=90°-35°=55°,
所以∠COF=180°-55°=125°.
18. (1)DF∥EC
(2)DE∥BC.理由如下:
因为DF∥EC,所以∠C+∠CFD=180°,
又因为∠C=∠EDF,所以∠EDF+∠DFC=180°,
所以DE∥BC.
(3)∠DEC=∠DFC.理由如下:
因为DE∥BC,DF∥EC,
所以∠DEC+∠C=180°,∠DFC+∠C=180°,
所以∠DEC=∠DFC.
19. (1)如图.
(2)平行且相等
(3)S三角形DEF=3×3-×2×3-×1×2-×1×3=.
20. 因为EF⊥AC,DM⊥AC,
所以∠CFE=∠CMD=90°(垂直定义),
所以EF∥DM(同位角相等,两直线平行),
所以∠3=∠CDM(两直线平行,同位角相等).
因为∠3=∠2(已知),
所以∠2=∠CDM(等量代换),
所以MN∥CD(内错角相等,两直线平行),
所以∠AMN=∠C(两直线平行,同位角相等).
因为∠1=∠C(已知),
所以∠1=∠AMN(等量代换),
所以AB∥MN(内错角相等,两直线平行).
21. (1)①两直线平行,内错角相等 60
②30
③60
(2)因为AB∥CD,所以∠B+∠BCE=180°.
因为∠B=40°,
所以∠BCE=180°-∠B=180°-40°=140°,
又因为CN是∠BCE的平分线,
所以∠BCN=140°÷2=70°.
因为CN⊥CM,所以∠NCM=90°,
所以∠BCM=90°-∠BCN=90°-70°=20°.
22. (1)两直线平行,内错角相等 平行于同一直线的两条直线平行 嘉嘉
(2)①100°
②40°
推理如下:
①如图,过点P作PE∥AB,
所以∠APE+∠A=180°,因为∠A=120°,所以∠APE=60°.
因为PE∥AB,AB∥CD,所以PE∥CD,
所以∠CPE+∠C=180°,又因为∠C=140°,
所以∠CPE=40°,所以∠APC=∠APE+∠CPE=100°.
②如图,过点P作PF∥AB,
所以∠APF=∠A.
因为PF∥AB,AB∥CD,所以PF∥CD,所以∠CPF=∠C,
所以∠CPF-∠APF=∠C-∠A,即∠APC=∠C-∠A=40°.
(3)∠P=∠A-∠C.理由如下:
如图,过点P作PG∥AB,
所以∠APG+∠A=180°,所以∠APG=180°-∠A.
因为PG∥AB,AB∥CD,所以PG∥CD,
所以∠CPG+∠C=180°,所以∠CPG=180°-∠C,
所以∠APC=∠CPG-∠APG=∠A-∠C.
相交线与平行线
一、选择题(本大题共12小题,每小题3分,共36分.每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列命题是真命题的是
( )
A.在同一平面内,经过一点有且只有一条直线和已知直线垂直
B.在同一平面内,两条直线不是垂直就是平行
C.若a=b,则a+c=b+d
D.两条直线被第三条直线所截,同位角相等
2.如图,把一个三角形纸板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'为( )
A.2
B.4
C.5
D.10
第2题图 第3题图 第4题图
3.下列说法错误的是
( )
A.∠1与∠A是同旁内角
B.∠3与∠A是同位角
C.∠2与∠3是同位角
D.∠3与∠B是内错角
4.如图,下列推理所注理由正确的是
( )
A.因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行)
B.因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等)
C.因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等)
D.因为∠DEC+∠C=180°,所以DE∥BC(同旁内角相等,两直线平行)
5.如图,直线AB,CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为
( )
A.149°
B.121°
C.95°
D.31°
第5题图
第6题图 第7题图
6.如图,根据下列条件,不能判定AB∥DF的是
( )
A.∠A+∠2=180°
B.∠A=∠3
C.∠1=∠4
D.∠1=∠A
7.如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC
∶∠EOD=2∶3,∠BOD=
( )
A.72°
B.56°
C.36°
D.24°
8.如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的线段是
( )
A.AB∥CD∥EF
B.CD∥EF
C.AB∥EF
D.AB∥CD∥EF,BC∥DE
第8题图 第9题图 第10题图
9.如图,直线l1∥l2,且分别与直线l交于C,D两点,把一个含30°角的三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为
( )
A.92°
B.98°
C.102°
D.108°
10.如图,某河水流向经过B,C,D三点,水流三次拐弯后与原来方向相同.若∠ABC=120°,∠BCD=80°,则∠CDE等于
( )
A.20°
B.40°
C.60°
D.80°
11.如图,三角形ABC沿着直线BC向右平移得到三角形A'B'C',点P是直线AA'上任意一点,若三角形ABC,三角形PB'C'的面积分别为S1,S2,则下列关系正确的是
( )
A.S1>S2
B.S1
D.S1=2S2
第11题图 第12题图
12.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,给出下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB.其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图,在三角形ABC中,∠BCA=90°,BC=3,AC=4,AB=5,点P是线段AB上的一动点,则线段CP的最小值是 .?
第13题图 第14题图 第15题图 第16题图
14.如图,将对边平行的纸带折叠,已知∠1=52°,则∠α= .?
15.如图,已知∠1=70°,∠2=50°,∠D=70°,AE∥BC,则∠C的度数为 .?
16.如图,已知∠ABC=40°,点D为∠ABC内部的一点,以D为顶点,作∠EDF,使得DE∥BC,DF∥AB,则得到的∠EDF= .?
三、解答题(本大题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分6
分)
如图,两直线AB,CD相交于点O,OE平分∠BOD,OF⊥OE,如果∠AOC∶∠AOD=7∶11.求∠COF的度数.
18.(本小题满分8分)
如图,∠1和∠2互补,∠C=∠EDF.
(1)DF与EC的关系为 ;?
(2)试判断DE与BC的关系,并说明理由;
(3)试判断∠DEC与∠DFC的关系,并说明理由.
19.(本小题满分8分)
在正方形网格中,每个小正方形的边长都为1个单位长度,三角形ABC的三个顶点的位置如图所示,将三角形ABC平移后得三角形DEF,使点A的对应点为点D,点B的对应点为点E.
(1)画出三角形DEF;
(2)连接AD,BE,则线段AD与BE的数量关系与位置关系是 ;?
(3)求三角形DEF的面积.
20.(本小题满分8分)
如图,EF⊥AC,垂足为点F,DM⊥AC,垂足为点M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试说明:AB∥MN.
21.(本小题满分10分)
(1)①如图1,已知AB∥CD,∠ABC=60°,根据 可得∠BCD= °;?
②如图2,在①的条件下,若CM平分∠BCD,则∠BCM= °;?
③如图3,在①和②的条件下,若CN⊥CM,则∠BCN= °.?
(2)尝试解决下面问题:
如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线,CN⊥CM,求∠BCM的度数.
图1
图2 图3 图4
22.(本小题满分12分)
探索:
嘉嘉和琪琪在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:
(1)在图1中,嘉嘉和琪琪都发现:∠APC=∠A+∠C.
嘉嘉的理由是:过点P作PQ∥AB,点Q在点P的左侧,
∴∠APQ=∠A( ).?
∵PQ∥AB,AB∥CD,
∴PQ∥CD( ),?
∴∠CPQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
琪琪的理由是:过点P作PQ∥AB∥CD,点Q在点P的左侧,
∴∠APQ=∠A,∠CPQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面说理过程的横线上,填写依据;两人的说理过程中,完全正确的是 .?
应用:
(2)①在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;?
②在图3中,若∠A=30°,∠C=70°,则∠P的度数为 .?
拓展:
(3)在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
C
A
D
C
D
B
A
C
B
13. 14.64° 15.50° 16.40°或140°
17. 设∠AOC=7x,则∠AOD=11x,
因为∠AOC+∠AOD=180°,所以7x+11x=180°,所以x=10°,
所以∠AOC=70°,∠AOD=110°,所以∠BOD=70°.
因为OE平分∠BOD,所以∠DOE=35°.
因为OE⊥OF,所以∠EOF=90°,
所以∠DOF=90°-35°=55°,
所以∠COF=180°-55°=125°.
18. (1)DF∥EC
(2)DE∥BC.理由如下:
因为DF∥EC,所以∠C+∠CFD=180°,
又因为∠C=∠EDF,所以∠EDF+∠DFC=180°,
所以DE∥BC.
(3)∠DEC=∠DFC.理由如下:
因为DE∥BC,DF∥EC,
所以∠DEC+∠C=180°,∠DFC+∠C=180°,
所以∠DEC=∠DFC.
19. (1)如图.
(2)平行且相等
(3)S三角形DEF=3×3-×2×3-×1×2-×1×3=.
20. 因为EF⊥AC,DM⊥AC,
所以∠CFE=∠CMD=90°(垂直定义),
所以EF∥DM(同位角相等,两直线平行),
所以∠3=∠CDM(两直线平行,同位角相等).
因为∠3=∠2(已知),
所以∠2=∠CDM(等量代换),
所以MN∥CD(内错角相等,两直线平行),
所以∠AMN=∠C(两直线平行,同位角相等).
因为∠1=∠C(已知),
所以∠1=∠AMN(等量代换),
所以AB∥MN(内错角相等,两直线平行).
21. (1)①两直线平行,内错角相等 60
②30
③60
(2)因为AB∥CD,所以∠B+∠BCE=180°.
因为∠B=40°,
所以∠BCE=180°-∠B=180°-40°=140°,
又因为CN是∠BCE的平分线,
所以∠BCN=140°÷2=70°.
因为CN⊥CM,所以∠NCM=90°,
所以∠BCM=90°-∠BCN=90°-70°=20°.
22. (1)两直线平行,内错角相等 平行于同一直线的两条直线平行 嘉嘉
(2)①100°
②40°
推理如下:
①如图,过点P作PE∥AB,
所以∠APE+∠A=180°,因为∠A=120°,所以∠APE=60°.
因为PE∥AB,AB∥CD,所以PE∥CD,
所以∠CPE+∠C=180°,又因为∠C=140°,
所以∠CPE=40°,所以∠APC=∠APE+∠CPE=100°.
②如图,过点P作PF∥AB,
所以∠APF=∠A.
因为PF∥AB,AB∥CD,所以PF∥CD,所以∠CPF=∠C,
所以∠CPF-∠APF=∠C-∠A,即∠APC=∠C-∠A=40°.
(3)∠P=∠A-∠C.理由如下:
如图,过点P作PG∥AB,
所以∠APG+∠A=180°,所以∠APG=180°-∠A.
因为PG∥AB,AB∥CD,所以PG∥CD,
所以∠CPG+∠C=180°,所以∠CPG=180°-∠C,
所以∠APC=∠CPG-∠APG=∠A-∠C.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
