人教版数学九年级上册第二十四章《24.2.2 直线和圆的位置关系》课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册第二十四章《24.2.2 直线和圆的位置关系》课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 965.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
第二十四章
圆的有关性质
人教版数学九年级上册
24.2.2
直线和圆的位置关系
学习目标
1.理解直线与圆有相交、相切、相离三种位置关系.
2.了解切线的概念,探索切线与过切点的直径之间的关系.
3.能判定一条直线是否为圆的切线.
导入新知
观察太阳从海平面升起的情景,把海平面看作一条直线,太阳看作一个圆,由此你能得出直线与圆的位置关系吗?
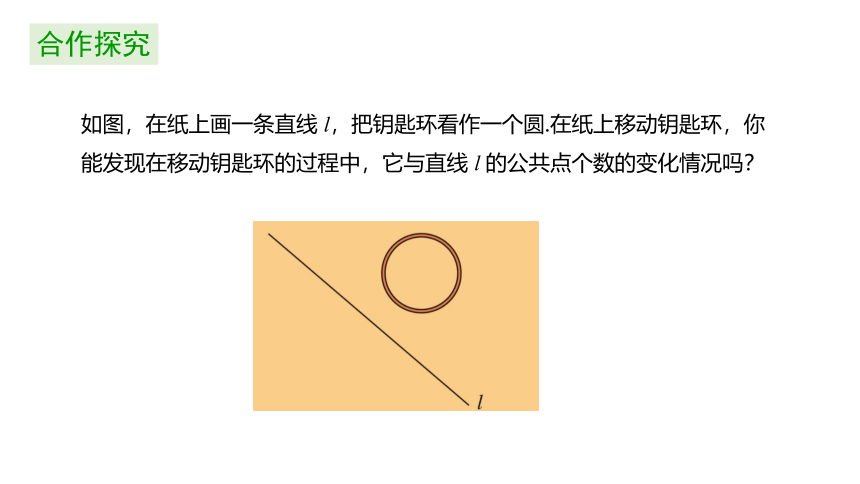
如图,在纸上画一条直线
l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线
l
的公共点个数的变化情况吗?
合作探究
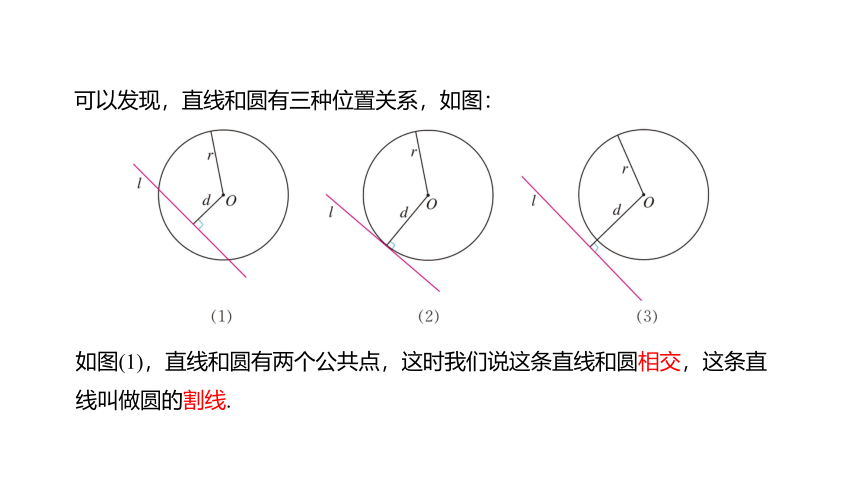
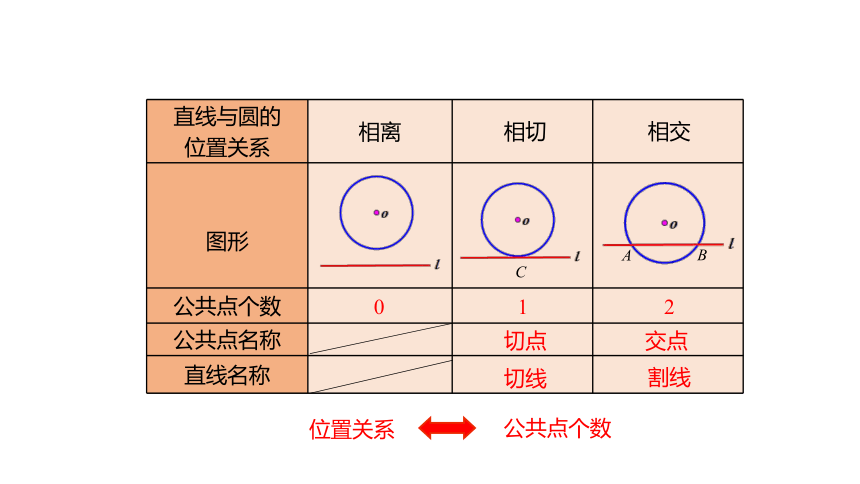
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
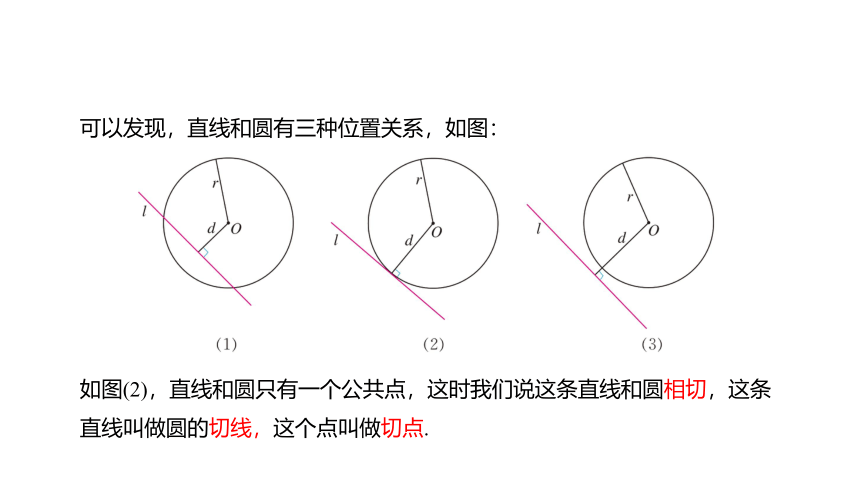
可以发现,直线和圆有三种位置关系,如图:
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
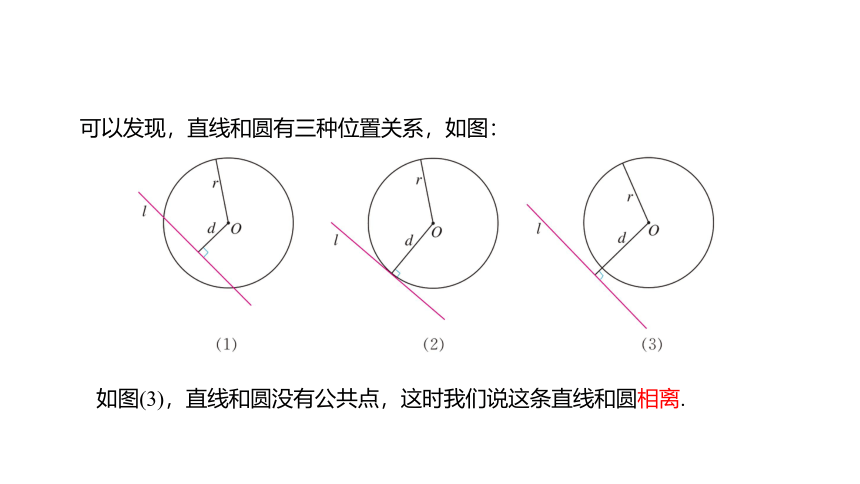
可以发现,直线和圆有三种位置关系,如图:
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2
交点
1
切点
切线
0
相离
相切
相交
位置关系
公共点个数
A
B
C
割线
同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
位置关系
数量关系
用圆心O到直线的距离d与圆的半径r的关系来区分直线与圆的位置关系:
∟
r
d
o
公共点个数
r
d
o
A
B
∟
r
d
o
C
1.判断直线和圆的位置关系有两种方法:
①将圆心到直线的距离与圆的半径相比较;
②根据直线与圆的交点的个数判定.
2.直线与圆相切是一种特殊的位置关系,此时直线与圆只有一个交点.
一个圆有无数条切线,每一条切线与圆都只有一个切点.
已知圆的直径为13
cm,设直线和圆心的距离为d.
(1)
若d
=4.5
cm,则直线与圆
,直线与圆有
个公共点;
(2)
若d
=6.5
cm,则直线与圆
,直线与圆有
个公共点;
(3)
若d
=
8
cm,则直线与圆
,直线与圆有
个公共点.
相交
2
相切
1
相离
0
典型例题
1.已知⊙O的半径为5
cm,圆心O到直线
l
的距离为5cm,则直线
l
与⊙O的位置关系为(
)
B
A.相交
B.相切
C.相离
D.无法确定
课堂练习
2.如图,Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,判断以点C为圆心,下列
r
为半径的⊙C与AB的位置关系:
(1)
r
=2
cm;
(2)
r=2.4
cm;
(3)
r
=3
cm.
?
B
C
A
D
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d相离:0个
相切:1个
相交:2个
归纳新知
1.如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是(
)
C
A.相交
B.相切
C.相交或相切
D.以上都不正确
解:如果直线上一点与一个圆的圆心的距离等于这个圆的半径,
根据垂线段最短,则圆心到直线的距离小于或等于圆的半径,
从而直线和圆相交或相切.
中考实题
2.已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
?
?
如图,已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
O
A
B
x
y
l
D
?
?
?
D
再
见
第二十四章
圆的有关性质
人教版数学九年级上册
24.2.2
直线和圆的位置关系
学习目标
1.理解直线与圆有相交、相切、相离三种位置关系.
2.了解切线的概念,探索切线与过切点的直径之间的关系.
3.能判定一条直线是否为圆的切线.
导入新知
观察太阳从海平面升起的情景,把海平面看作一条直线,太阳看作一个圆,由此你能得出直线与圆的位置关系吗?
如图,在纸上画一条直线
l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线
l
的公共点个数的变化情况吗?
合作探究
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
可以发现,直线和圆有三种位置关系,如图:
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
可以发现,直线和圆有三种位置关系,如图:
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2
交点
1
切点
切线
0
相离
相切
相交
位置关系
公共点个数
A
B
C
割线
同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
直线和圆相交
d<
r
直线和圆相切
d=
r
直线和圆相离
d>
r
位置关系
数量关系
用圆心O到直线的距离d与圆的半径r的关系来区分直线与圆的位置关系:
∟
r
d
o
公共点个数
r
d
o
A
B
∟
r
d
o
C
1.判断直线和圆的位置关系有两种方法:
①将圆心到直线的距离与圆的半径相比较;
②根据直线与圆的交点的个数判定.
2.直线与圆相切是一种特殊的位置关系,此时直线与圆只有一个交点.
一个圆有无数条切线,每一条切线与圆都只有一个切点.
已知圆的直径为13
cm,设直线和圆心的距离为d.
(1)
若d
=4.5
cm,则直线与圆
,直线与圆有
个公共点;
(2)
若d
=6.5
cm,则直线与圆
,直线与圆有
个公共点;
(3)
若d
=
8
cm,则直线与圆
,直线与圆有
个公共点.
相交
2
相切
1
相离
0
典型例题
1.已知⊙O的半径为5
cm,圆心O到直线
l
的距离为5cm,则直线
l
与⊙O的位置关系为(
)
B
A.相交
B.相切
C.相离
D.无法确定
课堂练习
2.如图,Rt△ABC中,∠C=90°,AC=3
cm,BC=4
cm,判断以点C为圆心,下列
r
为半径的⊙C与AB的位置关系:
(1)
r
=2
cm;
(2)
r=2.4
cm;
(3)
r
=3
cm.
?
B
C
A
D
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
相切:1个
相交:2个
归纳新知
1.如果直线上一点与一个圆的圆心的距离等于这个圆的半径,那么这条直线与这个圆的位置关系是(
)
C
A.相交
B.相切
C.相交或相切
D.以上都不正确
解:如果直线上一点与一个圆的圆心的距离等于这个圆的半径,
根据垂线段最短,则圆心到直线的距离小于或等于圆的半径,
从而直线和圆相交或相切.
中考实题
2.已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
?
?
如图,已知直线
y=
kx(k≠0)
经过点(12,
-5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点)
,则m的取值范围为
.
O
A
B
x
y
l
D
?
?
?
D
再
见
同课章节目录
