沪教版(上海)数学八年级第二学期-22.4 梯形复习课 教案
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.4 梯形复习课 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 121.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
梯形复习课
教学目标
1、了解梯形的定义以及分类;
2.掌握等腰梯形的性质定理、判定定理,并能应用这些定理进行计算和证明;
3.会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题;
4.提高探索等腰梯形性质的活动能力,提高类比、归纳能力,感受类比、分类讨论和转化等数学思想和方法在解决问题中的作用.
教学重点及难点
掌握等腰梯形的判定定理、并能应用这些定理进行计算和证明;
会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题
教学过程设计
一、知识梳理
1.什么样的四边形叫梯形,什么样的梯形是直角梯形、等腰梯形?
(1)一组对边平行而另一组对边不平行的四边形叫做梯形.
(2)直角梯形:有一个内角是直角的梯形.
(3)等腰梯形:两腰相等的梯形.
2.等腰梯形有哪些性质?
(1)
等腰梯形在同一底上的两个角相等;
(2)等腰梯形的两条对角线相等.
(3)等腰梯形是轴对称图形,但不是中心对称图形.
3.等腰梯形有哪些判定方法?
(1)定义法
(2)在同一底上的两个角相等的梯形是等腰梯形.
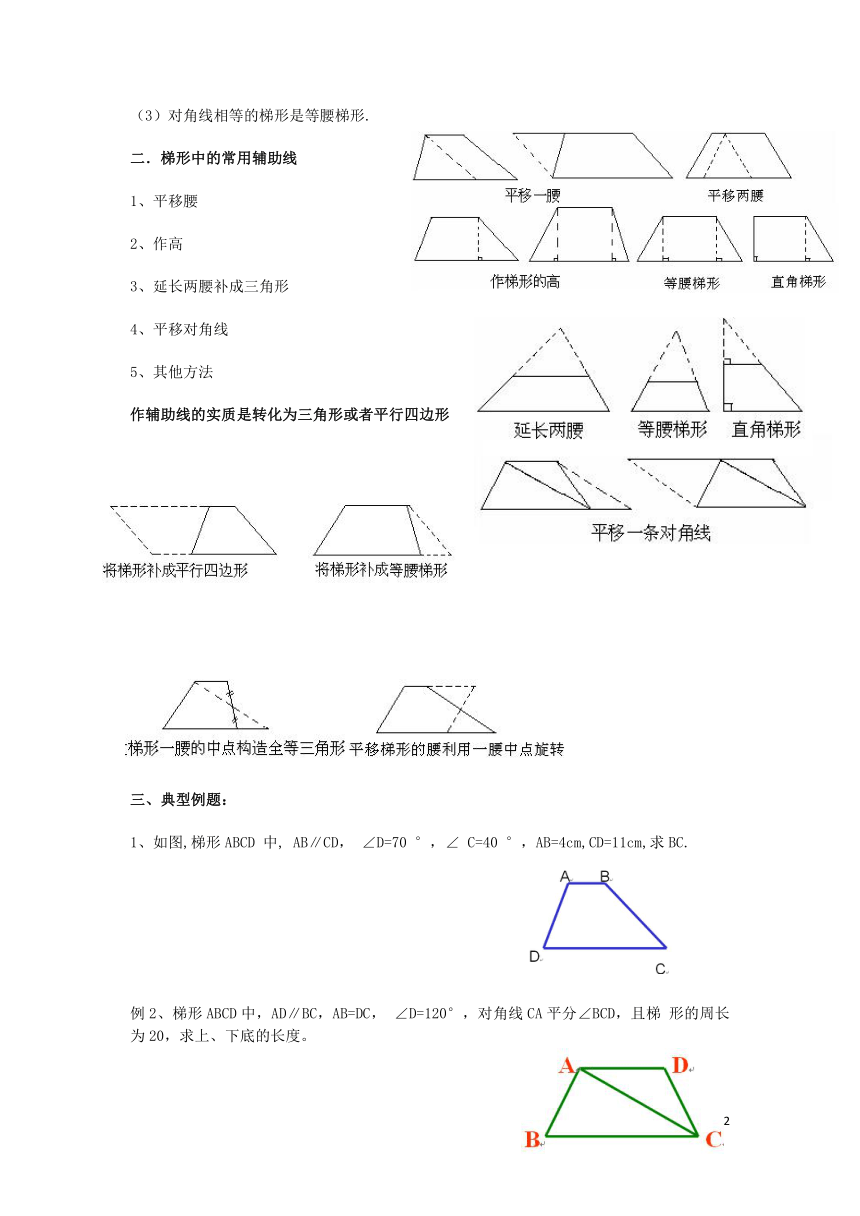
(3)对角线相等的梯形是等腰梯形.
二.梯形中的常用辅助线
1、平移腰
2、作高
3、延长两腰补成三角形
4、平移对角线
5、其他方法
作辅助线的实质是转化为三角形或者平行四边形
三、典型例题:
1、如图,梯形ABCD
中,
AB∥CD,
∠D=70
°,∠
C=40
°,AB=4cm,CD=11cm,求BC.
例2、梯形ABCD中,AD∥BC,AB=DC,
∠D=120°,对角线CA平分∠BCD,且梯
形的周长为20,求上、下底的长度。
例3.梯形ABCD中,AD∥BC,AB=DC,对角线
AC⊥BD,DE⊥BC于E,ED=10.求AD+BC的值.
例4、如图,梯形ABCD中,AD
∥BC,E是CD的中点,EF⊥AB于点F,AB=6cm,EF=5cm,试求梯形ABCD的面积
四、巩固练习
1、已知四边形ABCD各个内角度数的比为∠A∶∠B∶∠C∶∠D
=2∶2∶1∶3,则此四边形是_________.
2、已知梯形的两底长分别是6,8,一腰长为7。则另一腰长a的取值范围是_________
,
若a为奇数,则此梯形为______梯形。
3、等腰梯形有一个角为120°,腰长为3cm,一底边长为4cm,
则另一底边长为_________.
4、等腰梯形ABCD中,AD∥BC,AB=CD,AD:BC=5:6,∠A与∠D的平分线与BC的交点分BC为三等分,梯形周长57,求梯形的上下底的长.
五、思考探究题.
已知:如图,梯形ABCD中,AD∥BC,∠A=90°,∠C=45°,AB=AD=4.E是直线AD上一点,连接BE,过点E作EF⊥BE交直线CD于点F.连接BF.
(1)若点E是线段AD上一点(与点A、D不重合),(如图1所示)求证:BE=EF.
(2)若△BEF的面积是,请直接写出DE的长;
(1)证明:如图1,在AB上截取AG=AE,连接EG,则∠AGE=∠AEG.
∵∠A=90°,∠A+∠AGE+∠AEG=180°,
∴∠AGE=45°.
∴∠BGE=135°.
∵AD∥BC,
∴∠C+∠D=180°.
又∵∠C=45°,
∴∠D=135°,
∴∠BGE=∠D.
∵AB=AD,AG=AE,
∴BG=DE.
∵EF⊥BE,
∴∠BEF=90°.
又∵∠A+∠ABE+∠AEB=180°,
∠AEB+∠BEF+∠DEF=180°,
∠A=90°,
∴∠ABE=∠DEF.
在△BGE与△EDF中,
,
∴△BGE≌△EDF(ASA),
∴BE=EF;
(2)解:△BEF的面积是BE?EF=BE2
Ⅰ)当点E在线段AD上时,如图1.
Ⅱ)当点E在线段AD延长线上时,如图2,延长AB到G,使BG=DE,连接EG,则△AGE为等腰直角三角形.
∵AE∥BC,
∴∠EBC=∠AEB,
∴∠EBC+90°=∠AEB+90°,即∠GBE=∠DEF.
在△BGE与△EDF中,
,
∴△BGE≌△EDF(ASA),
∴BE=EF.
,矛盾,则DE不存在
Ⅲ)当点E在线段DA延长线上时,如图3,
延长BA到G,使BG=DE,连接EG,则△AGE为等腰直角三角形.
在△BGE与△EDF中,
,
∴△BGE≌△EDF(ASA),
∴BE=EF.
综上所述,此时DE的长为3或5
六、课堂小结
七、布置作业
5
教学目标
1、了解梯形的定义以及分类;
2.掌握等腰梯形的性质定理、判定定理,并能应用这些定理进行计算和证明;
3.会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题;
4.提高探索等腰梯形性质的活动能力,提高类比、归纳能力,感受类比、分类讨论和转化等数学思想和方法在解决问题中的作用.
教学重点及难点
掌握等腰梯形的判定定理、并能应用这些定理进行计算和证明;
会添加适当的辅助线,将等腰梯形问题转化成三角形、平行四边形等熟知的几何图形来解决问题
教学过程设计
一、知识梳理
1.什么样的四边形叫梯形,什么样的梯形是直角梯形、等腰梯形?
(1)一组对边平行而另一组对边不平行的四边形叫做梯形.
(2)直角梯形:有一个内角是直角的梯形.
(3)等腰梯形:两腰相等的梯形.
2.等腰梯形有哪些性质?
(1)
等腰梯形在同一底上的两个角相等;
(2)等腰梯形的两条对角线相等.
(3)等腰梯形是轴对称图形,但不是中心对称图形.
3.等腰梯形有哪些判定方法?
(1)定义法
(2)在同一底上的两个角相等的梯形是等腰梯形.
(3)对角线相等的梯形是等腰梯形.
二.梯形中的常用辅助线
1、平移腰
2、作高
3、延长两腰补成三角形
4、平移对角线
5、其他方法
作辅助线的实质是转化为三角形或者平行四边形
三、典型例题:
1、如图,梯形ABCD
中,
AB∥CD,
∠D=70
°,∠
C=40
°,AB=4cm,CD=11cm,求BC.
例2、梯形ABCD中,AD∥BC,AB=DC,
∠D=120°,对角线CA平分∠BCD,且梯
形的周长为20,求上、下底的长度。
例3.梯形ABCD中,AD∥BC,AB=DC,对角线
AC⊥BD,DE⊥BC于E,ED=10.求AD+BC的值.
例4、如图,梯形ABCD中,AD
∥BC,E是CD的中点,EF⊥AB于点F,AB=6cm,EF=5cm,试求梯形ABCD的面积
四、巩固练习
1、已知四边形ABCD各个内角度数的比为∠A∶∠B∶∠C∶∠D
=2∶2∶1∶3,则此四边形是_________.
2、已知梯形的两底长分别是6,8,一腰长为7。则另一腰长a的取值范围是_________
,
若a为奇数,则此梯形为______梯形。
3、等腰梯形有一个角为120°,腰长为3cm,一底边长为4cm,
则另一底边长为_________.
4、等腰梯形ABCD中,AD∥BC,AB=CD,AD:BC=5:6,∠A与∠D的平分线与BC的交点分BC为三等分,梯形周长57,求梯形的上下底的长.
五、思考探究题.
已知:如图,梯形ABCD中,AD∥BC,∠A=90°,∠C=45°,AB=AD=4.E是直线AD上一点,连接BE,过点E作EF⊥BE交直线CD于点F.连接BF.
(1)若点E是线段AD上一点(与点A、D不重合),(如图1所示)求证:BE=EF.
(2)若△BEF的面积是,请直接写出DE的长;
(1)证明:如图1,在AB上截取AG=AE,连接EG,则∠AGE=∠AEG.
∵∠A=90°,∠A+∠AGE+∠AEG=180°,
∴∠AGE=45°.
∴∠BGE=135°.
∵AD∥BC,
∴∠C+∠D=180°.
又∵∠C=45°,
∴∠D=135°,
∴∠BGE=∠D.
∵AB=AD,AG=AE,
∴BG=DE.
∵EF⊥BE,
∴∠BEF=90°.
又∵∠A+∠ABE+∠AEB=180°,
∠AEB+∠BEF+∠DEF=180°,
∠A=90°,
∴∠ABE=∠DEF.
在△BGE与△EDF中,
,
∴△BGE≌△EDF(ASA),
∴BE=EF;
(2)解:△BEF的面积是BE?EF=BE2
Ⅰ)当点E在线段AD上时,如图1.
Ⅱ)当点E在线段AD延长线上时,如图2,延长AB到G,使BG=DE,连接EG,则△AGE为等腰直角三角形.
∵AE∥BC,
∴∠EBC=∠AEB,
∴∠EBC+90°=∠AEB+90°,即∠GBE=∠DEF.
在△BGE与△EDF中,
,
∴△BGE≌△EDF(ASA),
∴BE=EF.
,矛盾,则DE不存在
Ⅲ)当点E在线段DA延长线上时,如图3,
延长BA到G,使BG=DE,连接EG,则△AGE为等腰直角三角形.
在△BGE与△EDF中,
,
∴△BGE≌△EDF(ASA),
∴BE=EF.
综上所述,此时DE的长为3或5
六、课堂小结
七、布置作业
5
