人教版数学七年级下册5.1.2垂线同步练习 (Word版,含答案)
文档属性
| 名称 | 人教版数学七年级下册5.1.2垂线同步练习 (Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 430.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览


文档简介
人教版数学七下5.1.2
《垂线》同步练习
一、选择题
1.下列选项中,过点P画AB的垂线CD,三角尺放法正确的是(
)
2.在同一平面内,下列语句正确的是(
)
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.两直线相交,则一定垂直
3.如图,点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为(
)
A.35°
B.45°
C.55°
D.65°
4.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是(
)
A.两点确定一条直线
B.经过一点有且只有一条直线与已知直线垂直
C.过一点只能作一条直线
D.垂线段最短
5.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有(
)
A.2条
B.3条
C.4条
D.5条
6.如图,已知直线AB,CD互相垂直,垂足为O
,直线EF过点O,∠DOF∶∠BOF=2∶3,则∠AOE的度数为( )
A.36°
B.54°
C.
48°
D.42°
7.下列说法中错误的是( )
A.两直线相交,若有一组邻补角相等,则这两条直线垂直
B.两直线相交,若有两个角相等,则这两条直线垂直
C.两直线相交,若有一组对顶角互补,则这两条直线垂直
D.两直线相交,若有三个角相等,则这两条直线垂直
8.如图,已知AB⊥BD,BC⊥CD,AD=a,CD=b,则BD的长的取值范围为(
)
A.大于b
B.小于a
C.大于b且小于a
D.无法确定
9.如图,有三条公路,其中AC与AB垂直,小明和小亮分别沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是(
)
A.小亮骑车的速度快
B.小明骑车的速度快
C.两人一样快
D.因为不知道公路的长度,所以无法判断他们速度的快慢
10.P为直线m外一点,A,B,C为直线m上三点,PA=4
cm,PB=5
cm,PC=2
cm,则点P到直线m的距离( )
A.等于4
cm
B.等于2
cm
C.小于2
cm
D.不大于2
cm
二、填空题
11.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向是_______.
12.如图所示,OA⊥OC,∠1=∠2,则OB与OD的位置关系是____________.
13.如图所示,AC⊥l1,AB⊥l2,垂足分别为A,B,则A点到直线l2的距离是线段____的长,线段AC的长是点____到直线____的距离.
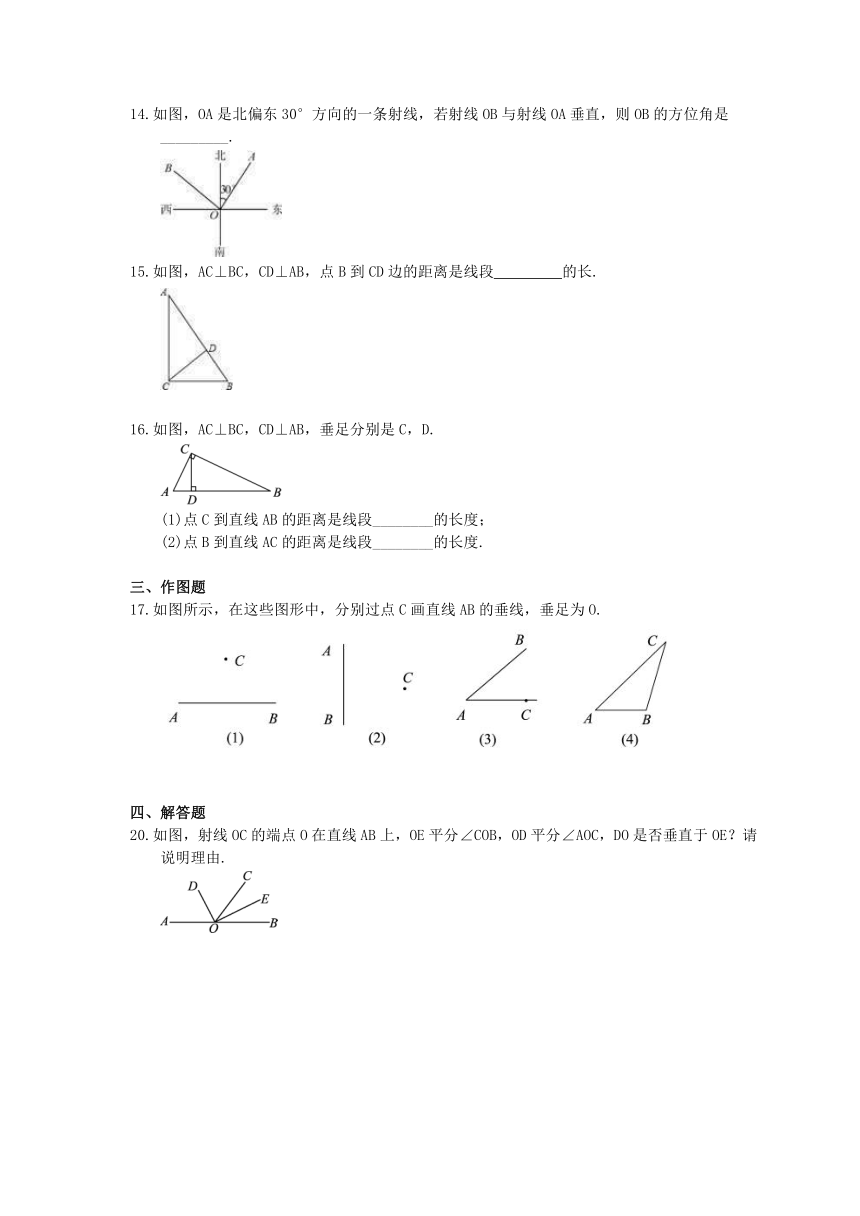
14.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是_________.
15.如图,AC⊥BC,CD⊥AB,点B到CD边的距离是线段
的长.
16.如图,AC⊥BC,CD⊥AB,垂足分别是C,D.
(1)点C到直线AB的距离是线段________的长度;
(2)点B到直线AC的距离是线段________的长度.
三、作图题
17.如图所示,在这些图形中,分别过点C画直线AB的垂线,垂足为O.
四、解答题
20.如图,射线OC的端点O在直线AB上,OE平分∠COB,OD平分∠AOC,DO是否垂直于OE?请说明理由.
21.如图,直线AB,CD相交于点O,OM⊥AB,NO⊥CD.
(1)若∠1=∠2,求∠AOD的度数;
(2)若∠1=∠BOC,求∠2和∠MOD的度数.
22.如图,已知AO⊥CO,∠COD=40°,∠BOC=∠AOD.试说明OB⊥OD.
请完善解答过程,并在括号内填上相应的依据:
解:因为AO⊥CO,
所以∠AOC=__________(________________________).
又因为∠COD=40°(已知),
所以∠AOD=________.
又因为∠BOC=∠AOD(已知),
所以∠BOC=________(__________),
所以∠BOD=________,
所以________⊥________(____________).
23.如图,直线AB与CD相交于点O,OE,OF分别是∠BOD,∠AOD的平分线.
(1)∠DOE的补角是__________________;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由.
24.如图,O是直线AB上一点,OE,OC,OF是射线,OE⊥OF,若∠BOC=2∠COE,∠AOF的度数比∠COE的度数的4倍小8°.求∠COE的度数.
参考答案
答案为:C
答案为:C
答案为:C
答案为:B
答案为:D
答案为:B
答案为:B
答案为:C
答案为:A
答案为:D
答案为:北偏西60°
答案为:OB⊥OD
答案为:AB
C
l1
答案为:北偏西60°
答案为:BD
答案为:(1)CD (2)BC
解:如图所示.
解:DO⊥OE.理由:
因为OE平分∠COB,
所以∠COE=∠COB.
因为OD平分∠AOC,
所以∠DOC=∠AOC,
所以∠DOE=∠COE+∠DOC=∠COB+∠AOC=(∠COB+∠AOC)=∠AOB.
因为∠AOB是平角,
所以∠DOE=×180°=90°,
所以DO⊥OE.
解:∵OM⊥AB,NO⊥CD,
∴∠BOM=∠AOM=∠NOD=∠CON=90°.
(1)∵∠1=∠2,∴∠1=∠2=45°,
∴∠AOD=180°-∠2=180°-45°=135°,
即∠AOD的度数是135°.
(2)∵∠1+∠BOM=∠BOC,∠1=∠BOC,
∴∠1=∠BOM=30°,∴∠2=90°-∠1=60°.
∵∠1+∠MOD=∠COD=180°,
∴∠MOD=180°-∠1=150°.
90° 垂直的定义 50° 50° 等量代换 90°
OB OD 垂直的定义
(1)
∠AOE或∠COE
解:(1)因为OE是∠BOD的平分线,
所以∠DOE=∠BOE,
又因为∠BOE+∠AOE=180°,∠DOE+∠COE=180°,
所以∠DOE的补角是∠AOE或∠COE
(2)因为OE是∠BOD的平分线,∠BOD=62°,
所以∠BOE=∠BOD=31°,
所以∠AOE=180°-31°=149°,
因为∠BOD=62°,所以∠AOD=180°-62°=118°,
因为OF是∠AOD的平分线,
所以∠DOF=×118°=59°
(3)OE与OF的位置关系是OE⊥OF.理由如下:
因为OE,OF分别是∠BOD,∠AOD的平分线,
所以∠DOE=∠BOD,∠DOF=∠AOD,
因为∠BOD+∠AOD=180°,
所以∠EOF=∠DOE+∠DOF=(∠BOD+∠AOD)=90°,
所以OE⊥OF.
答案为:14°.
《垂线》同步练习
一、选择题
1.下列选项中,过点P画AB的垂线CD,三角尺放法正确的是(
)
2.在同一平面内,下列语句正确的是(
)
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.两直线相交,则一定垂直
3.如图,点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为(
)
A.35°
B.45°
C.55°
D.65°
4.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是(
)
A.两点确定一条直线
B.经过一点有且只有一条直线与已知直线垂直
C.过一点只能作一条直线
D.垂线段最短
5.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有(
)
A.2条
B.3条
C.4条
D.5条
6.如图,已知直线AB,CD互相垂直,垂足为O
,直线EF过点O,∠DOF∶∠BOF=2∶3,则∠AOE的度数为( )
A.36°
B.54°
C.
48°
D.42°
7.下列说法中错误的是( )
A.两直线相交,若有一组邻补角相等,则这两条直线垂直
B.两直线相交,若有两个角相等,则这两条直线垂直
C.两直线相交,若有一组对顶角互补,则这两条直线垂直
D.两直线相交,若有三个角相等,则这两条直线垂直
8.如图,已知AB⊥BD,BC⊥CD,AD=a,CD=b,则BD的长的取值范围为(
)
A.大于b
B.小于a
C.大于b且小于a
D.无法确定
9.如图,有三条公路,其中AC与AB垂直,小明和小亮分别沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是(
)
A.小亮骑车的速度快
B.小明骑车的速度快
C.两人一样快
D.因为不知道公路的长度,所以无法判断他们速度的快慢
10.P为直线m外一点,A,B,C为直线m上三点,PA=4
cm,PB=5
cm,PC=2
cm,则点P到直线m的距离( )
A.等于4
cm
B.等于2
cm
C.小于2
cm
D.不大于2
cm
二、填空题
11.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方向是_______.
12.如图所示,OA⊥OC,∠1=∠2,则OB与OD的位置关系是____________.
13.如图所示,AC⊥l1,AB⊥l2,垂足分别为A,B,则A点到直线l2的距离是线段____的长,线段AC的长是点____到直线____的距离.
14.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是_________.
15.如图,AC⊥BC,CD⊥AB,点B到CD边的距离是线段
的长.
16.如图,AC⊥BC,CD⊥AB,垂足分别是C,D.
(1)点C到直线AB的距离是线段________的长度;
(2)点B到直线AC的距离是线段________的长度.
三、作图题
17.如图所示,在这些图形中,分别过点C画直线AB的垂线,垂足为O.
四、解答题
20.如图,射线OC的端点O在直线AB上,OE平分∠COB,OD平分∠AOC,DO是否垂直于OE?请说明理由.
21.如图,直线AB,CD相交于点O,OM⊥AB,NO⊥CD.
(1)若∠1=∠2,求∠AOD的度数;
(2)若∠1=∠BOC,求∠2和∠MOD的度数.
22.如图,已知AO⊥CO,∠COD=40°,∠BOC=∠AOD.试说明OB⊥OD.
请完善解答过程,并在括号内填上相应的依据:
解:因为AO⊥CO,
所以∠AOC=__________(________________________).
又因为∠COD=40°(已知),
所以∠AOD=________.
又因为∠BOC=∠AOD(已知),
所以∠BOC=________(__________),
所以∠BOD=________,
所以________⊥________(____________).
23.如图,直线AB与CD相交于点O,OE,OF分别是∠BOD,∠AOD的平分线.
(1)∠DOE的补角是__________________;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由.
24.如图,O是直线AB上一点,OE,OC,OF是射线,OE⊥OF,若∠BOC=2∠COE,∠AOF的度数比∠COE的度数的4倍小8°.求∠COE的度数.
参考答案
答案为:C
答案为:C
答案为:C
答案为:B
答案为:D
答案为:B
答案为:B
答案为:C
答案为:A
答案为:D
答案为:北偏西60°
答案为:OB⊥OD
答案为:AB
C
l1
答案为:北偏西60°
答案为:BD
答案为:(1)CD (2)BC
解:如图所示.
解:DO⊥OE.理由:
因为OE平分∠COB,
所以∠COE=∠COB.
因为OD平分∠AOC,
所以∠DOC=∠AOC,
所以∠DOE=∠COE+∠DOC=∠COB+∠AOC=(∠COB+∠AOC)=∠AOB.
因为∠AOB是平角,
所以∠DOE=×180°=90°,
所以DO⊥OE.
解:∵OM⊥AB,NO⊥CD,
∴∠BOM=∠AOM=∠NOD=∠CON=90°.
(1)∵∠1=∠2,∴∠1=∠2=45°,
∴∠AOD=180°-∠2=180°-45°=135°,
即∠AOD的度数是135°.
(2)∵∠1+∠BOM=∠BOC,∠1=∠BOC,
∴∠1=∠BOM=30°,∴∠2=90°-∠1=60°.
∵∠1+∠MOD=∠COD=180°,
∴∠MOD=180°-∠1=150°.
90° 垂直的定义 50° 50° 等量代换 90°
OB OD 垂直的定义
(1)
∠AOE或∠COE
解:(1)因为OE是∠BOD的平分线,
所以∠DOE=∠BOE,
又因为∠BOE+∠AOE=180°,∠DOE+∠COE=180°,
所以∠DOE的补角是∠AOE或∠COE
(2)因为OE是∠BOD的平分线,∠BOD=62°,
所以∠BOE=∠BOD=31°,
所以∠AOE=180°-31°=149°,
因为∠BOD=62°,所以∠AOD=180°-62°=118°,
因为OF是∠AOD的平分线,
所以∠DOF=×118°=59°
(3)OE与OF的位置关系是OE⊥OF.理由如下:
因为OE,OF分别是∠BOD,∠AOD的平分线,
所以∠DOE=∠BOD,∠DOF=∠AOD,
因为∠BOD+∠AOD=180°,
所以∠EOF=∠DOE+∠DOF=(∠BOD+∠AOD)=90°,
所以OE⊥OF.
答案为:14°.
