24.1.2垂径定理的应用(共20张ppt)
文档属性
| 名称 | 24.1.2垂径定理的应用(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览





文档简介
24.1.2 垂径定理的应用
1、圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴.
∵直径CD垂直于弦AB,
·
O
A
B
C
D
E
∴AE=BE
AD=BD,AC=BC
⌒
⌒
⌒
⌒
2、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵直径CD平分弦AB,
·
O
A
B
C
D
E
∴CD⊥AB
AD=BD,AC=BC
⌒
⌒
⌒
⌒
3、推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
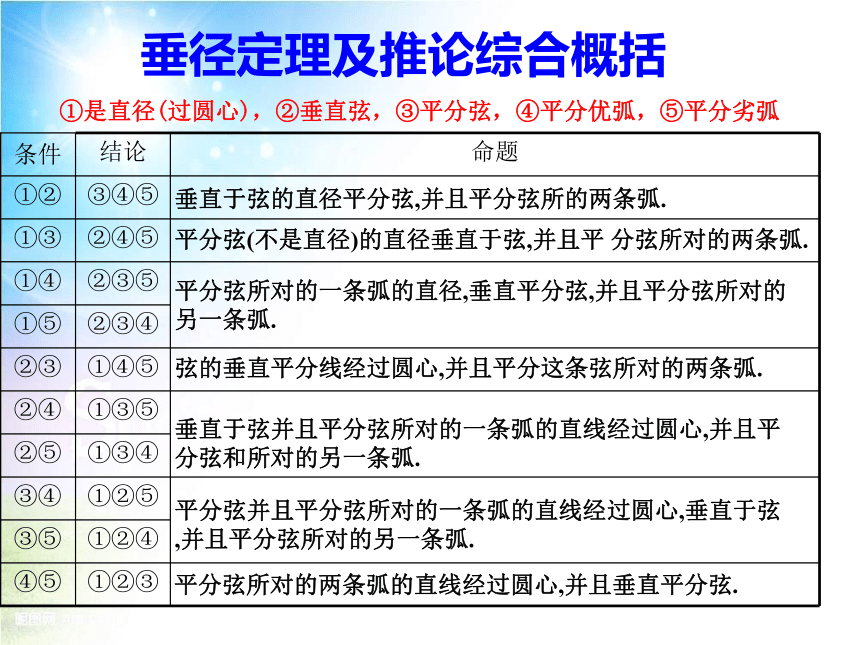
垂径定理及推论综合概括
条件
结论
命题
①②
③④⑤
①③
②④⑤
①④
②③⑤
①⑤
②③④
②③
①④⑤
②④
①③⑤
②⑤
①③④
③④
①②⑤
③⑤
①②④
④⑤
①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
①是直径(过圆心),②垂直弦,③平分弦,④平分优弧,⑤平分劣弧
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
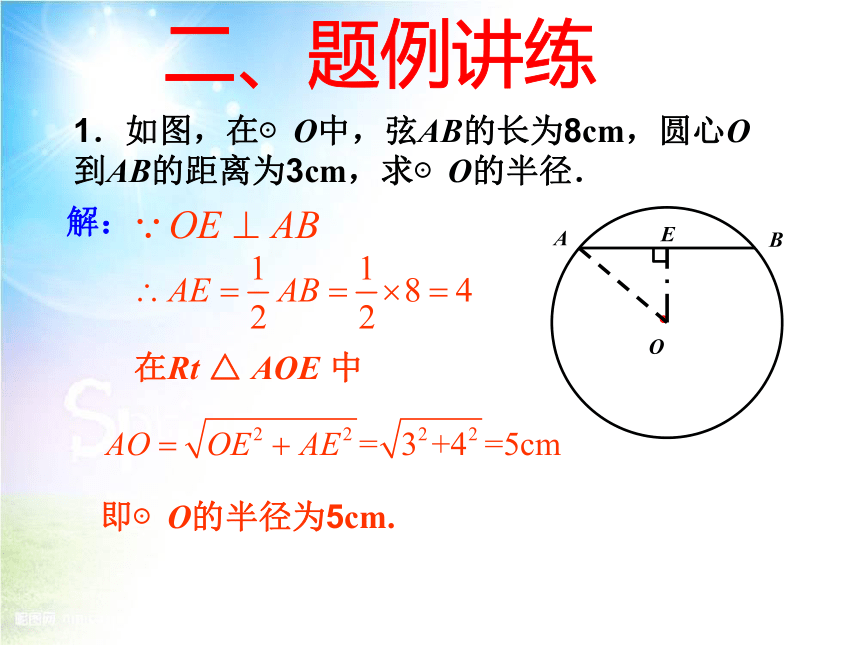
1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.
O
A
B
E
解:
即⊙O的半径为5cm.
在Rt △ AOE 中
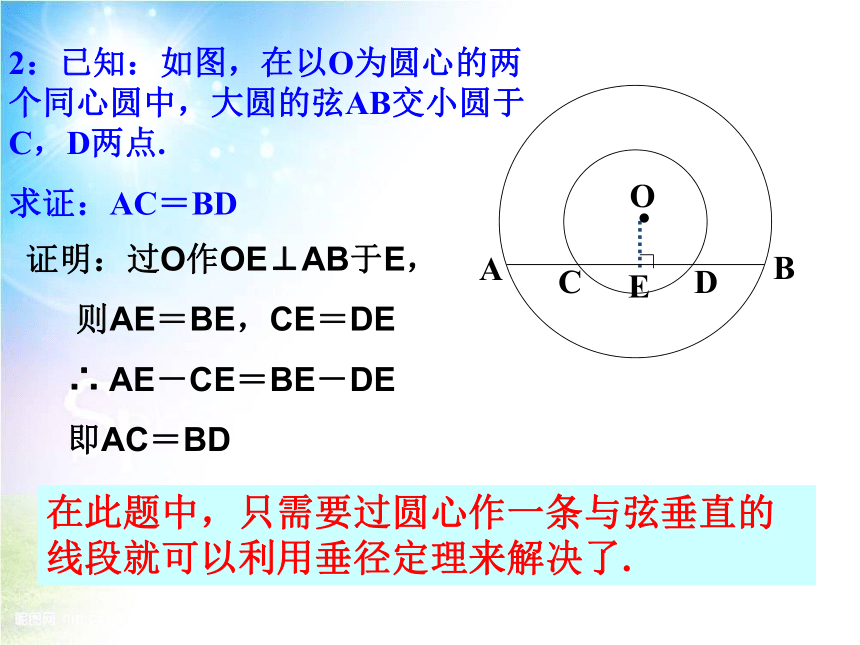
2:已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.
求证:AC=BD
证明:过O作OE⊥AB于E,
则AE=BE,CE=DE
∴ AE-CE=BE-DE
即AC=BD
E
.
A
C
D
B
O
在此题中,只需要过圆心作一条与弦垂直的线段就可以利用垂径定理来解决了.
3、已知:⊙O中弦AB∥CD。
求证:AC=BD
⌒
⌒
证明:作直径MN⊥AB。
∵AB∥CD,∴MN⊥CD。
则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弦)
AM-CM=BM-DM
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
M
C
D
A
B
O
N
你能讲解吗?
夹在平行弦间的两条弧相等.
你能有一句话概括一下吗?
小结:
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
1、如图,⊙O的直径为10,弦AB=8,P是弦AB上一个动点,则OP的取值范围是 .
O
A
B
P
3≤OP≤5
练习
2、如图,⊙O的直径AB和弦CD相交于点E,AE=1厘米,EB=5厘米,∠BED=30°,
求CD的长。
E
O
B
A
D
C
F
在Rt△OEF中,OE=3-1=2,
∠BED=30°则OF=1
又在Rt△DOF中
DF=
∴CD=2DF=
3、如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,
求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,且
又∵AC=AB ∴AE=AD
∴ 四边形ADOE为正方形.
(3)半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。
8cm
A
B
O
E
A
B
O
E
O
A
B
E
(1)半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 。
(2) ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 。
4、填空:
●O
A
B
C
D
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
(4)⊙O的半径为5cm,弦AB∥CD,
AB=8,CD=6,则AB、CD间的
距离是___ .
1cm
或7cm
解:如图,设半径为R,
在Rt⊿AOD中,由勾股定理,得
解得 R≈27.9(m).
答:赵州桥的主桥拱半径约为27.9m.
D
37.4
7.2
例:赵州桥主桥拱的跨度(弧所对的弦的长)为37.4m,
拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥
主桥拱的半径吗?(精确到0.1m)
AB =37.4,
CD =7.2
R
18.7
R-7.2
4、弓形的弦长为6cm,弓形的高
为2cm,则这弓形所在的圆的半径为 .
练习
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?
C
N
M
A
E
H
F
B
D
O
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
在Rt△OAD中,由勾股定理,得
解得 R=3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
1、在运用垂径定理来解决一些圆中线段的求解和证明时,常常要作垂直于弦的直径,而通常只需过圆心作弦的垂线段(弦心距)即可;
2、通过作出弦心距后,可构造直角三角形,然后用直角三角形的边角关系或勾股定理来求解.
1、圆是轴对称图形,经过圆心的每一条直线都是它们的对称轴.
∵直径CD垂直于弦AB,
·
O
A
B
C
D
E
∴AE=BE
AD=BD,AC=BC
⌒
⌒
⌒
⌒
2、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
∵直径CD平分弦AB,
·
O
A
B
C
D
E
∴CD⊥AB
AD=BD,AC=BC
⌒
⌒
⌒
⌒
3、推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
垂径定理及推论综合概括
条件
结论
命题
①②
③④⑤
①③
②④⑤
①④
②③⑤
①⑤
②③④
②③
①④⑤
②④
①③⑤
②⑤
①③④
③④
①②⑤
③⑤
①②④
④⑤
①②③
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
①是直径(过圆心),②垂直弦,③平分弦,④平分优弧,⑤平分劣弧
判断下列说法的正误
①平分弧的直径必平分弧所对的弦
②平分弦的直线必垂直弦
③垂直于弦的直径平分这条弦
④平分弦的直径垂直于这条弦
⑤弦的垂直平分线是圆的直径
⑥平分弦所对的一条弧的直径必垂直这条弦
⑦在圆中,如果一条直线经过圆心且平分弦,
必平分此弦所对的弧
1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.
O
A
B
E
解:
即⊙O的半径为5cm.
在Rt △ AOE 中
2:已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点.
求证:AC=BD
证明:过O作OE⊥AB于E,
则AE=BE,CE=DE
∴ AE-CE=BE-DE
即AC=BD
E
.
A
C
D
B
O
在此题中,只需要过圆心作一条与弦垂直的线段就可以利用垂径定理来解决了.
3、已知:⊙O中弦AB∥CD。
求证:AC=BD
⌒
⌒
证明:作直径MN⊥AB。
∵AB∥CD,∴MN⊥CD。
则AM=BM,CM=DM(垂直平分弦的直径平分弦所对的弦)
AM-CM=BM-DM
∴AC=BD
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
.
M
C
D
A
B
O
N
你能讲解吗?
夹在平行弦间的两条弧相等.
你能有一句话概括一下吗?
小结:
解决有关弦的问题,经常是过圆心作弦的垂线,或作垂直于弦的直径,连结半径等辅助线,为应用垂径定理创造条件。
.
C
D
A
B
O
M
N
E
.
A
C
D
B
O
.
A
B
O
1、如图,⊙O的直径为10,弦AB=8,P是弦AB上一个动点,则OP的取值范围是 .
O
A
B
P
3≤OP≤5
练习
2、如图,⊙O的直径AB和弦CD相交于点E,AE=1厘米,EB=5厘米,∠BED=30°,
求CD的长。
E
O
B
A
D
C
F
在Rt△OEF中,OE=3-1=2,
∠BED=30°则OF=1
又在Rt△DOF中
DF=
∴CD=2DF=
3、如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,
求证:四边形ADOE是正方形.
D
·
O
A
B
C
E
证明:
∴四边形ADOE为矩形,且
又∵AC=AB ∴AE=AD
∴ 四边形ADOE为正方形.
(3)半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。
8cm
A
B
O
E
A
B
O
E
O
A
B
E
(1)半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 。
(2) ⊙O的直径为10cm,圆心O到弦AB的 距离为3cm,则弦AB的长是 。
4、填空:
●O
A
B
C
D
1.两条弦在圆心的同侧
●O
A
B
C
D
2.两条弦在圆心的两侧
(4)⊙O的半径为5cm,弦AB∥CD,
AB=8,CD=6,则AB、CD间的
距离是___ .
1cm
或7cm
解:如图,设半径为R,
在Rt⊿AOD中,由勾股定理,得
解得 R≈27.9(m).
答:赵州桥的主桥拱半径约为27.9m.
D
37.4
7.2
例:赵州桥主桥拱的跨度(弧所对的弦的长)为37.4m,
拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥
主桥拱的半径吗?(精确到0.1m)
AB =37.4,
CD =7.2
R
18.7
R-7.2
4、弓形的弦长为6cm,弓形的高
为2cm,则这弓形所在的圆的半径为 .
练习
某地有一座圆弧形拱桥圆心为O,桥下水面宽度为7、2 m ,过O 作OC ⊥ AB 于D, 交圆弧于C,CD=2、4m, 现有一艘宽3m,船舱顶部为方形并高出水面(AB)2m的货船要经过拱桥,此货船能否顺利通过这座拱桥?
C
N
M
A
E
H
F
B
D
O
船能过拱桥吗
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设得
在Rt△OAD中,由勾股定理,得
解得 R=3.9(m).
在Rt△ONH中,由勾股定理,得
∴此货船能顺利通过这座拱桥.
1、在运用垂径定理来解决一些圆中线段的求解和证明时,常常要作垂直于弦的直径,而通常只需过圆心作弦的垂线段(弦心距)即可;
2、通过作出弦心距后,可构造直角三角形,然后用直角三角形的边角关系或勾股定理来求解.
同课章节目录
