24.1.4圆周角定理的应用(共14张ppt)
文档属性
| 名称 | 24.1.4圆周角定理的应用(共14张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 500.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览





文档简介
24.1.4 圆周角定理的应用
B
C
O
A
一条弧所对的圆周角等于它所对的圆心角的一半.
∠ACB= ∠AOB或∠AOB=2∠ACB
1、圆周角定义:
顶点在圆上,两边与圆相交的角叫做圆周角.
2、圆周角定理:
几何运用:
3、推论一:
同弧或等弧所对的圆周角相等
几何运用:
∠A=∠D(如图1)
或∵BC=EF ∴∠A=∠D(如图2)
在同圆或等圆中,相等的圆周角所对的弧相等
逆定理:
几何运用:
∵∠A=∠D ∴BC=EF(如图2)
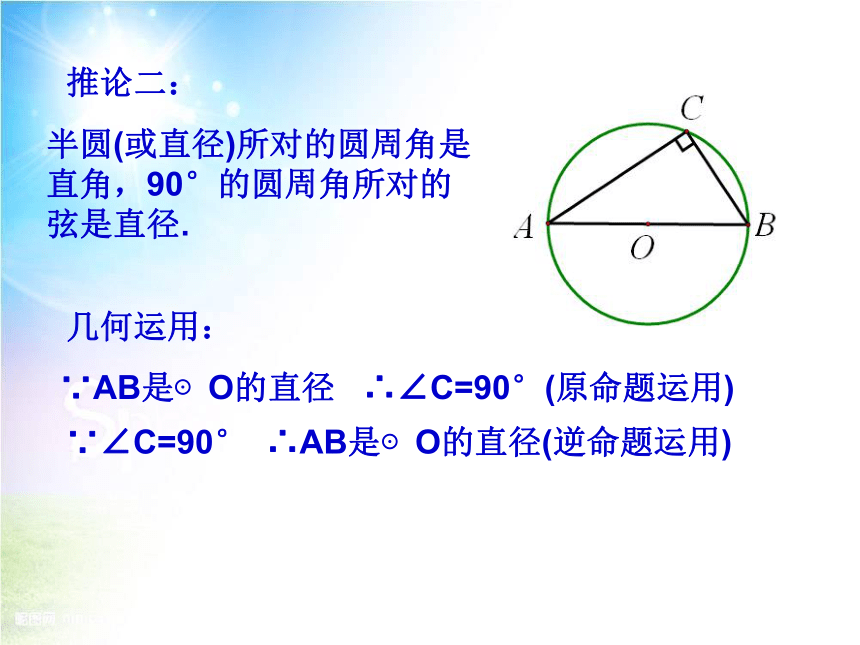
推论二:
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
几何运用:
∵AB是⊙O的直径 ∴∠C=90°(原命题运用)
∵∠C=90° ∴AB是⊙O的直径(逆命题运用)
二、问题探讨:
判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
P
不是
是
不是
不是
顶点不在圆上。
顶点在圆上,两边和圆相交。
两边不和圆相交。
有一边和圆不相交。
牛刀小试
1、如图,在⊙O中,∠ABC=50°
则∠AOC等于( )
A、50°; B、80°;
C、90°; D、100°
A
C
B
O
D
2、如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( )
A、30°; B、60°;
C、90°; D、45°
C
A
B
P
B
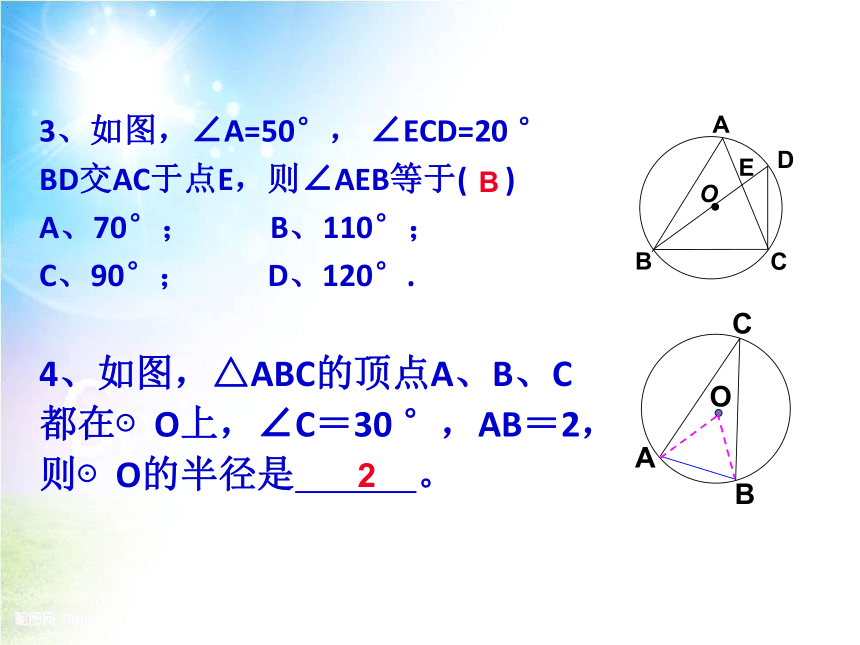
3、如图,∠A=50°, ∠ECD=20 °
BD交AC于点E,则∠AEB等于( )
A、70°; B、110°;
C、90°; D、120°.
B
4、如图,△ABC的顶点A、B、C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 。
A
C
B
O
D
E
C
A
B
O
2
例1、 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
在等腰Rt△ABD中,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD ∴AD=BD
例题评析
例2、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点
C,使DC=BD,连接AC交⊙O于点F,点F不与点A重合.
(1)AB与AC的大小有什么关系?为什么?
(2)若AF=6,AB=10,求BC的长.
A
C
B
D
F
O
解:(1) AB=AC
证明:连接AD
又∵DC=BD,∴AB=AC
∵AB是直径,∴∠ADB=90°
(2)连接BF
∵AB是直径 ∴∠AFB=90°
又∵AF=6 AB=10
在Rt△BCF中,∵CF=AC-AF=10-6=4
1.如图,点A、B、C在⊙O上,AO∥BC,∠OAC=20°则∠OBC的度数是( )
A、10° B、20°
C、40° D、70°
C
O
A
B
C
2.如图,△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为( )
A、 B、4
C、 D、 5
O
B
A
C
A
3.如图,点A、B、C是上的三点,∠ACB=26°则∠BAO的度数是________。
O
C
B
A
4.如图,点A、B、C是⊙O上的三点,且∠AOC=80°则∠ABC的度数为 。
64°
140°
5.如图,⊙O的直径CD过弦EF的中点G ,∠EOD=40°则∠DCF等于________。
E
F
C
D
O
G
20°
α
6、已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:BD=DE
证明:连接AD.
∵AB是圆的直径,
∴∠ADB=90°
即AD⊥BC
∵AB=AC,
∴∠BAD=∠CAD,
⌒ ⌒
∴BD= DE
A
B
C
D
E
拓展练习
在教材P87页例4的条件下如何求CD的长?
E
由原题解答的结论可知:AD=
过点A作AE⊥CD于E,在Rt△ACE中
∵∠ACE= ∠ACB=45°
∴CE=AE= AC=
在Rt△ADE中,由勾股定理得:
∴
∴CD=CE+DE=
作业:
1、教材P89T第5题、
2、教材P90T第14题.
B
C
O
A
一条弧所对的圆周角等于它所对的圆心角的一半.
∠ACB= ∠AOB或∠AOB=2∠ACB
1、圆周角定义:
顶点在圆上,两边与圆相交的角叫做圆周角.
2、圆周角定理:
几何运用:
3、推论一:
同弧或等弧所对的圆周角相等
几何运用:
∠A=∠D(如图1)
或∵BC=EF ∴∠A=∠D(如图2)
在同圆或等圆中,相等的圆周角所对的弧相等
逆定理:
几何运用:
∵∠A=∠D ∴BC=EF(如图2)
推论二:
半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
几何运用:
∵AB是⊙O的直径 ∴∠C=90°(原命题运用)
∵∠C=90° ∴AB是⊙O的直径(逆命题运用)
二、问题探讨:
判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
P
不是
是
不是
不是
顶点不在圆上。
顶点在圆上,两边和圆相交。
两边不和圆相交。
有一边和圆不相交。
牛刀小试
1、如图,在⊙O中,∠ABC=50°
则∠AOC等于( )
A、50°; B、80°;
C、90°; D、100°
A
C
B
O
D
2、如图,△ABC是等边三角形,
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( )
A、30°; B、60°;
C、90°; D、45°
C
A
B
P
B
3、如图,∠A=50°, ∠ECD=20 °
BD交AC于点E,则∠AEB等于( )
A、70°; B、110°;
C、90°; D、120°.
B
4、如图,△ABC的顶点A、B、C
都在⊙O上,∠C=30 °,AB=2,
则⊙O的半径是 。
A
C
B
O
D
E
C
A
B
O
2
例1、 如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.
在等腰Rt△ABD中,
解:∵AB是直径,
∴ ∠ACB= ∠ADB=90°.
在Rt△ABC中,
∵CD平分∠ACB,
∴AD=BD ∴AD=BD
例题评析
例2、如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点
C,使DC=BD,连接AC交⊙O于点F,点F不与点A重合.
(1)AB与AC的大小有什么关系?为什么?
(2)若AF=6,AB=10,求BC的长.
A
C
B
D
F
O
解:(1) AB=AC
证明:连接AD
又∵DC=BD,∴AB=AC
∵AB是直径,∴∠ADB=90°
(2)连接BF
∵AB是直径 ∴∠AFB=90°
又∵AF=6 AB=10
在Rt△BCF中,∵CF=AC-AF=10-6=4
1.如图,点A、B、C在⊙O上,AO∥BC,∠OAC=20°则∠OBC的度数是( )
A、10° B、20°
C、40° D、70°
C
O
A
B
C
2.如图,△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为( )
A、 B、4
C、 D、 5
O
B
A
C
A
3.如图,点A、B、C是上的三点,∠ACB=26°则∠BAO的度数是________。
O
C
B
A
4.如图,点A、B、C是⊙O上的三点,且∠AOC=80°则∠ABC的度数为 。
64°
140°
5.如图,⊙O的直径CD过弦EF的中点G ,∠EOD=40°则∠DCF等于________。
E
F
C
D
O
G
20°
α
6、已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
求证:BD=DE
证明:连接AD.
∵AB是圆的直径,
∴∠ADB=90°
即AD⊥BC
∵AB=AC,
∴∠BAD=∠CAD,
⌒ ⌒
∴BD= DE
A
B
C
D
E
拓展练习
在教材P87页例4的条件下如何求CD的长?
E
由原题解答的结论可知:AD=
过点A作AE⊥CD于E,在Rt△ACE中
∵∠ACE= ∠ACB=45°
∴CE=AE= AC=
在Rt△ADE中,由勾股定理得:
∴
∴CD=CE+DE=
作业:
1、教材P89T第5题、
2、教材P90T第14题.
同课章节目录
