人教版数学九年级下册 27.3 《位似》同步测试 (Word版 含答案)
文档属性
| 名称 | 人教版数学九年级下册 27.3 《位似》同步测试 (Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 675.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览



文档简介
人教版数学九下《位似》同步测试
一、选择题
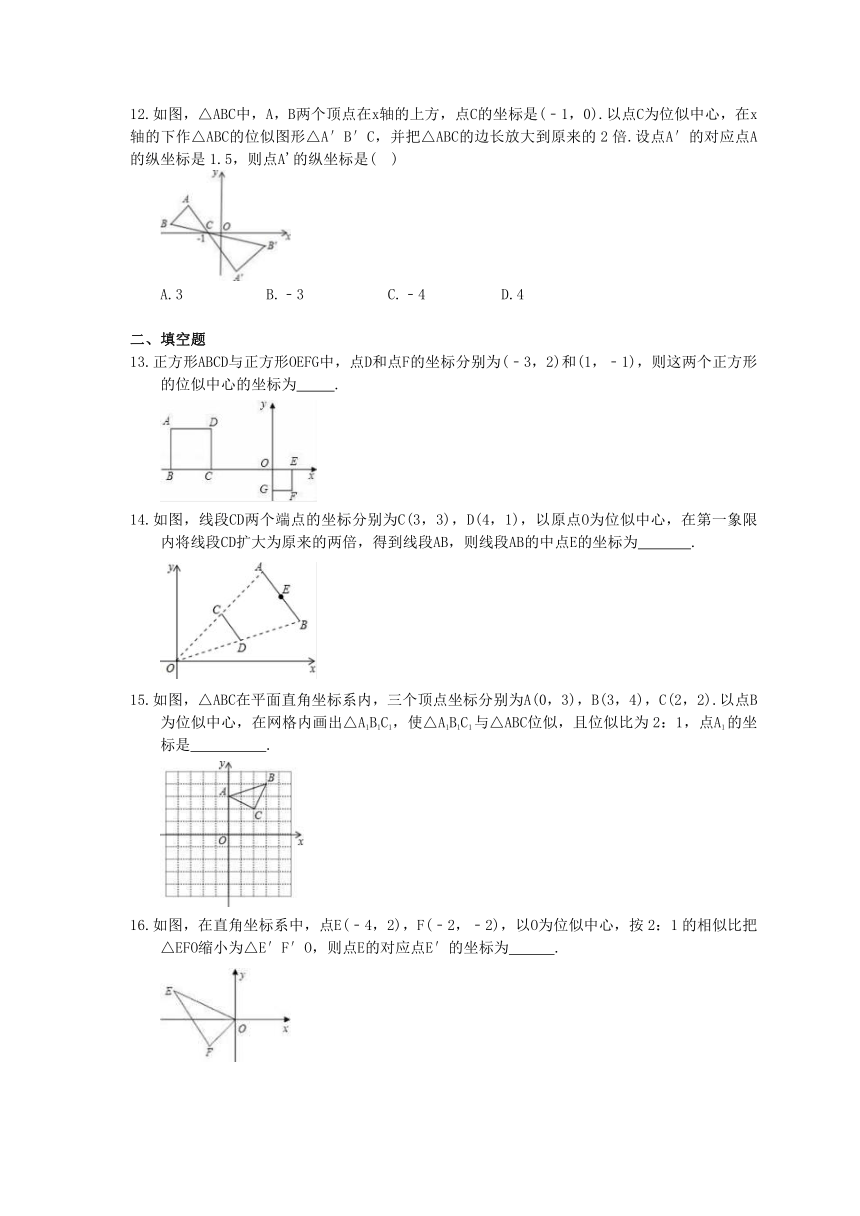
1.如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(
)
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
2.已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),
以点B为位似中心,且位似比为1:2将△ABC放大得△A1BC1
,则点C1
的坐标为(
)
A.(1,0)
B.(5,8)
C.(4,6)或(5,8)
D.(1,0)或(5,8)
3.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为(
)
A.P1
B.P2
C.P3
D.P4
4.如图.位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投影三角形的对应边长为(
)
A.8cm
B.20cm
C.3.2cm
D.10cm
5.“标准对数视力表”对我们来说并不陌生,图3是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形(
)
A.左上
B.左下
C.右上
D.右下
6.如图是小孔成像原理示意图,根据图中尺寸,蜡烛在暗盒中所成的像CD的长是(
)
A.cm
B.cm
C.
cm
D.1cm
7.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是(
)
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
8.如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B的对应点B′的坐标是(
)
A.(﹣3,﹣1)
B.(﹣1,2)
C.(﹣9,1)或(9,﹣1)
D.(﹣3,﹣1)或(3,1)
9.下列说法正确的是(
)
A.位似图形可以通过平移得到
B.相似图形一定是位似图形,位似图形一定是相似图形
C.位似图形的位似中心不只有一个
D.位似中心到对应点的距离之比都相等
10.如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为(
)
A.(﹣a,﹣2b)
B.(﹣2a,﹣b)
C.(﹣2a,﹣2b)
D.(﹣b,﹣2a)
11.图中的两个四边形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
12.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是(
)
A.3
B.﹣3
C.﹣4
D.4
二、填空题
13.正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为
.
14.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为
.
15.如图,△ABC在平面直角坐标系内,三个顶点坐标分别为A(0,3),B(3,4),C(2,2).以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点A1的坐标是
.
16.如图,在直角坐标系中,点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按2:1的相似比把△EFO缩小为△E′F′O,则点E的对应点E′的坐标为
.
17.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是
.
18.如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是
.
三、作图题
19.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是
.
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,
△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)在图1中画出△ABC关于x轴对称的△A1B1C1;
(2)在图1中画出将△ABC绕原点O按逆时针方向旋转90°所得的△A2B2C2;
(3)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A3B3C3与△ABC的对应边
的比为2:1(画出一种即可).直接写出点A的对应点A3的坐标.
21.小金鱼在直角坐标系中的位置如图所示,根据图形解答下面的问题:
(1)分别写出小金鱼身上点A、B、C、D、E、F的坐标;
(2)小金鱼身上的点的纵坐标都乘以﹣1,横坐标不变.作出相应图形,它与原图案有怎样的位置关系?
22.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
23.已知,△DEF是△ABC的位似三角形(点D、E、F分别对应点A、B、C),原点O为位似中心,△DEF与△ABC的位似比为k.
(1)若位似比k=,请你在平面直角坐标系的第四象限中画出△DEF;
(2)若位似比k=m,△ABC的周长为C,则△DEF的周长=
;
(3)若位似比k=n,△ABC的面积为S,则△DEF的面积=
.
24.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;(3)四边形AA2C2C的面积是
平方单位.
参考答案
答案为:C;.
答案为:D;
答案为:B;
答案为:B;.
答案为:B;
答案为:D;
答案为:A;
答案为:D;
答案为:D;
答案为:C;
答案为:D;
答案为:B;.
答案为:(﹣1,0)或(5,﹣2).
答案为:(7,4).
答案为:(﹣3,2).
答案为:(2,﹣1)或(﹣2,1).
答案为:(4,2)或(﹣4,﹣2).
答案为:(﹣2,).
解:(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,
点C1的坐标是(2,﹣2);
(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,
且位似比为2:1,点C2的坐标是(1,0),
故答案为:(1)(2,﹣2);(2)(1,0)
解:(1)如图1,△A1B1C1为所作;
(2)如图1,△A2B2C2为所作;
(3)如图2,△A3B3C3△ABC为所作,此时点A的对应点A3的坐标是(﹣4,﹣4).
解:(1)如图所示:A(0,﹣4),B(4,0),C(4,﹣7),D(10,﹣3),
E(10,﹣5),F(8,﹣4);
(2)如图所示:它与原图案关于x轴对称.
如图所示:
解:(1)如图所示,
则△DEF为所求的三角形;
(2)∵位似比k=m,△ABC的周长为C,∴△DEF的周长=mC;
(3)∵位似比k=n,△ABC的面积为S,∴△DEF的面积=n2S.
解:(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,
点C1的坐标是(2,﹣2);
(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,
且位似比为2:1,
(3)四边形AA2C2C的面积是=;
故答案为:(1)(2,﹣2);(2)7.5
一、选择题
1.如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(
)
A.(0,3)
B.(0,2.5)
C.(0,2)
D.(0,1.5)
2.已知△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2),
以点B为位似中心,且位似比为1:2将△ABC放大得△A1BC1
,则点C1
的坐标为(
)
A.(1,0)
B.(5,8)
C.(4,6)或(5,8)
D.(1,0)或(5,8)
3.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为(
)
A.P1
B.P2
C.P3
D.P4
4.如图.位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投影三角形的对应边长为(
)
A.8cm
B.20cm
C.3.2cm
D.10cm
5.“标准对数视力表”对我们来说并不陌生,图3是视力表的一部分,其中最上面较大的“E”与下面四个较小“E”中的哪一个是位似图形(
)
A.左上
B.左下
C.右上
D.右下
6.如图是小孔成像原理示意图,根据图中尺寸,蜡烛在暗盒中所成的像CD的长是(
)
A.cm
B.cm
C.
cm
D.1cm
7.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是(
)
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
8.如图,在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B的对应点B′的坐标是(
)
A.(﹣3,﹣1)
B.(﹣1,2)
C.(﹣9,1)或(9,﹣1)
D.(﹣3,﹣1)或(3,1)
9.下列说法正确的是(
)
A.位似图形可以通过平移得到
B.相似图形一定是位似图形,位似图形一定是相似图形
C.位似图形的位似中心不只有一个
D.位似中心到对应点的距离之比都相等
10.如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为(
)
A.(﹣a,﹣2b)
B.(﹣2a,﹣b)
C.(﹣2a,﹣2b)
D.(﹣b,﹣2a)
11.图中的两个四边形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
12.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(﹣1,0).以点C为位似中心,在x轴的下作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点A′的对应点A的纵坐标是1.5,则点A'的纵坐标是(
)
A.3
B.﹣3
C.﹣4
D.4
二、填空题
13.正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为
.
14.如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为
.
15.如图,△ABC在平面直角坐标系内,三个顶点坐标分别为A(0,3),B(3,4),C(2,2).以点B为位似中心,在网格内画出△A1B1C1,使△A1B1C1与△ABC位似,且位似比为2:1,点A1的坐标是
.
16.如图,在直角坐标系中,点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按2:1的相似比把△EFO缩小为△E′F′O,则点E的对应点E′的坐标为
.
17.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABC的三个顶点均在格点(网格线的交点)上.以原点O为位似中心,画△A1B1C1,使它与△ABC的相似比为2,则点B的对应点B1的坐标是
.
18.如图,在直角坐标系中,每个小方格的边长均为1,△AOB与△A′OB′是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是
.
三、作图题
19.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是
.
20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,
△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)在图1中画出△ABC关于x轴对称的△A1B1C1;
(2)在图1中画出将△ABC绕原点O按逆时针方向旋转90°所得的△A2B2C2;
(3)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A3B3C3与△ABC的对应边
的比为2:1(画出一种即可).直接写出点A的对应点A3的坐标.
21.小金鱼在直角坐标系中的位置如图所示,根据图形解答下面的问题:
(1)分别写出小金鱼身上点A、B、C、D、E、F的坐标;
(2)小金鱼身上的点的纵坐标都乘以﹣1,横坐标不变.作出相应图形,它与原图案有怎样的位置关系?
22.如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
23.已知,△DEF是△ABC的位似三角形(点D、E、F分别对应点A、B、C),原点O为位似中心,△DEF与△ABC的位似比为k.
(1)若位似比k=,请你在平面直角坐标系的第四象限中画出△DEF;
(2)若位似比k=m,△ABC的周长为C,则△DEF的周长=
;
(3)若位似比k=n,△ABC的面积为S,则△DEF的面积=
.
24.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是
;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;(3)四边形AA2C2C的面积是
平方单位.
参考答案
答案为:C;.
答案为:D;
答案为:B;
答案为:B;.
答案为:B;
答案为:D;
答案为:A;
答案为:D;
答案为:D;
答案为:C;
答案为:D;
答案为:B;.
答案为:(﹣1,0)或(5,﹣2).
答案为:(7,4).
答案为:(﹣3,2).
答案为:(2,﹣1)或(﹣2,1).
答案为:(4,2)或(﹣4,﹣2).
答案为:(﹣2,).
解:(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,
点C1的坐标是(2,﹣2);
(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,
且位似比为2:1,点C2的坐标是(1,0),
故答案为:(1)(2,﹣2);(2)(1,0)
解:(1)如图1,△A1B1C1为所作;
(2)如图1,△A2B2C2为所作;
(3)如图2,△A3B3C3△ABC为所作,此时点A的对应点A3的坐标是(﹣4,﹣4).
解:(1)如图所示:A(0,﹣4),B(4,0),C(4,﹣7),D(10,﹣3),
E(10,﹣5),F(8,﹣4);
(2)如图所示:它与原图案关于x轴对称.
如图所示:
解:(1)如图所示,
则△DEF为所求的三角形;
(2)∵位似比k=m,△ABC的周长为C,∴△DEF的周长=mC;
(3)∵位似比k=n,△ABC的面积为S,∴△DEF的面积=n2S.
解:(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,
点C1的坐标是(2,﹣2);
(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,
且位似比为2:1,
(3)四边形AA2C2C的面积是=;
故答案为:(1)(2,﹣2);(2)7.5
