沪教版(上海)初中数学七年级第一学期 10.5 可化为一元一次方程的分式方程 (1)学案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 10.5 可化为一元一次方程的分式方程 (1)学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 101.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 18:22:52 | ||
图片预览



文档简介
七年级第一学期学习任务单
《10.5
可化为一元一次方程的分式方程(1)》
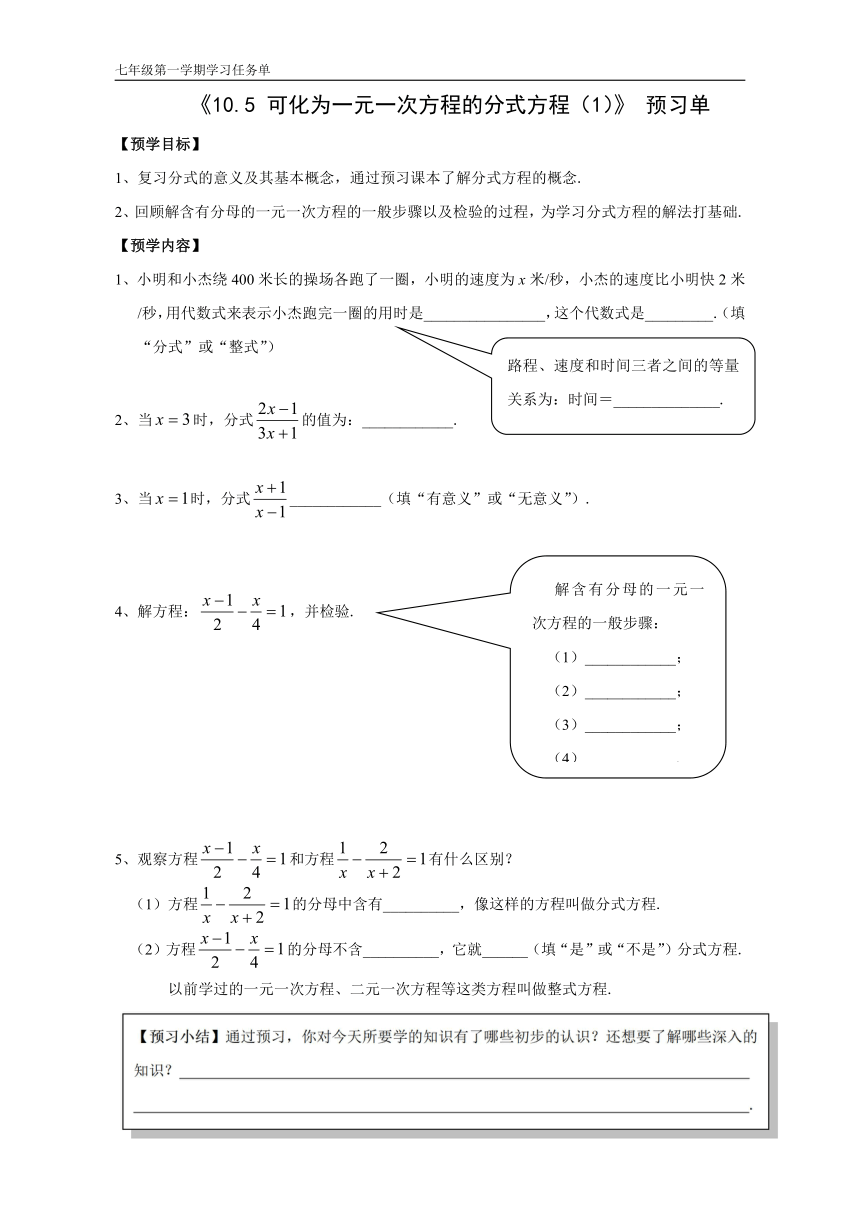
预习单
【预学目标】
1、复习分式的意义及其基本概念,通过预习课本了解分式方程的概念.
2、回顾解含有分母的一元一次方程的一般步骤以及检验的过程,为学习分式方程的解法打基础.
【预学内容】
1、小明和小杰绕400米长的操场各跑了一圈,小明的速度为x米/秒,小杰的速度比小明快2米/秒,用代数式来表示小杰跑完一圈的用时是________________,这个代数式是_________.(填“分式”或“整式”)
2、当时,分式的值为:____________.
3、当时,分式____________(填“有意义”或“无意义”).
4、解方程:,并检验.
5、观察方程和方程有什么区别?
(1)方程的分母中含有__________,像这样的方程叫做分式方程.
(2)方程的分母不含__________,它就______(填“是”或“不是”)分式方程.
以前学过的一元一次方程、二元一次方程等这类方程叫做整式方程.
《10.5
可化为一元一次方程的分式方程(1)》
学习任务单
【学习目标】
1、理解分式方程及可化为一元一次方程的分式方程的意义.
2、熟练解可化为一元一次方程的分式方程,知道分式方程需检验,初步了解增根产生的原因.
3、通过学习分式方程的解法,领悟将分式方程转化为整式方程的化归思想.
【学习重点和难点】
理解分式方程及可化为一元一次方程的分式方程的意义;能够熟练解可化为一元一次方程的分式方程;知道分式方程需检验,初步了解增根产生的原因.
【探究新知】
预习检测:下列方程中,哪些是分式方程?
(1);
(2);
(3);
(4).
活动1:小明和小杰在400米的跑道上分别练习竞走和长跑,已知小杰的跑步速度是小明竞走速度的2倍,结果两人各自完成一圈时,小明比小杰多用了80秒,求两人的速度分别是多少?
(1)根据题意,设未知数,列方程.
设________________________________,则_______________________________
得_________________________________________________.
(2)如何解(1)中得到的方程呢?请同学们小组讨论如何解这个分式方程.
小结:解分式方程,需要在方程两边同时______________(即去分母),从而将分式方程转化为________方程.
活动2:(1)实践:解分式方程并检验.
(2)讨论:将分式方程转化为整式方程后解得的根是否一定是原分式方程的根?
增根的含义:将分式方程转化为________,如果整式方程的根使分式方程的_____________
______,那么这样的根就叫做分式方程的增根.
(3)思考:解分式方程需不需要检验?如果需要,如何检验比较方便?
【巩固新知】
例题1:解分式方程.
例题2:小明的学习小组中有两位同学解了两个分式方程,我们来看看做的是否正确,如果不正确,请你帮忙指正.
(1)将方程去分母,得,解得,所以,原方程无解.
(
)
改正:______________________________________________________________.
(2)将方程去分母,得,解得,所以,原方程的解为.
(
)
改正:______________________________________________________________.
【能力提升】
例题3:已知关于x的方程有增根,求k的值.
自主学习评价(请填写“好”、“较好”、“一般”或“需努力”)
参与讨论与发言
组员互助
对本节课知识点的掌握程度
自评
组员互评
【课内检测】
1、下列方程中,_______________________是分式方程(在横线上填上序号).
①
;
②
;
③
;
④
.
2、下列分式方程的根是x=2的是………………………………………………………(
)
(A);
(B);
(C);
(D).
3、若关于x的方程有增根,则这个增根是____________,k的值为_________.
4、解下列方程:
(1);
(2);
(3);
(4).
5、小丽、小明练习打字,小丽比小明每分钟多打35个字,小丽打400个字的时间与小明打300个字的时间相同,问小丽、小明每分钟分别可打多少字?
《10.5
可化为一元一次方程的分式方程(1)》课后检测
班级________
姓名_________
完成时间_________
家长签字_________
一、填空和选择:
1.
叫做分式方程,
叫做整式方程.
2.解分式方程的关键是
,将其转化为已学过的
再求解.
3.解分式方程必须要
,方法有两种:
一是代入
检验.二是代入
检验.
4.下列方程的根为的是………………………………………………………………(
)
;
;
;
.
5.下列方程哪些是整式方程,哪些是分式方程?(在横线上填写方程的编号)
①;
②;
③;
④;
⑤3x-1=2;⑥
其中整式方程是_____________________,分式方程是_____________________.
6.请你写出一个可以化为一元一次方程的分式方程:________________.
7.方程的解是________________.
8.方程的解是________________.
9.方程的解是________________.
10.分式方程________________(填“有解”或“无解”).
11.如果关于的方程有增根,那么这个增根是___________,__________.
二、简答题:
12.解下列方程:
(1);
(2);
(3);
(4);
(5);
(6).
13.当m为何值时,关于x的方程无解?
14.一个分数,分母和分子之和为8,若分子增加3,则新分数值是原分数值的2倍,求原分数.
三、预习新知:请你预习书本P84~85相关分式方程的应用问题,并完成下列预习检测
15.现有一辆火车从上海出发开往南京,又从南京返回上海,已知上海和南京两地相距390千米,火车返回时的速度比去时的速度增加了50%,火车一来一回共用了6.5小时,求火车往返的速度各多少?
《10.5
可化为一元一次方程的分式方程(1)》
预习单
【预学目标】
1、复习分式的意义及其基本概念,通过预习课本了解分式方程的概念.
2、回顾解含有分母的一元一次方程的一般步骤以及检验的过程,为学习分式方程的解法打基础.
【预学内容】
1、小明和小杰绕400米长的操场各跑了一圈,小明的速度为x米/秒,小杰的速度比小明快2米/秒,用代数式来表示小杰跑完一圈的用时是________________,这个代数式是_________.(填“分式”或“整式”)
2、当时,分式的值为:____________.
3、当时,分式____________(填“有意义”或“无意义”).
4、解方程:,并检验.
5、观察方程和方程有什么区别?
(1)方程的分母中含有__________,像这样的方程叫做分式方程.
(2)方程的分母不含__________,它就______(填“是”或“不是”)分式方程.
以前学过的一元一次方程、二元一次方程等这类方程叫做整式方程.
《10.5
可化为一元一次方程的分式方程(1)》
学习任务单
【学习目标】
1、理解分式方程及可化为一元一次方程的分式方程的意义.
2、熟练解可化为一元一次方程的分式方程,知道分式方程需检验,初步了解增根产生的原因.
3、通过学习分式方程的解法,领悟将分式方程转化为整式方程的化归思想.
【学习重点和难点】
理解分式方程及可化为一元一次方程的分式方程的意义;能够熟练解可化为一元一次方程的分式方程;知道分式方程需检验,初步了解增根产生的原因.
【探究新知】
预习检测:下列方程中,哪些是分式方程?
(1);
(2);
(3);
(4).
活动1:小明和小杰在400米的跑道上分别练习竞走和长跑,已知小杰的跑步速度是小明竞走速度的2倍,结果两人各自完成一圈时,小明比小杰多用了80秒,求两人的速度分别是多少?
(1)根据题意,设未知数,列方程.
设________________________________,则_______________________________
得_________________________________________________.
(2)如何解(1)中得到的方程呢?请同学们小组讨论如何解这个分式方程.
小结:解分式方程,需要在方程两边同时______________(即去分母),从而将分式方程转化为________方程.
活动2:(1)实践:解分式方程并检验.
(2)讨论:将分式方程转化为整式方程后解得的根是否一定是原分式方程的根?
增根的含义:将分式方程转化为________,如果整式方程的根使分式方程的_____________
______,那么这样的根就叫做分式方程的增根.
(3)思考:解分式方程需不需要检验?如果需要,如何检验比较方便?
【巩固新知】
例题1:解分式方程.
例题2:小明的学习小组中有两位同学解了两个分式方程,我们来看看做的是否正确,如果不正确,请你帮忙指正.
(1)将方程去分母,得,解得,所以,原方程无解.
(
)
改正:______________________________________________________________.
(2)将方程去分母,得,解得,所以,原方程的解为.
(
)
改正:______________________________________________________________.
【能力提升】
例题3:已知关于x的方程有增根,求k的值.
自主学习评价(请填写“好”、“较好”、“一般”或“需努力”)
参与讨论与发言
组员互助
对本节课知识点的掌握程度
自评
组员互评
【课内检测】
1、下列方程中,_______________________是分式方程(在横线上填上序号).
①
;
②
;
③
;
④
.
2、下列分式方程的根是x=2的是………………………………………………………(
)
(A);
(B);
(C);
(D).
3、若关于x的方程有增根,则这个增根是____________,k的值为_________.
4、解下列方程:
(1);
(2);
(3);
(4).
5、小丽、小明练习打字,小丽比小明每分钟多打35个字,小丽打400个字的时间与小明打300个字的时间相同,问小丽、小明每分钟分别可打多少字?
《10.5
可化为一元一次方程的分式方程(1)》课后检测
班级________
姓名_________
完成时间_________
家长签字_________
一、填空和选择:
1.
叫做分式方程,
叫做整式方程.
2.解分式方程的关键是
,将其转化为已学过的
再求解.
3.解分式方程必须要
,方法有两种:
一是代入
检验.二是代入
检验.
4.下列方程的根为的是………………………………………………………………(
)
;
;
;
.
5.下列方程哪些是整式方程,哪些是分式方程?(在横线上填写方程的编号)
①;
②;
③;
④;
⑤3x-1=2;⑥
其中整式方程是_____________________,分式方程是_____________________.
6.请你写出一个可以化为一元一次方程的分式方程:________________.
7.方程的解是________________.
8.方程的解是________________.
9.方程的解是________________.
10.分式方程________________(填“有解”或“无解”).
11.如果关于的方程有增根,那么这个增根是___________,__________.
二、简答题:
12.解下列方程:
(1);
(2);
(3);
(4);
(5);
(6).
13.当m为何值时,关于x的方程无解?
14.一个分数,分母和分子之和为8,若分子增加3,则新分数值是原分数值的2倍,求原分数.
三、预习新知:请你预习书本P84~85相关分式方程的应用问题,并完成下列预习检测
15.现有一辆火车从上海出发开往南京,又从南京返回上海,已知上海和南京两地相距390千米,火车返回时的速度比去时的速度增加了50%,火车一来一回共用了6.5小时,求火车往返的速度各多少?
