15.3分式方程(1) 课件(共19张PPT)
文档属性
| 名称 | 15.3分式方程(1) 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 08:49:43 | ||
图片预览






文档简介
(共19张PPT)
人教版
八年级数学上
15.3分式方程
---第一课时
教学目标
1.掌握解分式方程的基本思路和解法.(重点)
2.理解分式方程时可能无解的原因.(难点)
合作探究---分式方程的概念
一艘轮船在静水中的最大航速为30
km/h,它沿江以最大航速顺流航行90
km所用时间,与以最大航速逆流航行60
km所用时间相等,江水的流速为多少?
题目中相等的数量关系是:
解:设江水的流速为v
km/h.
依题意得:
仔细观察这个方程,未知数的位置有什么特点?
分式的定义:分母中含未知数的方程叫做分式方程.
合作探究---分式方程的概念
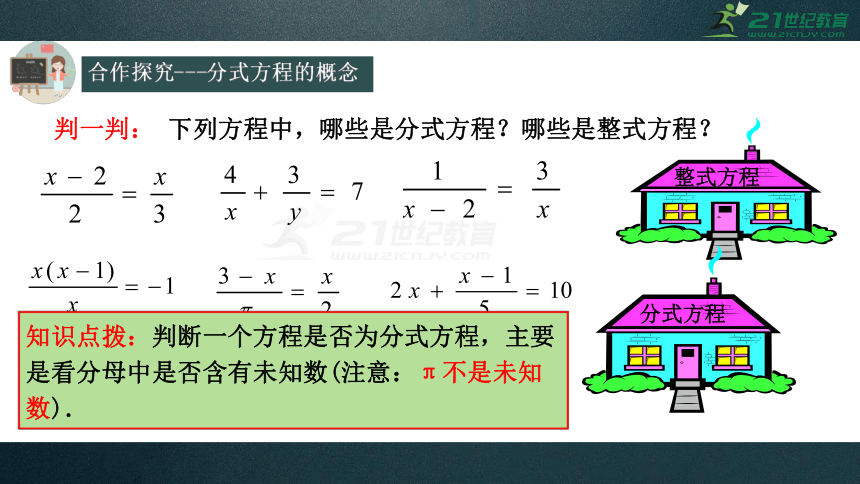
判一判:
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
知识点拨:判断一个方程是否为分式方程,主要是看分母中是否含有未知数(注意:π不是未知数).
合作探究---分式方程的解法
问题1:你能试着解这个分式方程吗?
思考2:如何去分母?
思考3:在方程两边乘什么样的式子才能把每一个分母都约去?
思考4:这样做的依据是什么?
思考1:能否将它转化为整式方程呢?
合作探究---分式方程的解法
解:方程①两边同乘(30+x)(30-x),得:
检验:将x=6代入原分式方程中,
左边=
=右边,
因此x=6是原分式方程的解.
90(30-x)=60(30+x),
解得:
x=6.
x=6是原分式方程的解吗?
答:江水的流速为6km/h.
知识点拨:解分式方程的基本思路:是将分式方程化为整式方程,具体做法是“去分母”
即方程两边同乘最简公分母.这也是解分式方程的一般方法.
针对训练
解:方程两边乘最简公分母
(x+5)(x-5)得,
解得,x=5
x+5=10
检验:把x
=
5
代入原方程中,发现x-5和x2-25的值都为0,相应的分式无意义,因此x=5虽是方程x+5=10的解,但不是原分式方程
的解.实际上,这个分式方程无解.
解分式方程:
合作探究
问题2
:上面两个分式方程中,为什么
去分母后得到的整式方程的解就是它的解,而
去分母后得到的整式方程的解,却不是原分式方程的解呢?
合作探究
我们来观察去分母的过程:
解:方程两边都乘
(30+v)(30-v)得,
解得,v=6
90(30-v)=60(30+v)
解:方程两边都乘
(x+5)(x-5)得,
解得,
x=5
x+5=10
当v=6时,
(30+v)(30-v)≠0
当x=5时,
(x+5)(x-5)=0
整式方程的解与分式方程的解相同
整式方程的解不是分式方程的解
真相揭秘:
第一个分式方程两边同乘了不为0的式子,所得整式方程的解与分式方程的解相同.
真相揭秘:
第二个分式方程两边同乘了等于0的式子,所得整式方程的解与分式方程的解不相同.
合作探究
解分式方程时,去分母后所得整式方程的解有可能使原方程的分母为0,所以分式方程的解必须检验.
怎样检验?
这个整式方程的解是不是原分式的解呢?
分式方程解的检验------必不可少的步骤!
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
典例精析
例1:解方程
解:(1)方程两边乘
x(x-3)得,
解得,
2x=3x-9
x=9
检验:当x=9时,
x(x-3)≠0.
所以,原分式方程的解为x=9.
(2)方程两边同乘以
(x-1)
(x+2)
,
得
x(x+2)-(x-1)(x+2)=3
解得
,
检验:当x
=
1
时,(x-1)
(x+2)=0,因此x
=1不是原分式方程的解.
x
=
1
所以,原分式方程无解.
归纳总结
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
x=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分母为0
小试牛刀
D
2.
要把方程
化为整式方程,方程两边可以同乘以(
)
A.
3y-6
B.
3y
C.
3
(3y-6)
D.
3y
(y-2)
1.下列关于x的方程中,是分式方程的是( )
A.
B.
C.
D.
D
小试牛刀
3.
解分式方程
时,去分母后得到的整式方程是
(
)
A.2(x-8)+5x=16(x-7)
B.2(x-8)+5x=8
C.2(x-8)-5x=16(x-7)
D.2(x-8)-5x=8
A
4.若关于x的分式方程
无解,则m的值为
(
)
A.-1,5
B.1
C.-1.5或2
D.-0.5或-1.5
D
小试牛刀
5.解方程:
解:方程两边乘
(x+3)(x-3)得,
解得,
(x-2)(x-3)-3
(x+3)=(x+3)
(x-3)
检验:当
时,
(x+3)
(x-3)≠0.
所以,原分式方程的解为
.
小试牛刀
6、
课堂总结
今天我们收获了哪些知识?
1.什么是分式方程?
2.解分式方程的一般步骤是什么?
3.分式方程为什么是检验?
课后作业
教材152页练习题.
https://www.21cnjy.com/help/help_extract.php
人教版
八年级数学上
15.3分式方程
---第一课时
教学目标
1.掌握解分式方程的基本思路和解法.(重点)
2.理解分式方程时可能无解的原因.(难点)
合作探究---分式方程的概念
一艘轮船在静水中的最大航速为30
km/h,它沿江以最大航速顺流航行90
km所用时间,与以最大航速逆流航行60
km所用时间相等,江水的流速为多少?
题目中相等的数量关系是:
解:设江水的流速为v
km/h.
依题意得:
仔细观察这个方程,未知数的位置有什么特点?
分式的定义:分母中含未知数的方程叫做分式方程.
合作探究---分式方程的概念
判一判:
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
知识点拨:判断一个方程是否为分式方程,主要是看分母中是否含有未知数(注意:π不是未知数).
合作探究---分式方程的解法
问题1:你能试着解这个分式方程吗?
思考2:如何去分母?
思考3:在方程两边乘什么样的式子才能把每一个分母都约去?
思考4:这样做的依据是什么?
思考1:能否将它转化为整式方程呢?
合作探究---分式方程的解法
解:方程①两边同乘(30+x)(30-x),得:
检验:将x=6代入原分式方程中,
左边=
=右边,
因此x=6是原分式方程的解.
90(30-x)=60(30+x),
解得:
x=6.
x=6是原分式方程的解吗?
答:江水的流速为6km/h.
知识点拨:解分式方程的基本思路:是将分式方程化为整式方程,具体做法是“去分母”
即方程两边同乘最简公分母.这也是解分式方程的一般方法.
针对训练
解:方程两边乘最简公分母
(x+5)(x-5)得,
解得,x=5
x+5=10
检验:把x
=
5
代入原方程中,发现x-5和x2-25的值都为0,相应的分式无意义,因此x=5虽是方程x+5=10的解,但不是原分式方程
的解.实际上,这个分式方程无解.
解分式方程:
合作探究
问题2
:上面两个分式方程中,为什么
去分母后得到的整式方程的解就是它的解,而
去分母后得到的整式方程的解,却不是原分式方程的解呢?
合作探究
我们来观察去分母的过程:
解:方程两边都乘
(30+v)(30-v)得,
解得,v=6
90(30-v)=60(30+v)
解:方程两边都乘
(x+5)(x-5)得,
解得,
x=5
x+5=10
当v=6时,
(30+v)(30-v)≠0
当x=5时,
(x+5)(x-5)=0
整式方程的解与分式方程的解相同
整式方程的解不是分式方程的解
真相揭秘:
第一个分式方程两边同乘了不为0的式子,所得整式方程的解与分式方程的解相同.
真相揭秘:
第二个分式方程两边同乘了等于0的式子,所得整式方程的解与分式方程的解不相同.
合作探究
解分式方程时,去分母后所得整式方程的解有可能使原方程的分母为0,所以分式方程的解必须检验.
怎样检验?
这个整式方程的解是不是原分式的解呢?
分式方程解的检验------必不可少的步骤!
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
典例精析
例1:解方程
解:(1)方程两边乘
x(x-3)得,
解得,
2x=3x-9
x=9
检验:当x=9时,
x(x-3)≠0.
所以,原分式方程的解为x=9.
(2)方程两边同乘以
(x-1)
(x+2)
,
得
x(x+2)-(x-1)(x+2)=3
解得
,
检验:当x
=
1
时,(x-1)
(x+2)=0,因此x
=1不是原分式方程的解.
x
=
1
所以,原分式方程无解.
归纳总结
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
x=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分母为0
小试牛刀
D
2.
要把方程
化为整式方程,方程两边可以同乘以(
)
A.
3y-6
B.
3y
C.
3
(3y-6)
D.
3y
(y-2)
1.下列关于x的方程中,是分式方程的是( )
A.
B.
C.
D.
D
小试牛刀
3.
解分式方程
时,去分母后得到的整式方程是
(
)
A.2(x-8)+5x=16(x-7)
B.2(x-8)+5x=8
C.2(x-8)-5x=16(x-7)
D.2(x-8)-5x=8
A
4.若关于x的分式方程
无解,则m的值为
(
)
A.-1,5
B.1
C.-1.5或2
D.-0.5或-1.5
D
小试牛刀
5.解方程:
解:方程两边乘
(x+3)(x-3)得,
解得,
(x-2)(x-3)-3
(x+3)=(x+3)
(x-3)
检验:当
时,
(x+3)
(x-3)≠0.
所以,原分式方程的解为
.
小试牛刀
6、
课堂总结
今天我们收获了哪些知识?
1.什么是分式方程?
2.解分式方程的一般步骤是什么?
3.分式方程为什么是检验?
课后作业
教材152页练习题.
https://www.21cnjy.com/help/help_extract.php
