人教版数学九年级下册数学:第29章 投影与视图 同步练习(word版,附答案)
文档属性
| 名称 | 人教版数学九年级下册数学:第29章 投影与视图 同步练习(word版,附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 358.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 21:30:01 | ||
图片预览


文档简介
第二十九章 投影与视图
29.1 投影
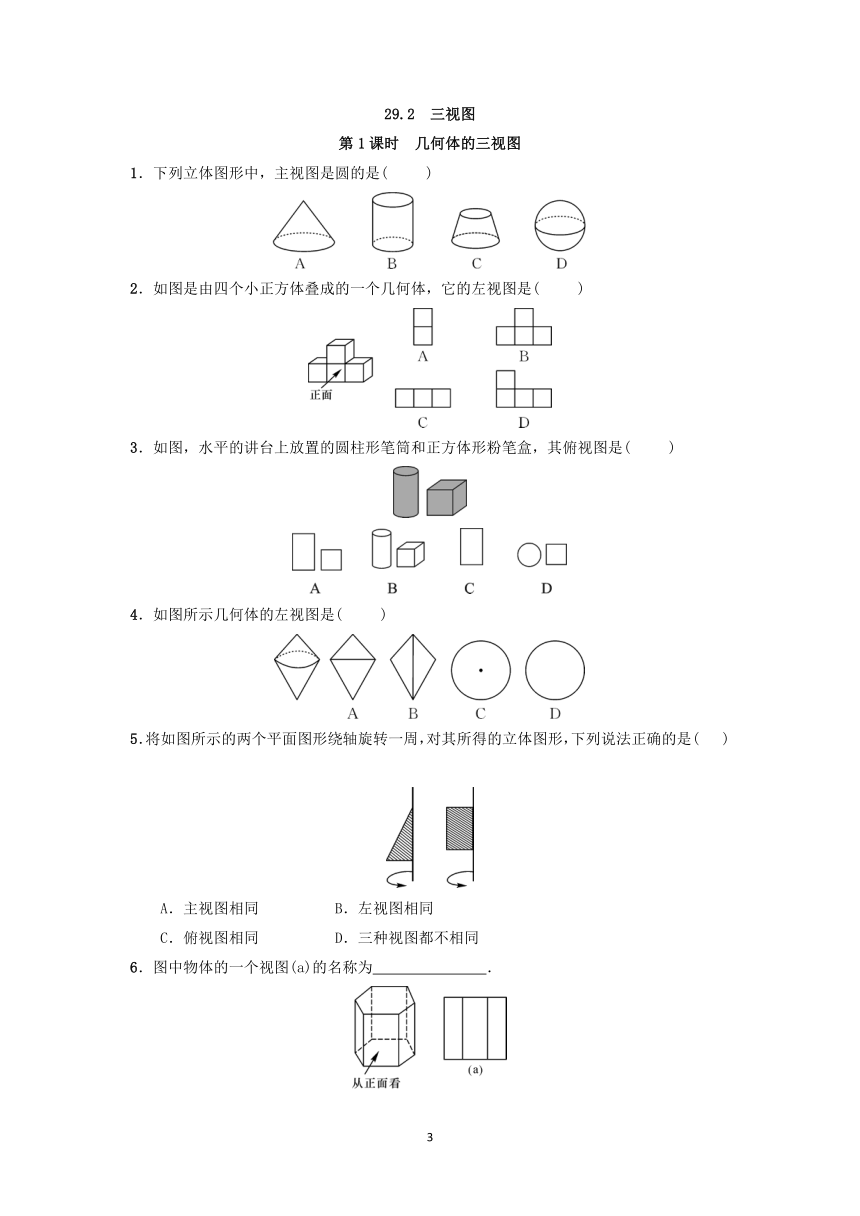
1.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
2.小飞晚上到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定地说,广场上的大灯泡一定位于两人 .
3.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD B.AB≤CD
C.AB>CD D.AB≥CD
4.如图,如果在阳光下你的身影的方向是北偏东60°方向,那么太阳相对于你的方向是( )
A.南偏西60° B.南偏西30°
C.北偏东60° D.北偏东30°
5.如图所示,右面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是( )
6.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示).
7.如图,已知线段AB=2 cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.
29.2 三视图
第1课时 几何体的三视图
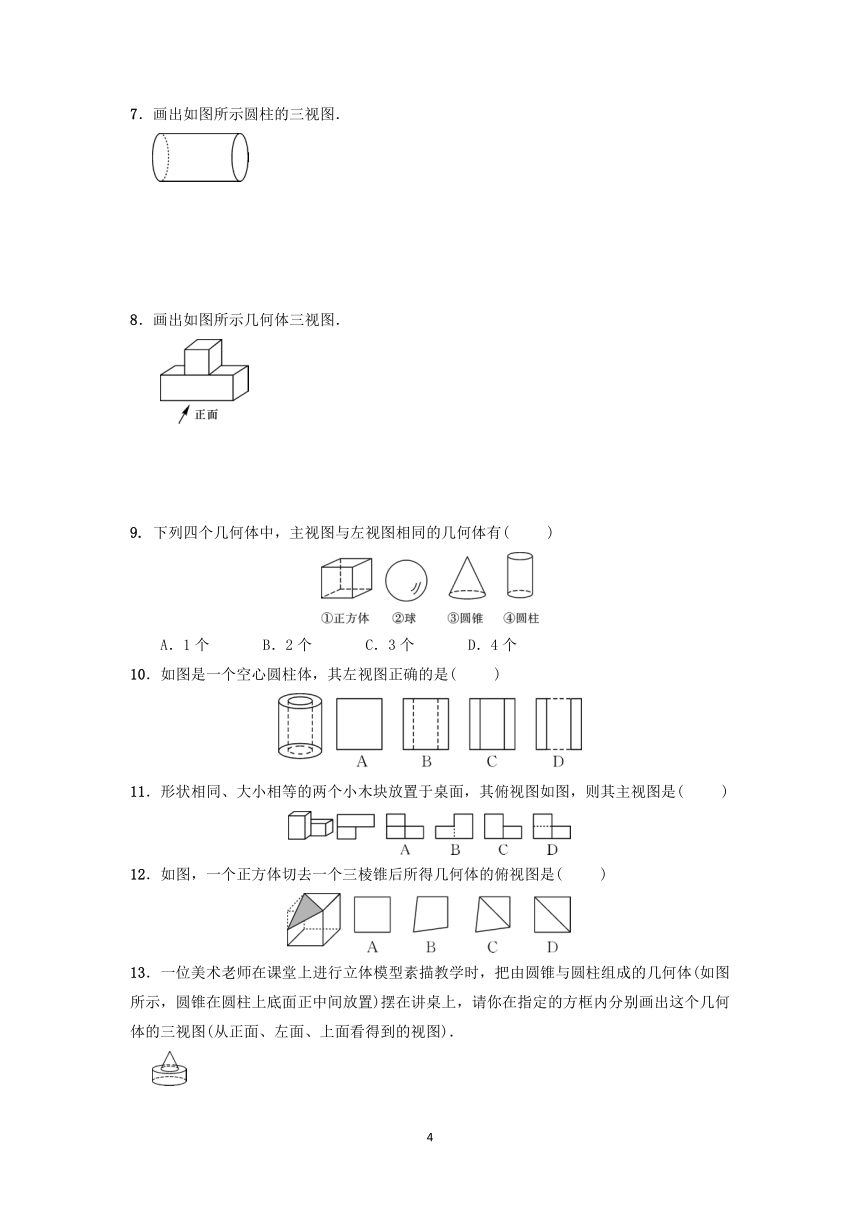
1.下列立体图形中,主视图是圆的是( )
2.如图是由四个小正方体叠成的一个几何体,它的左视图是( )
3.如图,水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是( )
4.如图所示几何体的左视图是( )
5.将如图所示的两个平面图形绕轴旋转一周,对其所得的立体图形,下列说法正确的是( )
A.主视图相同 B.左视图相同
C.俯视图相同 D.三种视图都不相同
6.图中物体的一个视图(a)的名称为 .
7.画出如图所示圆柱的三视图.
8.画出如图所示几何体三视图.
9. 下列四个几何体中,主视图与左视图相同的几何体有( )
A.1个 B.2个 C.3个 D.4个
10.如图是一个空心圆柱体,其左视图正确的是( )
11.形状相同、大小相等的两个小木块放置于桌面,其俯视图如图,则其主视图是( )
12.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
13.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图(从正面、左面、上面看得到的视图).
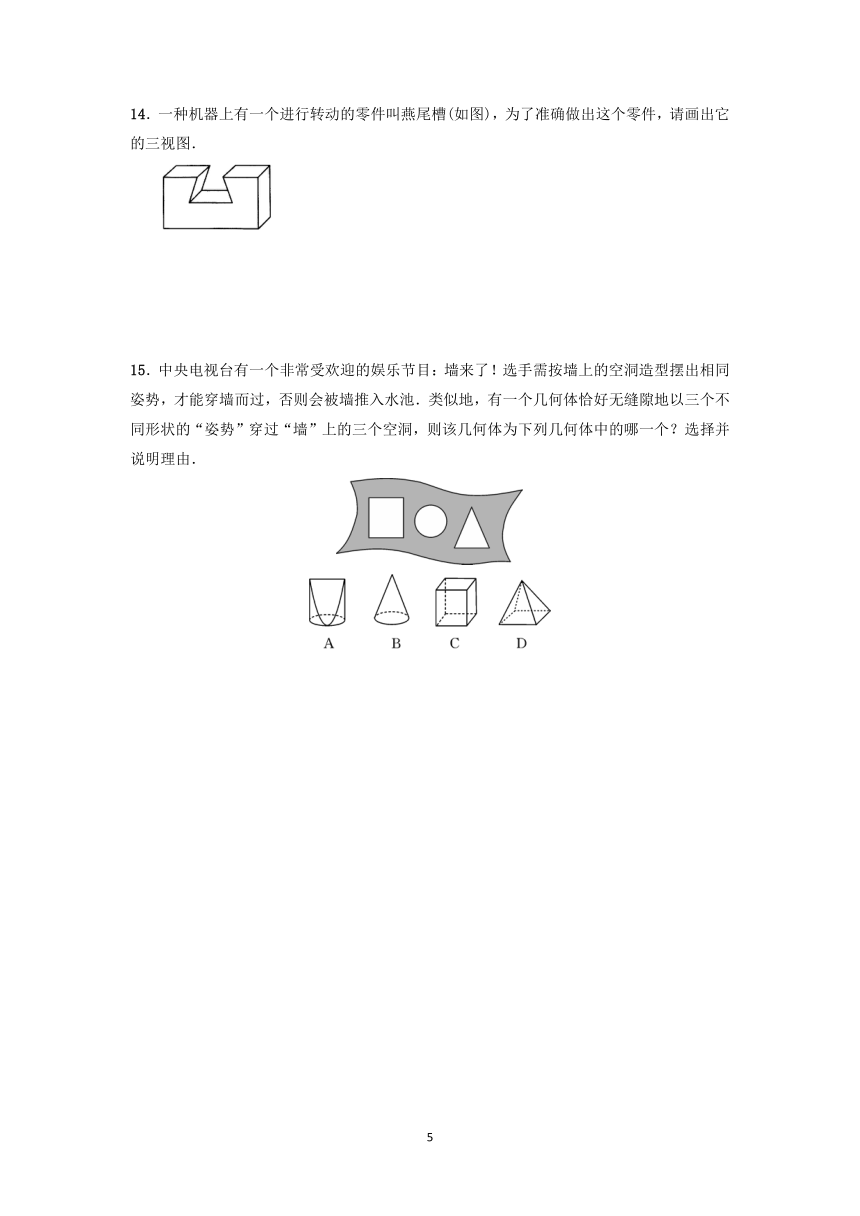
14.一种机器上有一个进行转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图.
15.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下列几何体中的哪一个?选择并说明理由.
第2课时 由三视图确定几何体
1.如图是某几何体的三视图,则这个几何体是( )
A.棱柱 B.圆柱
C.棱锥 D.圆锥
2.一个几何体的三视图如图所示,这个几何体是( )
A.圆柱 B.棱柱
C.圆锥 D.球
3.如图所示,所给的三视图表示的几何体是( )
A.圆锥 B.正三棱锥
C.正四棱锥 D.正三棱柱
4.如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上方小正方体的个数,这个立体图形的左视图是( )
5.图中的三视图所对应的几何体是( )
6.已知一个正棱柱的俯视图和左视图如图,则其主视图为( )
7.某几何体的三视图如图所示,则组成该几何体共用了小方块( )
A.12块 B.9块 C.7块 D.6块
8.如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体不可能是( )
A.6个 B.7个 C.8个 D.9个
第3课时 由三视图确定几何体的表面积或体积
1.如图是一个几何体的三视图,根据图中提供的数据(单位: cm)可求得这个几何体的体积为( )
A.2 cm3 B.3 cm3 C.6 cm3 D.8 cm3
2.如图是一几何体的三视图,由图中数据计算此几何体的侧面积为 .(结果保留π)
3.如图是某工件的三视图,求此工件的全面积.
4.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积,结果为 cm2.(结果可保留根号)
42214803206755.一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
6.如图是一个几何体的三视图(单位:cm).
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个路线的最短长度.
参考答案:
第二十九章 投影与视图
29.1 投影
1.B
2. 中间的上方.
3.D
4.A
5.D
6.
解:如图所示.
7.解:(1)点C为所求的投影.
(2)线段CD为所求的投影,CD=2 cm.
(3)线段CD为所求的投影,CD=2cos30°= cm.
29.2 三视图
第1课时 几何体的三视图
1.D
2.A
3.D
4.A
5.D
6. 主视图.
7.解:如图所示.
8.解:如图所示.
9. D
10.B
11.D
12.D
13.
解:如图.
14.解:如图.
15.解:比较各几何体的三视图,考虑是否有长方形,圆及三角形即可.对于A,三视图分别为长方形、三角形、圆(含直径),符合题意;对于B,三视图分别为三角形、三角形、圆(含圆心),不符合题意;对于C,三视图分别为正方形、正方形、正方形,不符合题意;对于D,三视图分别为三角形、三角形、矩形(含对角线),不符合题意;故选A.
第2课时 由三视图确定几何体
1.D
2.A
3.D
4.B
5.B
6.D
7.D
8.D 提示:如图,根据左视图可以推测d=e=1,a,b,c中至少有一个为2.
当a,b,c中一个为2时,小立方体的个数为:1+1+2+1+1=6;
当a,b,c中两个为2时,小立方体的个数为:1+1+2+2+1=7;
当a,b,c三个都为2时,小立方体的个数为:1+1+2+2+2=8.
所以小立方体的个数可能为6个、7个或8个.
故选D.
第3课时 由三视图确定几何体的表面积或体积
1.B
2. 10π.
3.解:由三视图可知,该工件为底面半径为10 cm、高为30 cm的圆锥体.
圆锥的母线长为=10(cm),
圆锥的侧面积为×20π×10=
100π(cm2),
圆锥的底面积为102π=100π(cm2),
圆锥的全面积为100π+100π=100(1+)π(cm2).
4.(75+360)
5.解:该几何体的形状是直四棱柱,由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm.
∴菱形的边长为=(cm),棱柱的侧面积为×8×4=80(cm2).
6.解:(1)圆锥.
(2)表面积S=S扇形+S圆=πrl+πr2=12π+4π=16π(cm2).
(3)如图将圆锥侧面展开,线段BD为所求的最短长度.
由条件,得∠BAB′=120°,C为弧BB′的中点,
∴BD=3(cm).
29.1 投影
1.小明拿一个等边三角形木框在太阳下玩耍,发现等边三角形木框在地面上的投影不可能是( )
2.小飞晚上到广场去玩,他发现有两人的影子一个向东,一个向西,于是他肯定地说,广场上的大灯泡一定位于两人 .
3.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD B.AB≤CD
C.AB>CD D.AB≥CD
4.如图,如果在阳光下你的身影的方向是北偏东60°方向,那么太阳相对于你的方向是( )
A.南偏西60° B.南偏西30°
C.北偏东60° D.北偏东30°
5.如图所示,右面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是( )
6.如图,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD.
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);
(2)画出小华此时在路灯下的影子(用线段EF表示).
7.如图,已知线段AB=2 cm,投影面为P,太阳光线与地面垂直.
(1)当AB垂直于投影面P时(如图1),请画出线段AB的投影;
(2)当AB平行于投影面P时(如图2),请画出它的投影,并求出正投影的长;
(3)在(2)的基础上,点A不动,线段AB绕点A在垂直于投影面P的平面内逆时针旋转30°,请在图3中画出线段AB的正投影,并求出其正投影长.
29.2 三视图
第1课时 几何体的三视图
1.下列立体图形中,主视图是圆的是( )
2.如图是由四个小正方体叠成的一个几何体,它的左视图是( )
3.如图,水平的讲台上放置的圆柱形笔筒和正方体形粉笔盒,其俯视图是( )
4.如图所示几何体的左视图是( )
5.将如图所示的两个平面图形绕轴旋转一周,对其所得的立体图形,下列说法正确的是( )
A.主视图相同 B.左视图相同
C.俯视图相同 D.三种视图都不相同
6.图中物体的一个视图(a)的名称为 .
7.画出如图所示圆柱的三视图.
8.画出如图所示几何体三视图.
9. 下列四个几何体中,主视图与左视图相同的几何体有( )
A.1个 B.2个 C.3个 D.4个
10.如图是一个空心圆柱体,其左视图正确的是( )
11.形状相同、大小相等的两个小木块放置于桌面,其俯视图如图,则其主视图是( )
12.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
13.一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图(从正面、左面、上面看得到的视图).
14.一种机器上有一个进行转动的零件叫燕尾槽(如图),为了准确做出这个零件,请画出它的三视图.
15.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为下列几何体中的哪一个?选择并说明理由.
第2课时 由三视图确定几何体
1.如图是某几何体的三视图,则这个几何体是( )
A.棱柱 B.圆柱
C.棱锥 D.圆锥
2.一个几何体的三视图如图所示,这个几何体是( )
A.圆柱 B.棱柱
C.圆锥 D.球
3.如图所示,所给的三视图表示的几何体是( )
A.圆锥 B.正三棱锥
C.正四棱锥 D.正三棱柱
4.如图是由几个相同小正方体组成的立体图形的俯视图,图上的数字表示该位置上方小正方体的个数,这个立体图形的左视图是( )
5.图中的三视图所对应的几何体是( )
6.已知一个正棱柱的俯视图和左视图如图,则其主视图为( )
7.某几何体的三视图如图所示,则组成该几何体共用了小方块( )
A.12块 B.9块 C.7块 D.6块
8.如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体不可能是( )
A.6个 B.7个 C.8个 D.9个
第3课时 由三视图确定几何体的表面积或体积
1.如图是一个几何体的三视图,根据图中提供的数据(单位: cm)可求得这个几何体的体积为( )
A.2 cm3 B.3 cm3 C.6 cm3 D.8 cm3
2.如图是一几何体的三视图,由图中数据计算此几何体的侧面积为 .(结果保留π)
3.如图是某工件的三视图,求此工件的全面积.
4.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积,结果为 cm2.(结果可保留根号)
42214803206755.一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的形状,并根据图中所给的数据求出它的侧面积.
6.如图是一个几何体的三视图(单位:cm).
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体中的点B出发,沿表面爬到AC的中点D,请你求出这个路线的最短长度.
参考答案:
第二十九章 投影与视图
29.1 投影
1.B
2. 中间的上方.
3.D
4.A
5.D
6.
解:如图所示.
7.解:(1)点C为所求的投影.
(2)线段CD为所求的投影,CD=2 cm.
(3)线段CD为所求的投影,CD=2cos30°= cm.
29.2 三视图
第1课时 几何体的三视图
1.D
2.A
3.D
4.A
5.D
6. 主视图.
7.解:如图所示.
8.解:如图所示.
9. D
10.B
11.D
12.D
13.
解:如图.
14.解:如图.
15.解:比较各几何体的三视图,考虑是否有长方形,圆及三角形即可.对于A,三视图分别为长方形、三角形、圆(含直径),符合题意;对于B,三视图分别为三角形、三角形、圆(含圆心),不符合题意;对于C,三视图分别为正方形、正方形、正方形,不符合题意;对于D,三视图分别为三角形、三角形、矩形(含对角线),不符合题意;故选A.
第2课时 由三视图确定几何体
1.D
2.A
3.D
4.B
5.B
6.D
7.D
8.D 提示:如图,根据左视图可以推测d=e=1,a,b,c中至少有一个为2.
当a,b,c中一个为2时,小立方体的个数为:1+1+2+1+1=6;
当a,b,c中两个为2时,小立方体的个数为:1+1+2+2+1=7;
当a,b,c三个都为2时,小立方体的个数为:1+1+2+2+2=8.
所以小立方体的个数可能为6个、7个或8个.
故选D.
第3课时 由三视图确定几何体的表面积或体积
1.B
2. 10π.
3.解:由三视图可知,该工件为底面半径为10 cm、高为30 cm的圆锥体.
圆锥的母线长为=10(cm),
圆锥的侧面积为×20π×10=
100π(cm2),
圆锥的底面积为102π=100π(cm2),
圆锥的全面积为100π+100π=100(1+)π(cm2).
4.(75+360)
5.解:该几何体的形状是直四棱柱,由三视图知,棱柱底面菱形的对角线长分别为4 cm,3 cm.
∴菱形的边长为=(cm),棱柱的侧面积为×8×4=80(cm2).
6.解:(1)圆锥.
(2)表面积S=S扇形+S圆=πrl+πr2=12π+4π=16π(cm2).
(3)如图将圆锥侧面展开,线段BD为所求的最短长度.
由条件,得∠BAB′=120°,C为弧BB′的中点,
∴BD=3(cm).
