沪科版八年级数学下册第18章 勾股定理单元测试题(Word版 含答案)
文档属性
| 名称 | 沪科版八年级数学下册第18章 勾股定理单元测试题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 248.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 22:52:26 | ||
图片预览




文档简介
第18章 勾股定理
一、选择题(每题4分,共40分)
1.下列几组数中,为勾股数的一组是
( )
A.5,6,7
B.3,-4,5
C.0.5,1.2,1.3
D.20,48,52
2.已知a,b,c是三角形的三边长,且满足(a-6)2++|c-10|=0,则该三角形是
( )
A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
3.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草,则他们仅仅少走(假设2步为1
m)
( )
A.2步
B.4步
C.5步
D.10步
第3题图
第5题图
第6题图
4.小明从一根长为6
m的钢条上截取一段,截取的钢条恰好与两根长分别为3
m,5
m的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为
( )
A.4
m
B.
m
C.4
m或
m
D.6
m
5.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是
( )
A.48
B.60
C.76
D.80
6.如图,将两个大小、形状完全相同的△ABC和△A'B'C'拼在一起,其中点A'与点A重合,点C'落在AB边上,连接B'C.若∠ACB=∠A'C'B'=90°,AC=BC=3.则B'C的长为
( )
A.3
B.6
C.3
D.
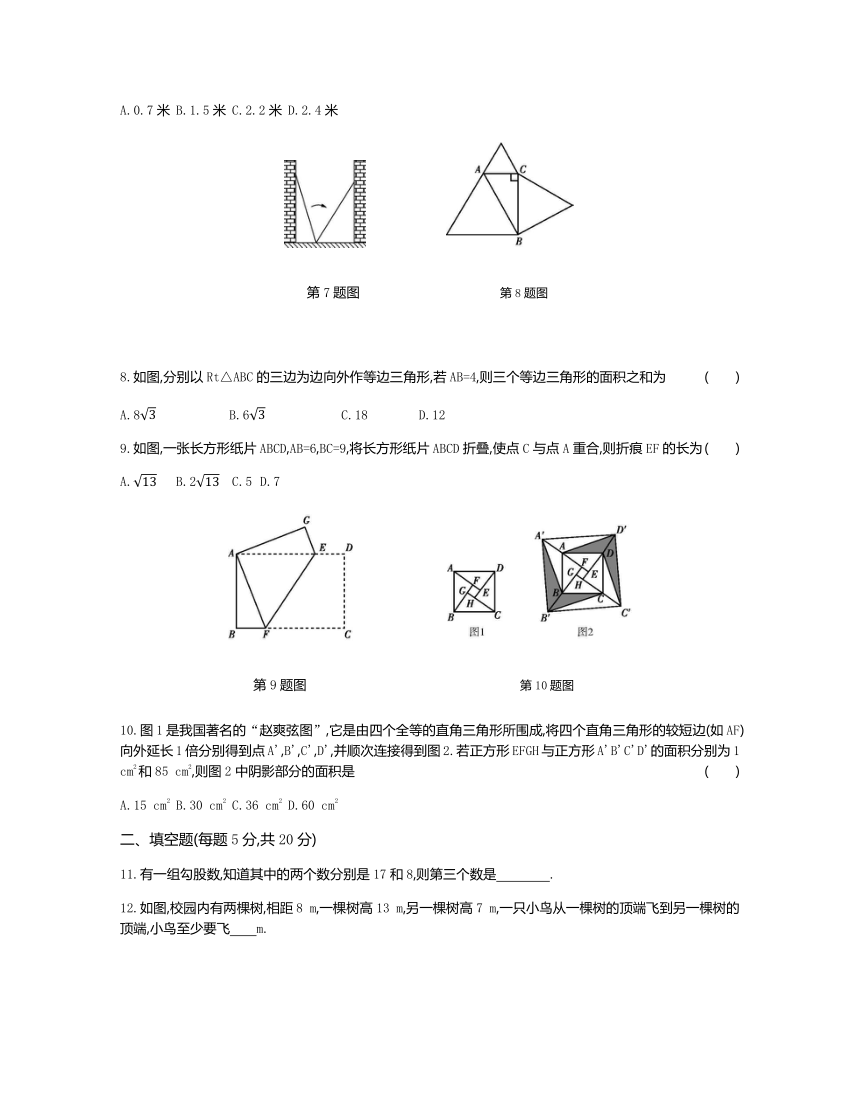
7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为
( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
第7题图
第8题图
8.如图,分别以Rt△ABC的三边为边向外作等边三角形,若AB=4,则三个等边三角形的面积之和为
( )
A.8
B.6
C.18
D.12
9.如图,一张长方形纸片ABCD,AB=6,BC=9,将长方形纸片ABCD折叠,使点C与点A重合,则折痕EF的长为
( )
A.
B.2
C.5
D.7
第9题图
第10题图
10.图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成,将四个直角三角形的较短边(如AF)向外延长1倍分别得到点A',B',C',D',并顺次连接得到图2.若正方形EFGH与正方形A'B'C'D'的面积分别为1
cm2和85
cm2,则图2中阴影部分的面积是
( )
A.15
cm2
B.30
cm2
C.36
cm2
D.60
cm2
二、填空题(每题5分,共20分)
11.有一组勾股数,知道其中的两个数分别是17和8,则第三个数是 .?
12.如图,校园内有两棵树,相距8
m,一棵树高13
m,另一棵树高7
m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 m.?
第12题图
第13题图
第14题图
如图是一个底面周长为24
m,高为5
m的圆柱体,一只蚂蚁沿表面从点A到点B所经过的最短路线
长为 m.?
14.如图,已知1号、4号两个正方形的面积和为7,2号、3号两个正方形的面积和为4,则a,b,c三个正方形的面积和为 .?
三、解答题(共90分)
15.(8分)如图,在△ABC中,AB=10,BC=16,BC边上的中线AD=6.求证:AB=AC.
16.(8分)某校要把一块形状是直角三角形的废地开发为小花园,如图,∠ACB=90°,AC=40
m,BC=30
m.计划建一条水渠CD,且点D在边AB上,已知水渠的造价为3
000元/m,点D距点A多远时,此水渠的造价最低?最低造价是多少?请在图上标出点D.
17.(8分)如图,在由边长为1的小正方形组成的网格图中,四边形ABCD的顶点都在格点上.
(1)求四边形ABCD的周长;
(2)判断AD与DC是否垂直?并说明理由.
18.(8分)如图所示的是一个十字路口,O是两条公路的交点,A,B,C,D表示公路上的四辆车.某一时刻,OC=8
m,AC=17
m,AB=5
m,BD=10
m,求C,D两辆车之间的距离.
19.(10分)如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=5,且AC+BC=6,求AB的长.
20.(10分)有一艘渔船在海上C处作业时发生故障,立即向搜救中心发出求救信号,此时搜救中心的两艘救助轮一号和二号分别位于海上A处和B处,B在A的正东方向,且距A
100海里.测得点C在A的南偏东60°方向上,在B的南偏东30°方向上,如图所示.若救助轮一号和二号的速度分别为40海里/时和30海里/时,问搜救中心应派哪艘救助轮才能尽快赶到C处救援?(≈1.7)
21.(12分)如图,点A是5×5网格中的一个格点,图中每个小正方形的边长为1,请在网格中按下列要求操作(顶点都在格点上的多边形为格点多边形):
(1)以点A为其中的一个顶点,在图1中画一个面积等于3的格点直角三角形;
(2)以点A为其中的一个顶点,在图2中画一个面积等于的格点等腰直角三角形;
(3)以点A为其中的一个顶点,在图3中画一个三边边长比为1∶∶,且最长边的长度为5的格点三角形.
22.(12分)在△ABC中,AB=AC,∠BAC=2∠DAE=2α,点D关于直线AE的对称点为F.
(1)如图1,若α=45°,求证:DE2=BD2+CE2;
(2)如图2,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还成立吗?请说明理由.
23.(14分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图1证明勾股定理的过程.
如图1,△ACB≌△DEA,∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,DC,过点D作DF⊥BC交BC的延长线于点F,则DF=EC=b-a.
则S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图2证明勾股定理.
如图2,△ACB≌△AED,∠DAB=90°,求证:a2+b2=c2.
图1
图2
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
C
A
C
A
B
B
11.15 12.10 13.13 14.15
15. 因为AD是BC边上的中线,
所以BD=CD=BC=8,
又因为AB=10,AD=6,所以AD2+BD2=AB2,
所以△ADB是直角三角形,AD⊥BC.
在Rt△ADC中,由勾股定理得AC2=AD2+CD2=62+82=102,
所以AC=10,所以AB=AC.
16. 如图,过点C作CD⊥AB于点D,则点D为所求的点.
在Rt△ABC中,由勾股定理,得AB===50(m).
∵S△ABC=AC·BC=AB·CD,
∴CD===24(m).
在Rt△ACD中,由勾股定理,得AD===32(m).
∵水渠的造价为3
000元/m,
∴水渠的最低造价为3
000×24=72
000(元).
故当点D距点A
32
m时,此水渠的造价最低,最低造价是72
000元.
17. (1)由题意可知AB==3,AD==,DC==2,BC==,
∴四边形ABCD的周长为AB+BC+CD+AD=3++3.
(2)AD⊥DC,理由如下:
连接AC.∵AD=,DC=2,AC=5,∴AD2+CD2=AC2,
∴△ACD是直角三角形,且∠ADC=90°,∴AD⊥DC.
18. 在Rt△AOC中,由勾股定理得OA2+OC2=AC2,
∴OA===15(m),
∴OB=OA+AB=20
m.
在Rt△BOD中,由勾股定理得BD2=OB2+OD2,
∴OD===10
(m),
∴CD=OD-OC=10-8=2(m).
19. 由勾股定理,得AC2+BC2=AB2,
∴由题图可知S1+S2=π×()2+π×()2+×AC×BC-π×()2=(AC2+BC2-AB2)+×AC×BC=×AC×BC,
∵S1+S2=5,
∴AC×BC=10,
∴AB===4.
20. 如图,过点C作CD⊥AB交AB的延长线于点D.
由题意得∠EAC=60°,∠FBC=30°,∴∠1=30°,∠2=60°.
∵∠1+∠BCA=∠2,∴∠BCA=30°,∴∠1=∠BCA,
∴BC=AB=100海里.
在Rt△BDC中,BD=BC=50海里,
∴DC==50
海里,AD=AB+BD=150海里.
在Rt△ADC中,由勾股定理,得AC==100
海里,
∴救助轮一号所用的时间t1==≈4.25(时),
救助轮二号所用的时间t2==≈3.33(时),
∵3.33<4.25,∴搜救中心应派救助轮二号才能尽快赶到C处救援.
21. (1)如图1所示.(画法不唯一)
(2)如图2所示.(画法不唯一)
(3)∵三角形的三边边长比为1∶∶,且最长边的长度为5,∴三边长分别为,,5,满足题意的格点三角形如图3所示.(画法不唯一)
22. (1)∵点D,F关于直线AE对称,
∴AD=AF,DE=EF,∠FAE=∠DAE=α.
∴∠DAF=2α=∠BAC,
∴∠DAF-∠DAC=∠BAC-∠DAC,即∠CAF=∠BAD,
又∵AB=AC,AD=AF,∴△BAD≌△CAF,
∴BD=CF,∠ACF=∠ABD.
∵∠BAC=2α=90°,AB=AC,
∴∠ABD=∠ACB=45°,∴∠ACF=45°,
∴∠ECF=∠ACB+∠ACF=90°,∴EF2=EC2+CF2.
∵BD=CF,DE=EF,∴DE2=BD2+CE2.
(2)成立.理由如下:
∵点D,F关于直线AE对称,
∴AD=AF,DE=EF,∠FAE=∠DAE=α,
∴∠DAF=2α=∠BAC,
∴∠DAF-∠DAC=∠BAC-∠DAC,即∠CAF=∠BAD,
又∵AB=AC,AD=AF,∴△BAD≌△CAF,
∴BD=CF,∠ACF=∠ABD.
∵∠BAC=2α=90°,AB=AC,
∴∠ABD=∠ACB=45°,∴∠ACF=45°,
∴∠ECF=180°-∠ACB-∠ACF=90°,
∴EF2=CF2+CE2.
∵EF=DE,CF=BD,∴DE2=BD2+CE2.
23. 如图,连接BD,BE,过点B作BF⊥DE交DE的延长线于点F,则S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab.
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),
∴ab+b2+ab=ab+c2+a(b-a),
∴a2+b2=c2.
一、选择题(每题4分,共40分)
1.下列几组数中,为勾股数的一组是
( )
A.5,6,7
B.3,-4,5
C.0.5,1.2,1.3
D.20,48,52
2.已知a,b,c是三角形的三边长,且满足(a-6)2++|c-10|=0,则该三角形是
( )
A.等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
3.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草,则他们仅仅少走(假设2步为1
m)
( )
A.2步
B.4步
C.5步
D.10步
第3题图
第5题图
第6题图
4.小明从一根长为6
m的钢条上截取一段,截取的钢条恰好与两根长分别为3
m,5
m的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为
( )
A.4
m
B.
m
C.4
m或
m
D.6
m
5.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是
( )
A.48
B.60
C.76
D.80
6.如图,将两个大小、形状完全相同的△ABC和△A'B'C'拼在一起,其中点A'与点A重合,点C'落在AB边上,连接B'C.若∠ACB=∠A'C'B'=90°,AC=BC=3.则B'C的长为
( )
A.3
B.6
C.3
D.
7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为
( )
A.0.7米
B.1.5米
C.2.2米
D.2.4米
第7题图
第8题图
8.如图,分别以Rt△ABC的三边为边向外作等边三角形,若AB=4,则三个等边三角形的面积之和为
( )
A.8
B.6
C.18
D.12
9.如图,一张长方形纸片ABCD,AB=6,BC=9,将长方形纸片ABCD折叠,使点C与点A重合,则折痕EF的长为
( )
A.
B.2
C.5
D.7
第9题图
第10题图
10.图1是我国著名的“赵爽弦图”,它是由四个全等的直角三角形所围成,将四个直角三角形的较短边(如AF)向外延长1倍分别得到点A',B',C',D',并顺次连接得到图2.若正方形EFGH与正方形A'B'C'D'的面积分别为1
cm2和85
cm2,则图2中阴影部分的面积是
( )
A.15
cm2
B.30
cm2
C.36
cm2
D.60
cm2
二、填空题(每题5分,共20分)
11.有一组勾股数,知道其中的两个数分别是17和8,则第三个数是 .?
12.如图,校园内有两棵树,相距8
m,一棵树高13
m,另一棵树高7
m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 m.?
第12题图
第13题图
第14题图
如图是一个底面周长为24
m,高为5
m的圆柱体,一只蚂蚁沿表面从点A到点B所经过的最短路线
长为 m.?
14.如图,已知1号、4号两个正方形的面积和为7,2号、3号两个正方形的面积和为4,则a,b,c三个正方形的面积和为 .?
三、解答题(共90分)
15.(8分)如图,在△ABC中,AB=10,BC=16,BC边上的中线AD=6.求证:AB=AC.
16.(8分)某校要把一块形状是直角三角形的废地开发为小花园,如图,∠ACB=90°,AC=40
m,BC=30
m.计划建一条水渠CD,且点D在边AB上,已知水渠的造价为3
000元/m,点D距点A多远时,此水渠的造价最低?最低造价是多少?请在图上标出点D.
17.(8分)如图,在由边长为1的小正方形组成的网格图中,四边形ABCD的顶点都在格点上.
(1)求四边形ABCD的周长;
(2)判断AD与DC是否垂直?并说明理由.
18.(8分)如图所示的是一个十字路口,O是两条公路的交点,A,B,C,D表示公路上的四辆车.某一时刻,OC=8
m,AC=17
m,AB=5
m,BD=10
m,求C,D两辆车之间的距离.
19.(10分)如图,阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形,已知S1+S2=5,且AC+BC=6,求AB的长.
20.(10分)有一艘渔船在海上C处作业时发生故障,立即向搜救中心发出求救信号,此时搜救中心的两艘救助轮一号和二号分别位于海上A处和B处,B在A的正东方向,且距A
100海里.测得点C在A的南偏东60°方向上,在B的南偏东30°方向上,如图所示.若救助轮一号和二号的速度分别为40海里/时和30海里/时,问搜救中心应派哪艘救助轮才能尽快赶到C处救援?(≈1.7)
21.(12分)如图,点A是5×5网格中的一个格点,图中每个小正方形的边长为1,请在网格中按下列要求操作(顶点都在格点上的多边形为格点多边形):
(1)以点A为其中的一个顶点,在图1中画一个面积等于3的格点直角三角形;
(2)以点A为其中的一个顶点,在图2中画一个面积等于的格点等腰直角三角形;
(3)以点A为其中的一个顶点,在图3中画一个三边边长比为1∶∶,且最长边的长度为5的格点三角形.
22.(12分)在△ABC中,AB=AC,∠BAC=2∠DAE=2α,点D关于直线AE的对称点为F.
(1)如图1,若α=45°,求证:DE2=BD2+CE2;
(2)如图2,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还成立吗?请说明理由.
23.(14分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明勾股定理.下面是小聪利用图1证明勾股定理的过程.
如图1,△ACB≌△DEA,∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,DC,过点D作DF⊥BC交BC的延长线于点F,则DF=EC=b-a.
则S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b-a),
∴b2+ab=c2+a(b-a),
∴a2+b2=c2.
请参照上述证法,利用图2证明勾股定理.
如图2,△ACB≌△AED,∠DAB=90°,求证:a2+b2=c2.
图1
图2
答案
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
C
A
C
A
B
B
11.15 12.10 13.13 14.15
15. 因为AD是BC边上的中线,
所以BD=CD=BC=8,
又因为AB=10,AD=6,所以AD2+BD2=AB2,
所以△ADB是直角三角形,AD⊥BC.
在Rt△ADC中,由勾股定理得AC2=AD2+CD2=62+82=102,
所以AC=10,所以AB=AC.
16. 如图,过点C作CD⊥AB于点D,则点D为所求的点.
在Rt△ABC中,由勾股定理,得AB===50(m).
∵S△ABC=AC·BC=AB·CD,
∴CD===24(m).
在Rt△ACD中,由勾股定理,得AD===32(m).
∵水渠的造价为3
000元/m,
∴水渠的最低造价为3
000×24=72
000(元).
故当点D距点A
32
m时,此水渠的造价最低,最低造价是72
000元.
17. (1)由题意可知AB==3,AD==,DC==2,BC==,
∴四边形ABCD的周长为AB+BC+CD+AD=3++3.
(2)AD⊥DC,理由如下:
连接AC.∵AD=,DC=2,AC=5,∴AD2+CD2=AC2,
∴△ACD是直角三角形,且∠ADC=90°,∴AD⊥DC.
18. 在Rt△AOC中,由勾股定理得OA2+OC2=AC2,
∴OA===15(m),
∴OB=OA+AB=20
m.
在Rt△BOD中,由勾股定理得BD2=OB2+OD2,
∴OD===10
(m),
∴CD=OD-OC=10-8=2(m).
19. 由勾股定理,得AC2+BC2=AB2,
∴由题图可知S1+S2=π×()2+π×()2+×AC×BC-π×()2=(AC2+BC2-AB2)+×AC×BC=×AC×BC,
∵S1+S2=5,
∴AC×BC=10,
∴AB===4.
20. 如图,过点C作CD⊥AB交AB的延长线于点D.
由题意得∠EAC=60°,∠FBC=30°,∴∠1=30°,∠2=60°.
∵∠1+∠BCA=∠2,∴∠BCA=30°,∴∠1=∠BCA,
∴BC=AB=100海里.
在Rt△BDC中,BD=BC=50海里,
∴DC==50
海里,AD=AB+BD=150海里.
在Rt△ADC中,由勾股定理,得AC==100
海里,
∴救助轮一号所用的时间t1==≈4.25(时),
救助轮二号所用的时间t2==≈3.33(时),
∵3.33<4.25,∴搜救中心应派救助轮二号才能尽快赶到C处救援.
21. (1)如图1所示.(画法不唯一)
(2)如图2所示.(画法不唯一)
(3)∵三角形的三边边长比为1∶∶,且最长边的长度为5,∴三边长分别为,,5,满足题意的格点三角形如图3所示.(画法不唯一)
22. (1)∵点D,F关于直线AE对称,
∴AD=AF,DE=EF,∠FAE=∠DAE=α.
∴∠DAF=2α=∠BAC,
∴∠DAF-∠DAC=∠BAC-∠DAC,即∠CAF=∠BAD,
又∵AB=AC,AD=AF,∴△BAD≌△CAF,
∴BD=CF,∠ACF=∠ABD.
∵∠BAC=2α=90°,AB=AC,
∴∠ABD=∠ACB=45°,∴∠ACF=45°,
∴∠ECF=∠ACB+∠ACF=90°,∴EF2=EC2+CF2.
∵BD=CF,DE=EF,∴DE2=BD2+CE2.
(2)成立.理由如下:
∵点D,F关于直线AE对称,
∴AD=AF,DE=EF,∠FAE=∠DAE=α,
∴∠DAF=2α=∠BAC,
∴∠DAF-∠DAC=∠BAC-∠DAC,即∠CAF=∠BAD,
又∵AB=AC,AD=AF,∴△BAD≌△CAF,
∴BD=CF,∠ACF=∠ABD.
∵∠BAC=2α=90°,AB=AC,
∴∠ABD=∠ACB=45°,∴∠ACF=45°,
∴∠ECF=180°-∠ACB-∠ACF=90°,
∴EF2=CF2+CE2.
∵EF=DE,CF=BD,∴DE2=BD2+CE2.
23. 如图,连接BD,BE,过点B作BF⊥DE交DE的延长线于点F,则S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab.
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b-a),
∴ab+b2+ab=ab+c2+a(b-a),
∴a2+b2=c2.
