人教版数学九年级上册第二十四章:圆 复习学案(无答案)
文档属性
| 名称 | 人教版数学九年级上册第二十四章:圆 复习学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览




文档简介
人教版九年级上册·第二十四章:圆
①圆的有关性质
②点和圆、直线和圆的位置关系
③正多边形和圆
④弧长和扇形面积
【考点分析】
学习圆的定义,理解弧、弦、半圆、直径等有关概念,掌握圆周角定理及其推论.
2.理解圆内接四边形的性质,研究四点不共圆的性质.
3.根据点到圆心的距离、圆的半径大小关、点与圆的位置关系.
4.通过不在同一直线的三点作图画圆、三角形外接三角形,理解三角形的外心概念.
5.
理解切线长的定义,掌握切线长定理,运用切线长解题.
6.
正多边形的有关概念,特殊正多边形的计算
7.
正多边形的半径、中心角、边心距、边长之间关系的正确理解与计算。
8.会利用弧长和扇形面积的计算公式进行计算.
9.会求圆锥的侧面积和全面积,通过公式进行题型解答.
【基础知识】
要点一、圆的定义及性质
1.
圆的定义
:以O为端点(固定点),线段OA绕固定点旋转一周所形成的图形叫做圆
线段OA叫做半径(r).
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
注:圆心【点】确定圆的位置(先),半径【长】确定圆的大小(后);圆是一条封闭曲线。
2.圆的性质
:圆即是一个旋转对称图形(中心对称图形),也是一个轴对称图形
注:①圆有无数条对称轴;
②因为直径是弦,弦又是线段,而对称轴是直线,“圆的对称轴是直径所在的直线”.
要点二、与圆有关的概念
1.
弦:在圆上的任意两点的连接线段叫做圆的弦【直径:经过圆心的弦叫做直径】
弦心距:圆心到弦的距离
注:直径是经过圆心的特俗弦{AB}【弦不一定是直径】{CD}
图示:
2.
弧:在圆上的任意两点的部分叫做圆的圆弧(弧)
半圆:圆内的任意一直径的两端点把圆分成两条弧,每一条弧都叫做半圆;
优弧:大于半圆的弧叫做优弧;劣弧:小于半圆的弧叫做劣弧【弧指的是劣弧】
3.同心圆(圆心相同)与等圆(半径相同)
4.等弧:在同圆或等圆中,能够完全重合的弧叫做等弧.
要点三、垂径定理
1.垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
2.推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
注:
垂径定理
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧
垂径定理
如图,CD是⊙O的直径,AB是⊙O的的弦,若CD⊥AB,则AE=BE,弧AD=弧BD,
弧AC=弧BC
垂径定理的推论
推论1:平分弦的直径垂直于弦,并且平分弦所对的两条弧
推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧
推论3:平分弦所对一条弧的直径,垂直平分弦,且平分弦所对的另一条弧
要点四、弧、弦、圆心角的关系
1.圆心角定义:顶点在圆心的角叫做圆心角【∠COA】
图示:
2.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
3.推论:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
要点五、圆周角
1.圆周角定义:顶点在圆上,并且两边都与圆相交【∠CBA】
图示:
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半
3.圆周角定理的推论:①同弧或等弧所对的圆周角相等
②半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
4.圆内接四边形:
(1)定义:
圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.
(2)推论:圆内接四边形对角互补,一个外角等于它相邻内角的对角.
(3)如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形(这个圆叫做多边形的外接圆)
要点六、点和圆的位置关系
1.点和圆的三种位置关系
点与圆的位置关系
位置
点M(d)与半径r的位置关系
图示
点在圆内
d点在圆外
d>r
点在圆上
d=r
2.三角形的外接圆
过不在同一直线上的三点作圆
作圆,使它经过不同一直线上的三点A、B、C(即作以点A、B、C为顶点的三角形的外接圆)
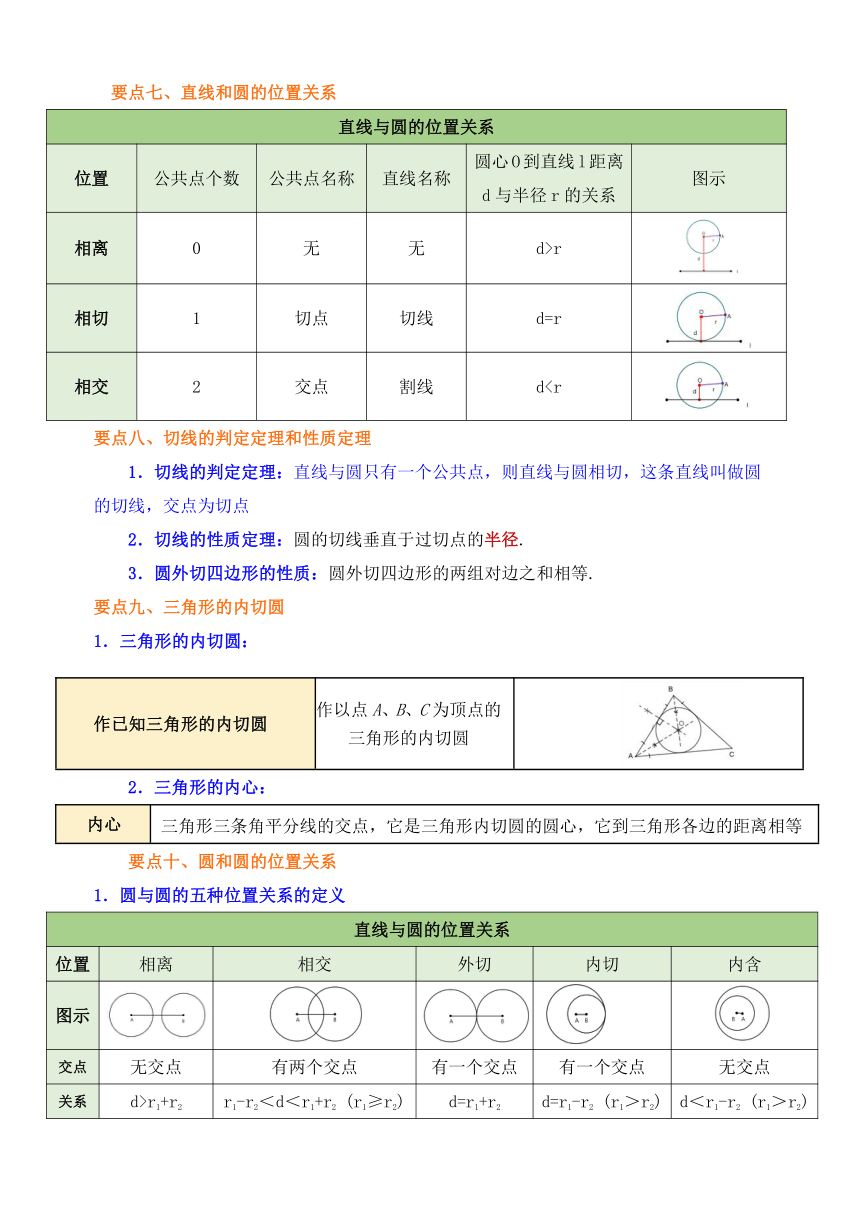
要点七、直线和圆的位置关系
直线与圆的位置关系
位置
公共点个数
公共点名称
直线名称
圆心O到直线l距离d与半径r的关系
图示
相离
0
无
无
d>r
相切
1
切点
切线
d=r
相交
2
交点
割线
d要点八、切线的判定定理和性质定理
1.切线的判定定理:直线与圆只有一个公共点,则直线与圆相切,这条直线叫做圆的切线,交点为切点
2.切线的性质定理:圆的切线垂直于过切点的半径.
3.圆外切四边形的性质:圆外切四边形的两组对边之和相等.
要点九、三角形的内切圆
1.三角形的内切圆:
作已知三角形的内切圆
作以点A、B、C为顶点的三角形的内切圆
2.三角形的内心:
内心
三角形三条角平分线的交点,它是三角形内切圆的圆心,它到三角形各边的距离相等
要点十、圆和圆的位置关系
1.圆与圆的五种位置关系的定义
直线与圆的位置关系
位置
相离
相交
外切
内切
内含
图示
交点
无交点
有两个交点
有一个交点
有一个交点
无交点
关系
d>r1+r2
r1-r2<d<r1+r2
(r1≥r2)
d=r1+r2
d=r1-r2
(r1>r2)
d<r1-r2
(r1>r2)
要点十一、正多边形的概念
1.定义
①中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心
②外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距
2.计算公式 ①正n边形每一个内角的度数是
②正n边形每个中心角的度数是
③正n边形每个外角的度数是
注:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
要点十二、弧长公式
360°的圆心角所对的弧长(圆的周长)公式:
n°的圆心角所对的圆的弧长公式:(弧是圆的一部分)
要点十三、扇形面积公式
1.扇形的定义
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
2.扇形面积公式
360°的圆心角所对的扇形面积(圆面积)公式:
n°的圆心角所对的扇形面积公式:
弧长和扇形面积
弧长的计算
(弧长为
l,圆心角度数为n
,圆的半径为r
)
扇形面积的计算
(弧长为
l,圆心角度数为n
,圆的半径为r
)
圆锥的计算
圆锥的侧面积:
圆锥的全面积:(其中l是圆锥的母线长,r是圆锥的底面半径)
【重点难点】
要点一、圆的定义及性质|要点二、与圆有关的概念
Eg1|2、1.下列图形中,是轴对称图形,但不是中心对称图形的是(
)
Eg1|2、2.在△CBA中,∠A=90°,求证:A,B,C三点在同一个圆上
Eg1|2、3.矩形ABCD的对角线AC,BD相较于点O.求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
要点三、垂径定理
Eg3、1.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是(
)
A.AC=AB
B.∠C=∠BOD
C.∠C=∠B
D.∠A=∠BOD
要点四、弧、弦、圆心角的关系|要点五、圆周角
Eg4、1.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为(
)
A.4
B.5
C.4
D.3
Eg4、2.如图,PA,PB分别与⊙O相切于A,B两点.若∠C=65°,则∠P的度数为(
)
A.65°
B.130°
C.50°
D.100°
要点六\七\十、点和圆的位置关系、直线和圆的位置关系、圆和圆的位置关系
Eg6|7|10、1.已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是(
)
A.点P在圆内
B.点P在圆上
C.点P在圆外
D.不能确定
Eg6|7|10、2.如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是(
)
A.
B.
C.
D.2
Eg6|7|10、3.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC的长为_______.
要点八、切线的判定定理和性质定理
Eg8、1.如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求直径AB的长.
Eg8、2.如图,PA,PB分别与⊙O相切于A,B两点.若∠C=65°,则∠P的度数为(
)
A.65°
B.130°
C.50°
D.100°
要点十一、正多边形的概念
Eg11、1.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为
.
Eg11、2.从如图,A,B,C三点是圆O上的三点,若∠AOC=127°,则∠ABC=
要点十二、弧长公式
Eg12、1.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π B.4π C.5π D.6π
Eg12、2.如果一个扇形的半径是1,弧长是,那么此扇形的圆心角的大小为( )
A.30°
B.45°
C.60°
D.90°
Eg12、3.在半径为6
cm的圆中,60°的圆心角所对的弧长等于____cm(结果保留π).
要点十三、扇形面积公式
Eg13、1.已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是(
)
A.24cm
B.48cm
C.96cm
D.192cm
Eg13、2.在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
Eg13、3.AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是的中点,⊙O的半径为1,求图中阴影部分的面积.
【考点过关】
1.下列命题正确的有( )
①半圆是弧;
②弦是圆上两点之间的部分;
③半径是弦;
④直径是最长的弦;
⑤在同一平面内,到定点的距离等于定长的点都在同一个圆上.
A.1个
B.2个
C.3个
D.4个
2.P是⊙O内的一点,P到⊙O的最小距离为4
cm,最大距离为9
cm,则该⊙O的直径为
A.6.5
cm
B.2.5
cm
C.13
cm
D.无法确定
3.弦CD垂直于⊙O的直径AB,垂足为H,且CD=2,BD=,则AB的长为( )
A.2
B.3
C.4
D.5
【课后作业】
1.下列说法正确的是(
)
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.若两个圆有公共点,则这两个圆相交
2.如图24-1-4所示,已知∠AOB=60°,则△AOB是____三角形.
3.如图,在平行四边形ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若弧EF的长为,则图中阴影部分的面积为
4.如图24-1-23,AB是⊙O的弦,OC⊥AB于点C,连接OA,OB.点P是半径OB上任意一点,连接AP.若OA=5
cm,OC=3
cm,则AP的长度可能是____cm(写出一个符合条件的数值即可).
知识脉络
①圆的有关性质
②点和圆、直线和圆的位置关系
③正多边形和圆
④弧长和扇形面积
【考点分析】
学习圆的定义,理解弧、弦、半圆、直径等有关概念,掌握圆周角定理及其推论.
2.理解圆内接四边形的性质,研究四点不共圆的性质.
3.根据点到圆心的距离、圆的半径大小关、点与圆的位置关系.
4.通过不在同一直线的三点作图画圆、三角形外接三角形,理解三角形的外心概念.
5.
理解切线长的定义,掌握切线长定理,运用切线长解题.
6.
正多边形的有关概念,特殊正多边形的计算
7.
正多边形的半径、中心角、边心距、边长之间关系的正确理解与计算。
8.会利用弧长和扇形面积的计算公式进行计算.
9.会求圆锥的侧面积和全面积,通过公式进行题型解答.
【基础知识】
要点一、圆的定义及性质
1.
圆的定义
:以O为端点(固定点),线段OA绕固定点旋转一周所形成的图形叫做圆
线段OA叫做半径(r).
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
注:圆心【点】确定圆的位置(先),半径【长】确定圆的大小(后);圆是一条封闭曲线。
2.圆的性质
:圆即是一个旋转对称图形(中心对称图形),也是一个轴对称图形
注:①圆有无数条对称轴;
②因为直径是弦,弦又是线段,而对称轴是直线,“圆的对称轴是直径所在的直线”.
要点二、与圆有关的概念
1.
弦:在圆上的任意两点的连接线段叫做圆的弦【直径:经过圆心的弦叫做直径】
弦心距:圆心到弦的距离
注:直径是经过圆心的特俗弦{AB}【弦不一定是直径】{CD}
图示:
2.
弧:在圆上的任意两点的部分叫做圆的圆弧(弧)
半圆:圆内的任意一直径的两端点把圆分成两条弧,每一条弧都叫做半圆;
优弧:大于半圆的弧叫做优弧;劣弧:小于半圆的弧叫做劣弧【弧指的是劣弧】
3.同心圆(圆心相同)与等圆(半径相同)
4.等弧:在同圆或等圆中,能够完全重合的弧叫做等弧.
要点三、垂径定理
1.垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
2.推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
注:
垂径定理
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧
垂径定理
如图,CD是⊙O的直径,AB是⊙O的的弦,若CD⊥AB,则AE=BE,弧AD=弧BD,
弧AC=弧BC
垂径定理的推论
推论1:平分弦的直径垂直于弦,并且平分弦所对的两条弧
推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧
推论3:平分弦所对一条弧的直径,垂直平分弦,且平分弦所对的另一条弧
要点四、弧、弦、圆心角的关系
1.圆心角定义:顶点在圆心的角叫做圆心角【∠COA】
图示:
2.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
3.推论:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等.
要点五、圆周角
1.圆周角定义:顶点在圆上,并且两边都与圆相交【∠CBA】
图示:
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半
3.圆周角定理的推论:①同弧或等弧所对的圆周角相等
②半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
4.圆内接四边形:
(1)定义:
圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.
(2)推论:圆内接四边形对角互补,一个外角等于它相邻内角的对角.
(3)如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形(这个圆叫做多边形的外接圆)
要点六、点和圆的位置关系
1.点和圆的三种位置关系
点与圆的位置关系
位置
点M(d)与半径r的位置关系
图示
点在圆内
d
d>r
点在圆上
d=r
2.三角形的外接圆
过不在同一直线上的三点作圆
作圆,使它经过不同一直线上的三点A、B、C(即作以点A、B、C为顶点的三角形的外接圆)
要点七、直线和圆的位置关系
直线与圆的位置关系
位置
公共点个数
公共点名称
直线名称
圆心O到直线l距离d与半径r的关系
图示
相离
0
无
无
d>r
相切
1
切点
切线
d=r
相交
2
交点
割线
d
1.切线的判定定理:直线与圆只有一个公共点,则直线与圆相切,这条直线叫做圆的切线,交点为切点
2.切线的性质定理:圆的切线垂直于过切点的半径.
3.圆外切四边形的性质:圆外切四边形的两组对边之和相等.
要点九、三角形的内切圆
1.三角形的内切圆:
作已知三角形的内切圆
作以点A、B、C为顶点的三角形的内切圆
2.三角形的内心:
内心
三角形三条角平分线的交点,它是三角形内切圆的圆心,它到三角形各边的距离相等
要点十、圆和圆的位置关系
1.圆与圆的五种位置关系的定义
直线与圆的位置关系
位置
相离
相交
外切
内切
内含
图示
交点
无交点
有两个交点
有一个交点
有一个交点
无交点
关系
d>r1+r2
r1-r2<d<r1+r2
(r1≥r2)
d=r1+r2
d=r1-r2
(r1>r2)
d<r1-r2
(r1>r2)
要点十一、正多边形的概念
1.定义
①中心:一个正多边形的外接圆的圆心叫做这个正多边形的中心
②外接圆的半径叫做正多边形的半径,正多边形每一边所对的圆心角叫做正多边形的中心角,中心到正多边形的一边的距离叫做正多边形的边心距
2.计算公式 ①正n边形每一个内角的度数是
②正n边形每个中心角的度数是
③正n边形每个外角的度数是
注:要熟悉正多边形的基本概念和基本图形,将待解决的问题转化为直角三角形.
要点十二、弧长公式
360°的圆心角所对的弧长(圆的周长)公式:
n°的圆心角所对的圆的弧长公式:(弧是圆的一部分)
要点十三、扇形面积公式
1.扇形的定义
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
2.扇形面积公式
360°的圆心角所对的扇形面积(圆面积)公式:
n°的圆心角所对的扇形面积公式:
弧长和扇形面积
弧长的计算
(弧长为
l,圆心角度数为n
,圆的半径为r
)
扇形面积的计算
(弧长为
l,圆心角度数为n
,圆的半径为r
)
圆锥的计算
圆锥的侧面积:
圆锥的全面积:(其中l是圆锥的母线长,r是圆锥的底面半径)
【重点难点】
要点一、圆的定义及性质|要点二、与圆有关的概念
Eg1|2、1.下列图形中,是轴对称图形,但不是中心对称图形的是(
)
Eg1|2、2.在△CBA中,∠A=90°,求证:A,B,C三点在同一个圆上
Eg1|2、3.矩形ABCD的对角线AC,BD相较于点O.求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
要点三、垂径定理
Eg3、1.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是(
)
A.AC=AB
B.∠C=∠BOD
C.∠C=∠B
D.∠A=∠BOD
要点四、弧、弦、圆心角的关系|要点五、圆周角
Eg4、1.如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为(
)
A.4
B.5
C.4
D.3
Eg4、2.如图,PA,PB分别与⊙O相切于A,B两点.若∠C=65°,则∠P的度数为(
)
A.65°
B.130°
C.50°
D.100°
要点六\七\十、点和圆的位置关系、直线和圆的位置关系、圆和圆的位置关系
Eg6|7|10、1.已知⊙O的半径是4,OP=3,则点P与⊙O的位置关系是(
)
A.点P在圆内
B.点P在圆上
C.点P在圆外
D.不能确定
Eg6|7|10、2.如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是(
)
A.
B.
C.
D.2
Eg6|7|10、3.如图,⊙O是△ABC的外接圆,直径AD=4,∠ABC=∠DAC,则AC的长为_______.
要点八、切线的判定定理和性质定理
Eg8、1.如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求直径AB的长.
Eg8、2.如图,PA,PB分别与⊙O相切于A,B两点.若∠C=65°,则∠P的度数为(
)
A.65°
B.130°
C.50°
D.100°
要点十一、正多边形的概念
Eg11、1.从一个半径为10㎝的圆形纸片上裁出一个最大的正方形,则此正方形的边长为
.
Eg11、2.从如图,A,B,C三点是圆O上的三点,若∠AOC=127°,则∠ABC=
要点十二、弧长公式
Eg12、1.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π B.4π C.5π D.6π
Eg12、2.如果一个扇形的半径是1,弧长是,那么此扇形的圆心角的大小为( )
A.30°
B.45°
C.60°
D.90°
Eg12、3.在半径为6
cm的圆中,60°的圆心角所对的弧长等于____cm(结果保留π).
要点十三、扇形面积公式
Eg13、1.已知一块圆心角为300°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥的底面圆的直径是80cm,则这块扇形铁皮的半径是(
)
A.24cm
B.48cm
C.96cm
D.192cm
Eg13、2.在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.
Eg13、3.AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是的中点,⊙O的半径为1,求图中阴影部分的面积.
【考点过关】
1.下列命题正确的有( )
①半圆是弧;
②弦是圆上两点之间的部分;
③半径是弦;
④直径是最长的弦;
⑤在同一平面内,到定点的距离等于定长的点都在同一个圆上.
A.1个
B.2个
C.3个
D.4个
2.P是⊙O内的一点,P到⊙O的最小距离为4
cm,最大距离为9
cm,则该⊙O的直径为
A.6.5
cm
B.2.5
cm
C.13
cm
D.无法确定
3.弦CD垂直于⊙O的直径AB,垂足为H,且CD=2,BD=,则AB的长为( )
A.2
B.3
C.4
D.5
【课后作业】
1.下列说法正确的是(
)
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.若两个圆有公共点,则这两个圆相交
2.如图24-1-4所示,已知∠AOB=60°,则△AOB是____三角形.
3.如图,在平行四边形ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若弧EF的长为,则图中阴影部分的面积为
4.如图24-1-23,AB是⊙O的弦,OC⊥AB于点C,连接OA,OB.点P是半径OB上任意一点,连接AP.若OA=5
cm,OC=3
cm,则AP的长度可能是____cm(写出一个符合条件的数值即可).
知识脉络
同课章节目录
