【A典学案】冲刺100分 八年级上专题复习第六讲 数据的分析(35张)
文档属性
| 名称 | 【A典学案】冲刺100分 八年级上专题复习第六讲 数据的分析(35张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览










文档简介
第六讲 数据的分析
北师大版 八年级上册
知识清单
1.平均数
(1)算术平均数:一般地,对于 n 个数 ,我们把_______________叫做这 n 个数的算术平均数,简称平均数,记为____________.
(2)加权平均数:实际问题中,一组数据里的各个数据的“_____________”未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“____”
,则所求的带权的平均数称为加权平均数.
辨析比较:算术平均数实质上是加权平均数的一种特殊情况(各项的权相等).
重要程度
权
知识清单
2.中位数
定义:一般地,n 个数据按大小顺序排列,处于____________位置的一个数据(或最中间两个数据的____________)叫做这组数据的中位数.
求法:一组数据中位数只有__________个.把一组数据按大小顺序排列,当数据的个数为_________个时,中位数是最中间两个数据的平均数;数据的个数为__________个时,中位数是最中间的那个数据.
3.众数
一组数据中出现次数___________的那个数据叫做这组数据的众数.
最中间
平均数
1
偶数
奇数
最多
知识清单
一组数据的众数可能有多个,它一定是数组中的某一个或几个数据.
典例精讲
类型之一 与中位数、众数有关的计算
【例 1】为了解居民节约用水的情况,增强居民的节水意识,下表是某个单元的住户当月用水量的调查结果,则关于这 12 户居民月用水量,下列说法错误的是( )
A.中位数是 6 吨 B.众数是 6 吨
C.极差是 8 吨 D.平均数是 5 吨
典例精讲
[解析]表中共有 12 个数据,中位数是排列在第 6 位,第 7 位数据的平均数,为 5 吨;众数是出现次数最多的数据 6;
极差是最大值 10 与最小值 2 之差,为 8 吨;
平均数 (吨).
故选 A.
变式训练
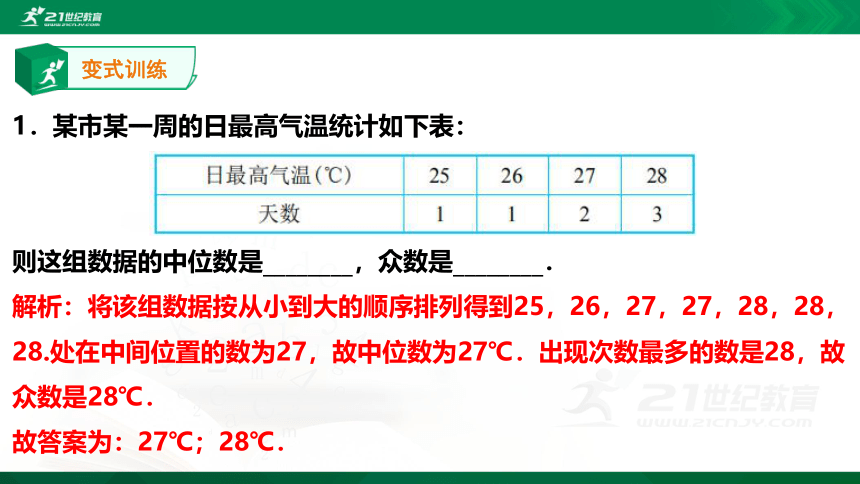
1.某市某一周的日最高气温统计如下表:
则这组数据的中位数是________,众数是________.
解析:将该组数据按从小到大的顺序排列得到25,26,27,27,28,28,28.处在中间位置的数为27,故中位数为27℃.出现次数最多的数是28,故众数是28℃.
故答案为:27℃;28℃.
典例精讲
类型之二 从统计图中求解相关集中趋势的统计量
【例 2】某次夏令营活动,有小学生、初中生、高中生和大学生参加,共 200 人,各类学生人数的扇形统计图如图所示.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元,则平均每人捐款多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)一一记录
典例精讲
下来,则在这组数据中,众数是多少?
[解析](1)参加这次夏令营活动的初中生共有
200×(1-10%-20%-30%)=80(人).
(2)小学生、高中生和大学生的人数分别为200×20%=40(人),200×30%=60(人),200×10%=20(人),
∴平均每人捐款(40×5+80×10+60×15+20×20)÷20=11.5(元).
(3)∵初中生最多,∴众数为 10 元.
变式训练
2.某市发生地震后,某校学生会向全校 1900 名学生发起了捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并将得到的数据绘制成了如图的统计图.
请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为________,图 1 中 m 的值是________;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为 10 元的学生人数.
变式训练
变式训练
解析:(1)50;32.
(2) (元),
∴这组样本数据的平均数是16元;
∵在这组样本数据中,10元出现了16次,出现的次数最多,
∴这组样本数据的众数为10元;
∵将这组样本数据按从小到大的顺序排列,其中处于中间位置的两个数都是15元,有 (元),∴这组样本数据的中位数为15元.
变式训练
(3)∵在50名学生中,捐款金额为10元的学生人数的比例为32%,
∴由样本数据,估计该校1900名学生中捐款金额为10元的学生人数的比例为32%,即1900×32%=608(名).
∴该校本次活动捐款金额为10元的学生约有608名.
典例精讲
类型之三 用平均数、中位数和众数做决策
【例 3】某市实行中考改革,需要根据该市中学生体能的实际状况重新制定中考体育标准,为此抽取了50 名初中毕业的女学生进行一分钟仰卧起坐次数测试,测试情况绘制成表格如下:
(1)求这次测试数据的平均数、众数和中位数.
(2)根据这一数据的特点,你认为该市中考女生一分钟仰卧起坐项目测试的合格标准次数应定为多少较为合适?请简要说明理由.
典例精讲
[解析](1)平均数为:
众数为 48,中位数为 48.
(2)根据(1)的结果,该市中考女生一分钟仰卧起坐项目测试的合格标准次数应定为 48 比较合适,因为每分钟做 48 次对大多数同学来说都能达到.
变式训练
3.某乡镇企业生产部有技术工人 15 人,生产部为了合理制定产品的每月生产定额,统计了这 15 人某月的加工零件个数如下表:
(1)写出这 15 人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为 260 件,你认为这个定额是否合理,为什么?
变式训练
解析:(1)平均数:260件,中位数:240件,众数:240件.
(2)不合理.理由:
因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260件是平均数,但不利于调动多数员工的积极性.把月加工零件数定为240较合理,因为240件既是中位数,又是众数,是大多数人能达到的定额.
典例精讲
类型之四 方差在实际生活中的应用
【例 4】八(2)班组织了一次经典朗读比赛,甲、乙两队各 10 人的比赛成绩(10 分制)如下表:
(1)甲队成绩的中位数是________分,乙队成绩的众数是________分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是 1.4,则成绩较为整齐的是________队.
典例精讲
[解析](1)把甲队的成绩按从小到大的顺序排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是 9.5 分;乙队成绩中 10 出现了 4 次,出现的次数最多,则乙队成绩的众数是 10 分.故答案为 9.5,10.
(2)乙队的平均成绩: (分).
方差:
(3)∵甲队成绩的方差是 1.4,乙队成绩的方差是 1,∴成绩较为整齐的是乙队.故答案为:乙.
变式训练
4.两台机床同时生产直径为 10 mm 的零件,为了检验产品质量,质检员从两台机床生产的产品中各抽出4 件进行测量,结果如下表:
如果你是质检员,在收集到上述数据后,会通过怎样的运算来判断哪台机床生产的零件质量更符合要求?
变式训练
解析:
显然 故机床乙生产的零件质量更符合要求.
区校真题
1.(深外)随着网络的发展,在节日期间长辈们往往用抢微信红包的形式发放红包,下表是某班同学们在春节期间所抢的红包金额进行统计的结果表:
根据表中提供的信息,红包金额的众数和中位数分别是( )
A.16 元,50 元 B.30 元,30 元
C.30 元,40 元 D.30 元,50 元
C
区校真题
2.(南山)在庆祝新中国成立 70 周年的校园歌唱比赛中,11 名参赛同学的成绩各不相同,按照成绩取前5 名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这 11 名同学成绩的( ) A.平均数 B.中位数 C.众数 D.方差
B
区校真题
3.(福田)袁隆平海水稻科研团队为考察最近选育的水稻生长情况,在同一时期,分别从甲、乙、丙三种稻田苗中随机抽取部分稻苗测量苗高(单位:cm),算得它们的方差分别为 ,则下列对苗高的整齐程度描述正确的是( )
A.甲最整齐 B.乙最整齐 C.丙最整齐 D.一样整齐
4.(深实验)某班抽取 6 名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
A.众数是 80 B.中位数是 75 C.平均数是 80 D.极差是 15
A
B
区校真题
5.(南山)一组数据:-1,3,2,x,5,它有唯一的众数是 3,则这组数据的中位数是___________.
6.(龙华)已知 A,B 两种商品在一周内的价格变化如图所示,则 A,B 两种商品中价格较为稳定的是___________.(填“A”“B”或“相同”)
3
B
区校真题
7.(宝安)下表记录了甲、乙、丙、丁四名运动员最近几次 1000 米训练成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择________运动员.
甲
区校真题
8.(罗湖)某校在八年级开展环保知识问卷调查活动,问卷一共 10 道题,八年级(三)班的问卷得分情
况统计图如下图所示:
(1)扇形统计图中,a=______; (2)根据以上统计图中的信息,
①问卷得分的极差是______分;
②问卷得分的众数是______分;
③问卷得分的中位数是______分;
(3)请你求出该班同学的平均分.
区校真题
解析:(1)a=1-20%-30%-20%-16%=14%;
故答案为:14%;
(2)①问卷得分的极差是100-60=40(分),
②90分所占的比例最大,故问卷得分的众数是90分,
③问卷得分的中位数是 =85(分);
故答案为:40;90;85;
(3)该班同学的平均分为:60×14%+70×16%+80×20%+90×30%+100×20%=82.6(分).
区校真题
9.(深外)某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出 5 名选手参加复赛,两个班各选出的 5 名选手的复赛成绩如图所示.
(1)根据图示填写下表:
区校真题
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是 70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定.
解:(1)由图可知爱国班5名选手的复赛成绩为:75,80,85,85,100,
求知班5名选手的复赛成绩为:70,100,100,75,80,
∴爱国班的平均数为(75+80+85+85+100)÷5=85,求知班的中位数为80,爱国班的众数为85.填表如下:
区校真题
故答案为:85,85,80;
(2)爱国班成绩好些.因为两个班复赛成绩的平均数相同,爱国班的中位数高,∴爱国班的成绩好.
(3)爱国班比求知班成绩更平稳一些.理由如下:
∴爱国班比求知班成绩更平稳一些
中考链接
在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),
并绘制成下面的统计图.
(1)本次调查的样本容量是______,这组数据的众数为______元;
(2)求这组数据的平均数;
(3)该校共有 600 名学生参与捐款,请你估计该校学生的捐款总数.
中考链接
解:(1)本次调查的样本容量是6+11+8+5=30,
这组数据的众数为10元.
故答案为:30,10.
(2)这组数据的平均数为 =12(元).
(3)估计该校学生的捐款总数为600×12=7 200(元).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版 八年级上册
知识清单
1.平均数
(1)算术平均数:一般地,对于 n 个数 ,我们把_______________叫做这 n 个数的算术平均数,简称平均数,记为____________.
(2)加权平均数:实际问题中,一组数据里的各个数据的“_____________”未必相同.因而,在计算这组数据的平均数时,往往给每个数据一个“____”
,则所求的带权的平均数称为加权平均数.
辨析比较:算术平均数实质上是加权平均数的一种特殊情况(各项的权相等).
重要程度
权
知识清单
2.中位数
定义:一般地,n 个数据按大小顺序排列,处于____________位置的一个数据(或最中间两个数据的____________)叫做这组数据的中位数.
求法:一组数据中位数只有__________个.把一组数据按大小顺序排列,当数据的个数为_________个时,中位数是最中间两个数据的平均数;数据的个数为__________个时,中位数是最中间的那个数据.
3.众数
一组数据中出现次数___________的那个数据叫做这组数据的众数.
最中间
平均数
1
偶数
奇数
最多
知识清单
一组数据的众数可能有多个,它一定是数组中的某一个或几个数据.
典例精讲
类型之一 与中位数、众数有关的计算
【例 1】为了解居民节约用水的情况,增强居民的节水意识,下表是某个单元的住户当月用水量的调查结果,则关于这 12 户居民月用水量,下列说法错误的是( )
A.中位数是 6 吨 B.众数是 6 吨
C.极差是 8 吨 D.平均数是 5 吨
典例精讲
[解析]表中共有 12 个数据,中位数是排列在第 6 位,第 7 位数据的平均数,为 5 吨;众数是出现次数最多的数据 6;
极差是最大值 10 与最小值 2 之差,为 8 吨;
平均数 (吨).
故选 A.
变式训练
1.某市某一周的日最高气温统计如下表:
则这组数据的中位数是________,众数是________.
解析:将该组数据按从小到大的顺序排列得到25,26,27,27,28,28,28.处在中间位置的数为27,故中位数为27℃.出现次数最多的数是28,故众数是28℃.
故答案为:27℃;28℃.
典例精讲
类型之二 从统计图中求解相关集中趋势的统计量
【例 2】某次夏令营活动,有小学生、初中生、高中生和大学生参加,共 200 人,各类学生人数的扇形统计图如图所示.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元,则平均每人捐款多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)一一记录
典例精讲
下来,则在这组数据中,众数是多少?
[解析](1)参加这次夏令营活动的初中生共有
200×(1-10%-20%-30%)=80(人).
(2)小学生、高中生和大学生的人数分别为200×20%=40(人),200×30%=60(人),200×10%=20(人),
∴平均每人捐款(40×5+80×10+60×15+20×20)÷20=11.5(元).
(3)∵初中生最多,∴众数为 10 元.
变式训练
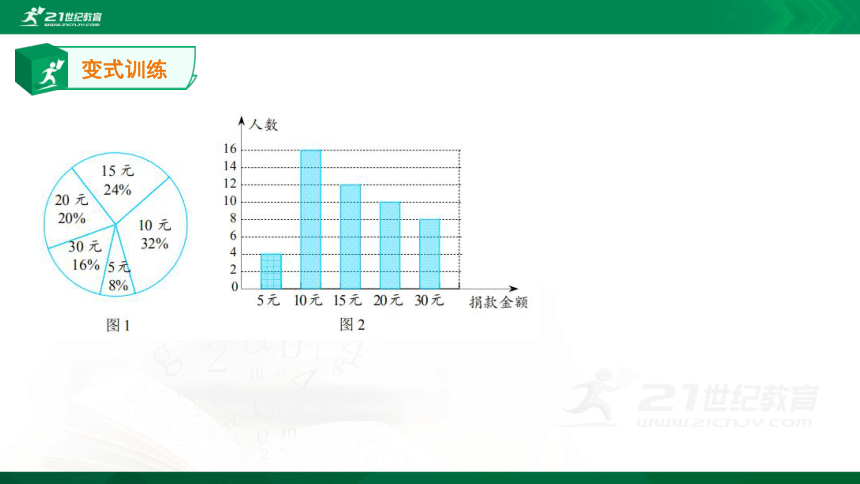
2.某市发生地震后,某校学生会向全校 1900 名学生发起了捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并将得到的数据绘制成了如图的统计图.
请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为________,图 1 中 m 的值是________;
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为 10 元的学生人数.
变式训练
变式训练
解析:(1)50;32.
(2) (元),
∴这组样本数据的平均数是16元;
∵在这组样本数据中,10元出现了16次,出现的次数最多,
∴这组样本数据的众数为10元;
∵将这组样本数据按从小到大的顺序排列,其中处于中间位置的两个数都是15元,有 (元),∴这组样本数据的中位数为15元.
变式训练
(3)∵在50名学生中,捐款金额为10元的学生人数的比例为32%,
∴由样本数据,估计该校1900名学生中捐款金额为10元的学生人数的比例为32%,即1900×32%=608(名).
∴该校本次活动捐款金额为10元的学生约有608名.
典例精讲
类型之三 用平均数、中位数和众数做决策
【例 3】某市实行中考改革,需要根据该市中学生体能的实际状况重新制定中考体育标准,为此抽取了50 名初中毕业的女学生进行一分钟仰卧起坐次数测试,测试情况绘制成表格如下:
(1)求这次测试数据的平均数、众数和中位数.
(2)根据这一数据的特点,你认为该市中考女生一分钟仰卧起坐项目测试的合格标准次数应定为多少较为合适?请简要说明理由.
典例精讲
[解析](1)平均数为:
众数为 48,中位数为 48.
(2)根据(1)的结果,该市中考女生一分钟仰卧起坐项目测试的合格标准次数应定为 48 比较合适,因为每分钟做 48 次对大多数同学来说都能达到.
变式训练
3.某乡镇企业生产部有技术工人 15 人,生产部为了合理制定产品的每月生产定额,统计了这 15 人某月的加工零件个数如下表:
(1)写出这 15 人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为 260 件,你认为这个定额是否合理,为什么?
变式训练
解析:(1)平均数:260件,中位数:240件,众数:240件.
(2)不合理.理由:
因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260件是平均数,但不利于调动多数员工的积极性.把月加工零件数定为240较合理,因为240件既是中位数,又是众数,是大多数人能达到的定额.
典例精讲
类型之四 方差在实际生活中的应用
【例 4】八(2)班组织了一次经典朗读比赛,甲、乙两队各 10 人的比赛成绩(10 分制)如下表:
(1)甲队成绩的中位数是________分,乙队成绩的众数是________分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是 1.4,则成绩较为整齐的是________队.
典例精讲
[解析](1)把甲队的成绩按从小到大的顺序排列为:7,7,8,9,9,10,10,10,10,10,最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是 9.5 分;乙队成绩中 10 出现了 4 次,出现的次数最多,则乙队成绩的众数是 10 分.故答案为 9.5,10.
(2)乙队的平均成绩: (分).
方差:
(3)∵甲队成绩的方差是 1.4,乙队成绩的方差是 1,∴成绩较为整齐的是乙队.故答案为:乙.
变式训练
4.两台机床同时生产直径为 10 mm 的零件,为了检验产品质量,质检员从两台机床生产的产品中各抽出4 件进行测量,结果如下表:
如果你是质检员,在收集到上述数据后,会通过怎样的运算来判断哪台机床生产的零件质量更符合要求?
变式训练
解析:
显然 故机床乙生产的零件质量更符合要求.
区校真题
1.(深外)随着网络的发展,在节日期间长辈们往往用抢微信红包的形式发放红包,下表是某班同学们在春节期间所抢的红包金额进行统计的结果表:
根据表中提供的信息,红包金额的众数和中位数分别是( )
A.16 元,50 元 B.30 元,30 元
C.30 元,40 元 D.30 元,50 元
C
区校真题
2.(南山)在庆祝新中国成立 70 周年的校园歌唱比赛中,11 名参赛同学的成绩各不相同,按照成绩取前5 名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这 11 名同学成绩的( ) A.平均数 B.中位数 C.众数 D.方差
B
区校真题
3.(福田)袁隆平海水稻科研团队为考察最近选育的水稻生长情况,在同一时期,分别从甲、乙、丙三种稻田苗中随机抽取部分稻苗测量苗高(单位:cm),算得它们的方差分别为 ,则下列对苗高的整齐程度描述正确的是( )
A.甲最整齐 B.乙最整齐 C.丙最整齐 D.一样整齐
4.(深实验)某班抽取 6 名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
A.众数是 80 B.中位数是 75 C.平均数是 80 D.极差是 15
A
B
区校真题
5.(南山)一组数据:-1,3,2,x,5,它有唯一的众数是 3,则这组数据的中位数是___________.
6.(龙华)已知 A,B 两种商品在一周内的价格变化如图所示,则 A,B 两种商品中价格较为稳定的是___________.(填“A”“B”或“相同”)
3
B
区校真题
7.(宝安)下表记录了甲、乙、丙、丁四名运动员最近几次 1000 米训练成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择________运动员.
甲
区校真题
8.(罗湖)某校在八年级开展环保知识问卷调查活动,问卷一共 10 道题,八年级(三)班的问卷得分情
况统计图如下图所示:
(1)扇形统计图中,a=______; (2)根据以上统计图中的信息,
①问卷得分的极差是______分;
②问卷得分的众数是______分;
③问卷得分的中位数是______分;
(3)请你求出该班同学的平均分.
区校真题
解析:(1)a=1-20%-30%-20%-16%=14%;
故答案为:14%;
(2)①问卷得分的极差是100-60=40(分),
②90分所占的比例最大,故问卷得分的众数是90分,
③问卷得分的中位数是 =85(分);
故答案为:40;90;85;
(3)该班同学的平均分为:60×14%+70×16%+80×20%+90×30%+100×20%=82.6(分).
区校真题
9.(深外)某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出 5 名选手参加复赛,两个班各选出的 5 名选手的复赛成绩如图所示.
(1)根据图示填写下表:
区校真题
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是 70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定.
解:(1)由图可知爱国班5名选手的复赛成绩为:75,80,85,85,100,
求知班5名选手的复赛成绩为:70,100,100,75,80,
∴爱国班的平均数为(75+80+85+85+100)÷5=85,求知班的中位数为80,爱国班的众数为85.填表如下:
区校真题
故答案为:85,85,80;
(2)爱国班成绩好些.因为两个班复赛成绩的平均数相同,爱国班的中位数高,∴爱国班的成绩好.
(3)爱国班比求知班成绩更平稳一些.理由如下:
∴爱国班比求知班成绩更平稳一些
中考链接
在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),
并绘制成下面的统计图.
(1)本次调查的样本容量是______,这组数据的众数为______元;
(2)求这组数据的平均数;
(3)该校共有 600 名学生参与捐款,请你估计该校学生的捐款总数.
中考链接
解:(1)本次调查的样本容量是6+11+8+5=30,
这组数据的众数为10元.
故答案为:30,10.
(2)这组数据的平均数为 =12(元).
(3)估计该校学生的捐款总数为600×12=7 200(元).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
