【A典学案】冲刺100分 九年级上专题复习第九讲 圆 课件(共43张PPT)
文档属性
| 名称 | 【A典学案】冲刺100分 九年级上专题复习第九讲 圆 课件(共43张PPT) |  | |
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 11:13:09 | ||
图片预览











文档简介
第九讲 圆
北师大版 九年级上册
知识清单
1.确定圆的要素
圆心确定其位置,半径确定其大小.只有圆心没有半径,虽圆的位置固定,但大小不定,因而圆不确定;只有半径而没有圆心,虽圆的大小固定,但圆心的位置不定,因而圆也不确定;只有圆心和半径都固定,圆才被唯一确定.
2.点与圆的位置关系
(1)点与圆的位置关系有三种:点在圆外、点在圆上、点在圆内.
点在圆外,即这个点到圆心的距离_______半径;
大于
知识清单
点在圆上,即这个点到圆心的距离_______半径;
点在圆内,即这个点到圆心的距离_______半径;
判断点与圆的位置关系可由点到圆心的距离 d 与圆的半径 r 来比较得到.
(2)设⊙O 的半径是 r,点 P 到圆心的距离为 d,则有:
d<r 点 P 在圆内;
d=r 点 P 在圆上;
d>r 点 P 在圆外;
[点拨]点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反
等于
小于
知识清单
过来,也可以通过这种数量关系判断点与圆的位置关系.
3.垂径定理
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的________ [注意]①条件中的“弦”可以是直径;
②结论中的“平分弧”指平分弦所对的劣弧、优弧.
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
4.圆的旋转不变性
弧
知识清单
(1)中心对称性:圆是中心对称图形,对称中心为__________.
(2)探究圆中角的一些性质
定理 1:在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
定理 2:在同圆或等圆中,如果两个圆心角、两条弧、________中有一组量相等,那么它们所对应的其余各组量都分别相等.
5.圆周角与圆心角的关系
(1)圆周角的定义:顶点在圆上,且角的两边还与圆相交的角叫做圆周
圆心
两条弦
知识清单
角.
[注意]圆周角有两个特征:角的顶点在圆上,两边在圆内的部分是圆的两条弦.
(2)圆周角与圆心角的关系:一条弧所对的圆周角等于它所对的圆心角的
__________
(3)圆周角的性质
性质:在同圆或等圆中,同弧或等弧所对的圆周角__________.
直径所对的圆周角是 __________;90° 的圆周角所对的弦是__________.
一半
相等
直角
直径
知识清单
[注意]“同弧”指“在一个圆中的同一段弧”;“等弧”指“在同圆或等圆中相等的弧”;“同弧或等弧”不能改为“同弦或等弦”.
6.确定圆的条件
不在同一直线上的三个点确定一个圆.
7.三角形的外接圆
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的___________
8.直线与圆的位置关系
外心
知识清单
知识清单
[易错点]将圆心到直线上某一点的距离看成圆心到直线的距离.
9.圆的切线的性质及判定
性质:圆的切线垂直于经过切点的半径.
判定:经过直线的一端,并且垂直于这条直径的直线是圆的切线.
10.三角形的内切圆
和三角形三边都相切的圆可以作出一个,并且只能作出一个,这个圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的________________
内心
知识清单
[注意]对一个确定的三角形来说,其内切圆有且只有一个,其内心也有且只有一个:内心就是内切圆的圆心.
11.切线长定理
定理:从圆外一点可以引圆的两条____________,它们的____________相等,这一点和圆心的连线平分两条切线的 ____________
12.正多边形和圆
各边相等,各角也相等的多边形叫做正多边形.
把圆分成 n(n≥3)等份:
切线
切线长
夹角
知识清单
(1)依次连接各分点所得的多边形是这个圆的内接正 n 边形.
(2)经过各分点作圆的____________,以相邻切线的交点为顶点的多边形是这个圆的_________正 n 边形.
13.弧长及扇形的面积公式
(1)弧长公式
半径为 R 的圆中,n° 的圆心角所对的弧长 l=____________.
(2)扇形的面积公式
半径为 R,圆心角是 n° 的扇形面积是 S 扇形=____________
切线
外切
知识清单
半径为 R,弧长为 l 的扇形面积是 S 扇形=____________
典例精讲
类型之一 垂径定理
【例 1】已知在以点 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于点 C,D(如图). (1)求证:AC=BD; (2)若大圆的半径 R=10,小圆的半径 r=8,且圆心 O 到直线 AB 的距离为 6,求 AC 的长.
典例精讲
[解析](1)过点 O 作 OE⊥AB. ∵AE=BE,CE=DE,∴BE-DE=AE-CE,即 AC=BD.
(2)∵由(1)可知,OE⊥AB 且 OE⊥CD,连接 OC,OA,
变式训练
1.如图,该某测量发现 8 m 高的旗杆 DE 的影子 EF 落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高 1.6 m,测得其影长为 2.4 m,同时测得 EG 的长为 3 m,HF的长为 1 m,测得拱高(弧 GH 的中点到弦 GH 的距离,即 MN 的长)为 2 m,求小桥所在的圆的半径.
变式训练
解:由相似得 ,解得EF=12(m).
∵EG=3,HF=1,∴GH=EF-EG-HF=8(m).
由垂径定理得:GM= =4(m).又MN=2,
设半径OG=R m,则OM=(R-2)m.
在Rt△OMG中,由勾股定理得:
因此(R-2)2+42=R2,解得R=5.
因此小桥所在圆的半径为5 m.
典例精讲
类型之二 圆的基本性质
【例 2】已知⊙O 的直径为 10,点 A,B,C 在⊙O 上,∠CAB 的平分线交⊙O 于点 D.
(1)如图 1,若 BC 为⊙O 的直径,AB=6,求 AC,BD,CD 的长;
(2)如图 2,若∠CAB=60°,求 BD 的长.
典例精讲
[解析](1)由已知,BC 为⊙O 的直径,
即∠CAB=∠BDC=90°. 在 Rt△CAB 中,BC=10,AB=6.
∵AD 平分∠CAB
∴CD=BD.
在 Rt△BDC 中,BC=10,CD2+BD2=BC2
∴BD2=CD2=50.∴BD=CD=
(2)如图,连接 OB,OD. ∵AD 平分∠CAB,且∠CAB=60°.
典例精讲
∴∠DAB= ∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵⊙O 中,OB=OD.
∴△OBD 是等边三角形.
∵⊙O 的直径为 10,∴OB=5. ∴BD=5.
变式训练
2.如图,AB 是⊙O 的弦,OB=2,∠B=30°,C 是弦 AB 上任意一点(不与点 A,B 重合),连接 CO 并交⊙O 于点 D,连接 AD.
(1)弦长 AB 等于 (结果保留根号)________;
(2)当∠D=20°时,求∠BOD 的度数;
(3)当 AC 的长度为多少时,以 A,C,D 为顶点的三角形与以 B,C,O 为顶点的三角形相似?
变式训练
解:(1)
(2)如图,连接OA.
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D.
又∵∠B=30°,∠D=20°,
∴∠DAB=50°.∴∠BOD=2∠DAB=100°.
(3)∵∠BCO=∠A+∠D,
变式训练
∴∠BCO>∠A,∠BCO>∠D,
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°.
此时∠BOC=60°,∠BOD=120°,
∴∠DAC=60°.∴△DAC∽△BOC.
∵∠BCO=90°,即OC⊥AB,
故当AC的长为 时,以A,C,D为顶点的三角形与以B,C,O为顶点的三角形相似.
典例精讲
类型之三 切线的性质与判定
【例 3】如图,在 Rt△ABC 中,∠ABC=90°,以直角边 AB 为直径作⊙O,交斜边 AC 于点 D,连接BD.
(1)若 AD=3,BD=4,求边 BC 的长;
(2)取 BC 的中点 E,连接 ED,试证明 ED 与⊙O 相切.
典例精讲
[解析](1)∵AB 是直径,∴∠ADB=90°. ∵AD=3,BD=4,∴AB=5.
∵∠ADB=∠ABC,∠A=∠A,
∴△ADB∽△ABC,
(2)证明:连接 OD,在 Rt△BDC 中,
∵点 E 是 BC 的中点,
∴CE=DE,∴∠C=∠CDE. 又 OD=OB,∴∠ODB=∠OBD.
又∵∠OBD+∠DBC=90°,∠C+∠DBC=90°,
典例精讲
∴∠C=∠OBD,∴∠BDO=∠CDE. ∵AB 是直径,∴∠ADB=90°,
∴∠BDC=90°,即∠BDE+∠CDE=90°,
∴∠BDE+∠BDO=90°,即∠ODE=90°, ∴ED 与⊙O 相切.
变式训练
3.如图,在 Rt△ABC 中,∠ABC=90°,以 AB 为直径的⊙O 交 AC 于点 D,过点 D 的切线交 BC 于点 E.
(1)求证: ;
(2)若 tan C= ,DE=2,求 AD 的长.
变式训练
解:(1)证明:连接BD,
∵AB为直径,∠ABC=90°,∴BE切⊙O于点B.
又∵DE切⊙O于点D,∴DE=BE,
∴∠EBD=∠EDB.
∵∠ADB=90°,∴∠EBD+∠C=90°,∠BDE+∠CDE=90°
变式训练
在Rt△ABC中,
又∵△ABD∽△ACB,
典例精讲
类型之四 与圆有关的计算
【例 4】如图,在△ABC 中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC 绕直角顶点 C 顺时针旋转60°得△A′B′C,求点 B 转过的路径长.
[解析]∵在△ABC 中,∠ACB=90°,∠ABC=30°,AB=2,
∵将△ABC 绕直角顶点 C 逆时针旋转 60°得△A′B′C′,
∴∠BCB′=60°.
∴点 B 转过的路径长为:
变式训练
4.如图,在△ABC 中,∠ABC=90°,D 是边 AC 上的一点,连接 BD,使∠A=2∠1,E 是 BC 上的一点,以 BE 为直径的⊙O 经过点 D.
(1)求证:AC 是⊙O 的切线;
(2)若∠A=60°,⊙O 的半径为 2,求阴影部分的面积.(结果保留根号和 π)
变式训练
解:(1)证明:如图,连接OD.
∵OB=OD,∴∠1=∠2.∴∠DOC=2∠1.
∵∠A=2∠1,∴∠A=∠DOC.
∵∠ABC=90°,∴∠A+∠C=90°.
∴∠DOC+∠C=90°.
∴∠ODC=90°.
∵OD为半径,
∴AC是⊙O的切线.
变式训练
(2)∵∠A=∠DOC=60°,OD=2,
区校真题
1.(盐田)如图,AB 是⊙O 的直径,点 C,D 在⊙O 上,∠BOC=110°,
AD∥OC,则∠ABD 等于( )
A.20° B.30°
C.40° D.50°
2.(光明)如图,四边形 ACDB 内接于⊙O,若∠BDC=∠BOC,
则∠BAC 的度数为( )
A.50° B.60°
C.45° D.90°
A
B
区校真题
3.(龙华)如图,在□ABCD 中,∠B=60°,⊙C 的半径为 3,则图中阴影部分的面积是( )
A.π B.2π C.3π D.6π
4.(福田)如图,在 Rt△ABC 中,∠ACB=90°,过点 C 作△ABC 外接圆⊙O 的切线交 AB 的垂直平分线于点 D,AB 的垂直平分线交 AC 于点 E.若 OE=2,AB=8,则 CD=________
C
3
区校真题
5.(南山)如图,在平面直角坐标系中,Rt△ABC 的斜边 AB 在 y 轴上,边 AC 与 x 轴交于点 D,AE 平分∠BAC 交边 BC 于点 E,经过点 A,D,E 的圆的圆心 F 恰好在 y 轴上,⊙F 与 y 轴相交于另一点 G.
(1)求证:BC 是⊙F 的切线;
(2)若点 A,D 的坐标分别为 A(0,-1),D(2,0),求⊙F 的半径;
区校真题
解:(1)证明:连接EF.
∵AE平分∠BAC,∴∠FAE=∠CAE.
∵FA=FE,∴∠FAE=∠FEA.∴∠FEA=∠EAC.∴FE∥AC.
∴∠FEB=∠C=90°,即BC是⊙F的切线.
(2)连接FD.设⊙F的半径为r,则r2=(r-1)2+22.
解得r= .即⊙F的半径为
区校真题
6.(龙岗)如图,已知 AB,CD 为⊙O 的直径,过点 A 作弦 AE 垂直于直径 CD 于 F,点 B 恰好为 的中点,连接 BC,BE.
(1)求证:AE=BC;
(2)若 AE= ,求⊙O 的半径;
(3)在(2)的条件下,求阴影部分的面积.
区校真题
解:(1)证明:连接BD.
∵AB,CD为⊙O的直径,∴∠CBD=∠AEB=90°.
∵点B恰好为 的中点,∴ ∴∠A=∠C.
∵∠ABE=90°-∠A,∠CDB=90°-∠C,
∴∠ABE=∠CDB,∴ ,∴AE=BC.
(2)∵AE⊥CD,
区校真题
在Rt△ABE中, ∴⊙O的半径为2.
(3)连接OE.∵∠A=30°,∴∠EOB=60°.∴△EOB是等边三角形.
中考链接
如图,点 A,B,C 在半径为 8 的⊙O 上,过点 B 作 BD∥AC,交 OA 延长线于点 D.连接 BC,且∠BCA=∠OAC=30°.
(1)求证:BD 是⊙O 的切线;
(2)求图中阴影部分的面积.
中考链接
解:(1)证明:连接OB,交CA于E,
∵∠C=30°,∠C= ∠BOA,∴∠BOA=60°.
∵∠BCA=∠OAC=30°,∴∠AEO=90°.
即OB⊥AC,
∵BD∥AC,∴∠DBE=∠AEO=90°.
∴BD是⊙O的切线;
(2)解:∵AC∥BD,∠OCA=90°,∴∠D=∠CAO=30°.
∵∠OBD=90°,OB=8,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版 九年级上册
知识清单
1.确定圆的要素
圆心确定其位置,半径确定其大小.只有圆心没有半径,虽圆的位置固定,但大小不定,因而圆不确定;只有半径而没有圆心,虽圆的大小固定,但圆心的位置不定,因而圆也不确定;只有圆心和半径都固定,圆才被唯一确定.
2.点与圆的位置关系
(1)点与圆的位置关系有三种:点在圆外、点在圆上、点在圆内.
点在圆外,即这个点到圆心的距离_______半径;
大于
知识清单
点在圆上,即这个点到圆心的距离_______半径;
点在圆内,即这个点到圆心的距离_______半径;
判断点与圆的位置关系可由点到圆心的距离 d 与圆的半径 r 来比较得到.
(2)设⊙O 的半径是 r,点 P 到圆心的距离为 d,则有:
d<r 点 P 在圆内;
d=r 点 P 在圆上;
d>r 点 P 在圆外;
[点拨]点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反
等于
小于
知识清单
过来,也可以通过这种数量关系判断点与圆的位置关系.
3.垂径定理
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的________ [注意]①条件中的“弦”可以是直径;
②结论中的“平分弧”指平分弦所对的劣弧、优弧.
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
4.圆的旋转不变性
弧
知识清单
(1)中心对称性:圆是中心对称图形,对称中心为__________.
(2)探究圆中角的一些性质
定理 1:在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
定理 2:在同圆或等圆中,如果两个圆心角、两条弧、________中有一组量相等,那么它们所对应的其余各组量都分别相等.
5.圆周角与圆心角的关系
(1)圆周角的定义:顶点在圆上,且角的两边还与圆相交的角叫做圆周
圆心
两条弦
知识清单
角.
[注意]圆周角有两个特征:角的顶点在圆上,两边在圆内的部分是圆的两条弦.
(2)圆周角与圆心角的关系:一条弧所对的圆周角等于它所对的圆心角的
__________
(3)圆周角的性质
性质:在同圆或等圆中,同弧或等弧所对的圆周角__________.
直径所对的圆周角是 __________;90° 的圆周角所对的弦是__________.
一半
相等
直角
直径
知识清单
[注意]“同弧”指“在一个圆中的同一段弧”;“等弧”指“在同圆或等圆中相等的弧”;“同弧或等弧”不能改为“同弦或等弦”.
6.确定圆的条件
不在同一直线上的三个点确定一个圆.
7.三角形的外接圆
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的___________
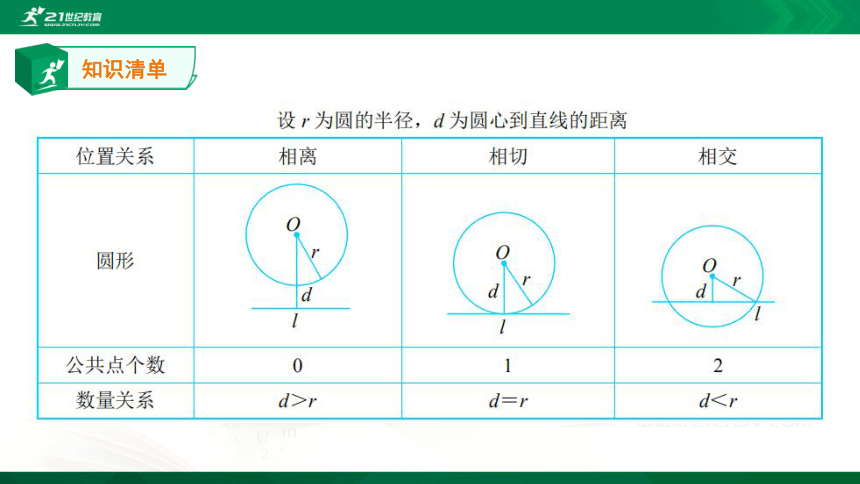
8.直线与圆的位置关系
外心
知识清单
知识清单
[易错点]将圆心到直线上某一点的距离看成圆心到直线的距离.
9.圆的切线的性质及判定
性质:圆的切线垂直于经过切点的半径.
判定:经过直线的一端,并且垂直于这条直径的直线是圆的切线.
10.三角形的内切圆
和三角形三边都相切的圆可以作出一个,并且只能作出一个,这个圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的________________
内心
知识清单
[注意]对一个确定的三角形来说,其内切圆有且只有一个,其内心也有且只有一个:内心就是内切圆的圆心.
11.切线长定理
定理:从圆外一点可以引圆的两条____________,它们的____________相等,这一点和圆心的连线平分两条切线的 ____________
12.正多边形和圆
各边相等,各角也相等的多边形叫做正多边形.
把圆分成 n(n≥3)等份:
切线
切线长
夹角
知识清单
(1)依次连接各分点所得的多边形是这个圆的内接正 n 边形.
(2)经过各分点作圆的____________,以相邻切线的交点为顶点的多边形是这个圆的_________正 n 边形.
13.弧长及扇形的面积公式
(1)弧长公式
半径为 R 的圆中,n° 的圆心角所对的弧长 l=____________.
(2)扇形的面积公式
半径为 R,圆心角是 n° 的扇形面积是 S 扇形=____________
切线
外切
知识清单
半径为 R,弧长为 l 的扇形面积是 S 扇形=____________
典例精讲
类型之一 垂径定理
【例 1】已知在以点 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于点 C,D(如图). (1)求证:AC=BD; (2)若大圆的半径 R=10,小圆的半径 r=8,且圆心 O 到直线 AB 的距离为 6,求 AC 的长.
典例精讲
[解析](1)过点 O 作 OE⊥AB. ∵AE=BE,CE=DE,∴BE-DE=AE-CE,即 AC=BD.
(2)∵由(1)可知,OE⊥AB 且 OE⊥CD,连接 OC,OA,
变式训练
1.如图,该某测量发现 8 m 高的旗杆 DE 的影子 EF 落在了包含一圆弧形小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高 1.6 m,测得其影长为 2.4 m,同时测得 EG 的长为 3 m,HF的长为 1 m,测得拱高(弧 GH 的中点到弦 GH 的距离,即 MN 的长)为 2 m,求小桥所在的圆的半径.
变式训练
解:由相似得 ,解得EF=12(m).
∵EG=3,HF=1,∴GH=EF-EG-HF=8(m).
由垂径定理得:GM= =4(m).又MN=2,
设半径OG=R m,则OM=(R-2)m.
在Rt△OMG中,由勾股定理得:
因此(R-2)2+42=R2,解得R=5.
因此小桥所在圆的半径为5 m.
典例精讲
类型之二 圆的基本性质
【例 2】已知⊙O 的直径为 10,点 A,B,C 在⊙O 上,∠CAB 的平分线交⊙O 于点 D.
(1)如图 1,若 BC 为⊙O 的直径,AB=6,求 AC,BD,CD 的长;
(2)如图 2,若∠CAB=60°,求 BD 的长.
典例精讲
[解析](1)由已知,BC 为⊙O 的直径,
即∠CAB=∠BDC=90°. 在 Rt△CAB 中,BC=10,AB=6.
∵AD 平分∠CAB
∴CD=BD.
在 Rt△BDC 中,BC=10,CD2+BD2=BC2
∴BD2=CD2=50.∴BD=CD=
(2)如图,连接 OB,OD. ∵AD 平分∠CAB,且∠CAB=60°.
典例精讲
∴∠DAB= ∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵⊙O 中,OB=OD.
∴△OBD 是等边三角形.
∵⊙O 的直径为 10,∴OB=5. ∴BD=5.
变式训练
2.如图,AB 是⊙O 的弦,OB=2,∠B=30°,C 是弦 AB 上任意一点(不与点 A,B 重合),连接 CO 并交⊙O 于点 D,连接 AD.
(1)弦长 AB 等于 (结果保留根号)________;
(2)当∠D=20°时,求∠BOD 的度数;
(3)当 AC 的长度为多少时,以 A,C,D 为顶点的三角形与以 B,C,O 为顶点的三角形相似?
变式训练
解:(1)
(2)如图,连接OA.
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D.
又∵∠B=30°,∠D=20°,
∴∠DAB=50°.∴∠BOD=2∠DAB=100°.
(3)∵∠BCO=∠A+∠D,
变式训练
∴∠BCO>∠A,∠BCO>∠D,
∴要使△DAC与△BOC相似,只能∠DCA=∠BCO=90°.
此时∠BOC=60°,∠BOD=120°,
∴∠DAC=60°.∴△DAC∽△BOC.
∵∠BCO=90°,即OC⊥AB,
故当AC的长为 时,以A,C,D为顶点的三角形与以B,C,O为顶点的三角形相似.
典例精讲
类型之三 切线的性质与判定
【例 3】如图,在 Rt△ABC 中,∠ABC=90°,以直角边 AB 为直径作⊙O,交斜边 AC 于点 D,连接BD.
(1)若 AD=3,BD=4,求边 BC 的长;
(2)取 BC 的中点 E,连接 ED,试证明 ED 与⊙O 相切.
典例精讲
[解析](1)∵AB 是直径,∴∠ADB=90°. ∵AD=3,BD=4,∴AB=5.
∵∠ADB=∠ABC,∠A=∠A,
∴△ADB∽△ABC,
(2)证明:连接 OD,在 Rt△BDC 中,
∵点 E 是 BC 的中点,
∴CE=DE,∴∠C=∠CDE. 又 OD=OB,∴∠ODB=∠OBD.
又∵∠OBD+∠DBC=90°,∠C+∠DBC=90°,
典例精讲
∴∠C=∠OBD,∴∠BDO=∠CDE. ∵AB 是直径,∴∠ADB=90°,
∴∠BDC=90°,即∠BDE+∠CDE=90°,
∴∠BDE+∠BDO=90°,即∠ODE=90°, ∴ED 与⊙O 相切.
变式训练
3.如图,在 Rt△ABC 中,∠ABC=90°,以 AB 为直径的⊙O 交 AC 于点 D,过点 D 的切线交 BC 于点 E.
(1)求证: ;
(2)若 tan C= ,DE=2,求 AD 的长.
变式训练
解:(1)证明:连接BD,
∵AB为直径,∠ABC=90°,∴BE切⊙O于点B.
又∵DE切⊙O于点D,∴DE=BE,
∴∠EBD=∠EDB.
∵∠ADB=90°,∴∠EBD+∠C=90°,∠BDE+∠CDE=90°
变式训练
在Rt△ABC中,
又∵△ABD∽△ACB,
典例精讲
类型之四 与圆有关的计算
【例 4】如图,在△ABC 中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC 绕直角顶点 C 顺时针旋转60°得△A′B′C,求点 B 转过的路径长.
[解析]∵在△ABC 中,∠ACB=90°,∠ABC=30°,AB=2,
∵将△ABC 绕直角顶点 C 逆时针旋转 60°得△A′B′C′,
∴∠BCB′=60°.
∴点 B 转过的路径长为:
变式训练
4.如图,在△ABC 中,∠ABC=90°,D 是边 AC 上的一点,连接 BD,使∠A=2∠1,E 是 BC 上的一点,以 BE 为直径的⊙O 经过点 D.
(1)求证:AC 是⊙O 的切线;
(2)若∠A=60°,⊙O 的半径为 2,求阴影部分的面积.(结果保留根号和 π)
变式训练
解:(1)证明:如图,连接OD.
∵OB=OD,∴∠1=∠2.∴∠DOC=2∠1.
∵∠A=2∠1,∴∠A=∠DOC.
∵∠ABC=90°,∴∠A+∠C=90°.
∴∠DOC+∠C=90°.
∴∠ODC=90°.
∵OD为半径,
∴AC是⊙O的切线.
变式训练
(2)∵∠A=∠DOC=60°,OD=2,
区校真题
1.(盐田)如图,AB 是⊙O 的直径,点 C,D 在⊙O 上,∠BOC=110°,
AD∥OC,则∠ABD 等于( )
A.20° B.30°
C.40° D.50°
2.(光明)如图,四边形 ACDB 内接于⊙O,若∠BDC=∠BOC,
则∠BAC 的度数为( )
A.50° B.60°
C.45° D.90°
A
B
区校真题
3.(龙华)如图,在□ABCD 中,∠B=60°,⊙C 的半径为 3,则图中阴影部分的面积是( )
A.π B.2π C.3π D.6π
4.(福田)如图,在 Rt△ABC 中,∠ACB=90°,过点 C 作△ABC 外接圆⊙O 的切线交 AB 的垂直平分线于点 D,AB 的垂直平分线交 AC 于点 E.若 OE=2,AB=8,则 CD=________
C
3
区校真题
5.(南山)如图,在平面直角坐标系中,Rt△ABC 的斜边 AB 在 y 轴上,边 AC 与 x 轴交于点 D,AE 平分∠BAC 交边 BC 于点 E,经过点 A,D,E 的圆的圆心 F 恰好在 y 轴上,⊙F 与 y 轴相交于另一点 G.
(1)求证:BC 是⊙F 的切线;
(2)若点 A,D 的坐标分别为 A(0,-1),D(2,0),求⊙F 的半径;
区校真题
解:(1)证明:连接EF.
∵AE平分∠BAC,∴∠FAE=∠CAE.
∵FA=FE,∴∠FAE=∠FEA.∴∠FEA=∠EAC.∴FE∥AC.
∴∠FEB=∠C=90°,即BC是⊙F的切线.
(2)连接FD.设⊙F的半径为r,则r2=(r-1)2+22.
解得r= .即⊙F的半径为
区校真题
6.(龙岗)如图,已知 AB,CD 为⊙O 的直径,过点 A 作弦 AE 垂直于直径 CD 于 F,点 B 恰好为 的中点,连接 BC,BE.
(1)求证:AE=BC;
(2)若 AE= ,求⊙O 的半径;
(3)在(2)的条件下,求阴影部分的面积.
区校真题
解:(1)证明:连接BD.
∵AB,CD为⊙O的直径,∴∠CBD=∠AEB=90°.
∵点B恰好为 的中点,∴ ∴∠A=∠C.
∵∠ABE=90°-∠A,∠CDB=90°-∠C,
∴∠ABE=∠CDB,∴ ,∴AE=BC.
(2)∵AE⊥CD,
区校真题
在Rt△ABE中, ∴⊙O的半径为2.
(3)连接OE.∵∠A=30°,∴∠EOB=60°.∴△EOB是等边三角形.
中考链接
如图,点 A,B,C 在半径为 8 的⊙O 上,过点 B 作 BD∥AC,交 OA 延长线于点 D.连接 BC,且∠BCA=∠OAC=30°.
(1)求证:BD 是⊙O 的切线;
(2)求图中阴影部分的面积.
中考链接
解:(1)证明:连接OB,交CA于E,
∵∠C=30°,∠C= ∠BOA,∴∠BOA=60°.
∵∠BCA=∠OAC=30°,∴∠AEO=90°.
即OB⊥AC,
∵BD∥AC,∴∠DBE=∠AEO=90°.
∴BD是⊙O的切线;
(2)解:∵AC∥BD,∠OCA=90°,∴∠D=∠CAO=30°.
∵∠OBD=90°,OB=8,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
