【A典学案】冲刺100分 九年级上专题复习第七讲 直角三角形的边角关系 课件(共29张PPT)
文档属性
| 名称 | 【A典学案】冲刺100分 九年级上专题复习第七讲 直角三角形的边角关系 课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 11:31:24 | ||
图片预览







文档简介
第七讲 直角三角形的边角关系
北师大版 九年级上册
知识清单
1.锐角三角函数
△ABC 中,∠C=90°.∠A 的对边与邻边的比叫做∠A 的正切,记作 tan A,即 tan A=____________;
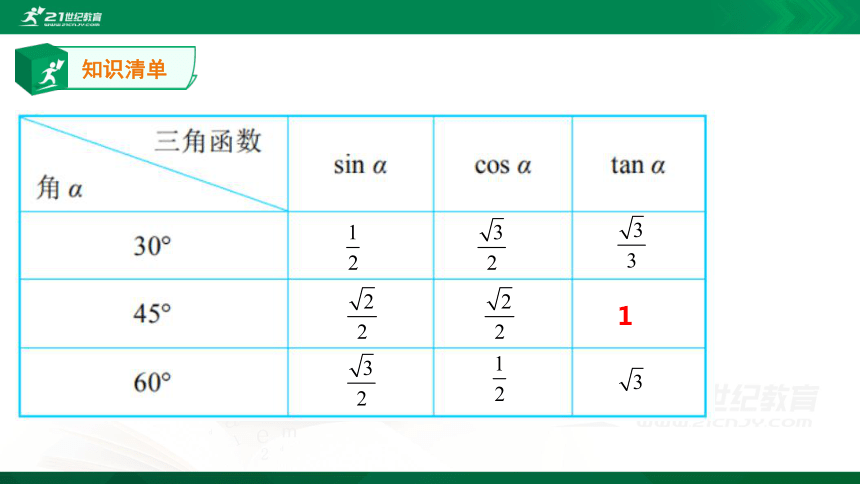
∠A 的对边与斜边的比叫做∠A 的正弦:记作 sin A,即 sin A=__________; ∠A 的邻边与斜边的比叫做∠A 的余弦:记作 cos A,即 cos A=_________; 2.30°,45°,60° 角的三角函数值
知识清单
1
知识清单
3.仰角和俯角
在视线与水平线所成的角中,视线在水平线上方的叫做________,视线在水平线下方的叫做________.
4.坡度和坡角
通常把坡面的垂直高度 h 和水平宽度 l 之比叫做________,用字母 i 表示,即 i=________.把坡面与水平面的夹角叫做________,记作∠α,于是 i=___=tan α,显然,坡度越大,α 角越大,坡面就越陡.
仰角
俯角
坡度
坡角
典例精讲
类型之一 锐角三角函数的有关计算
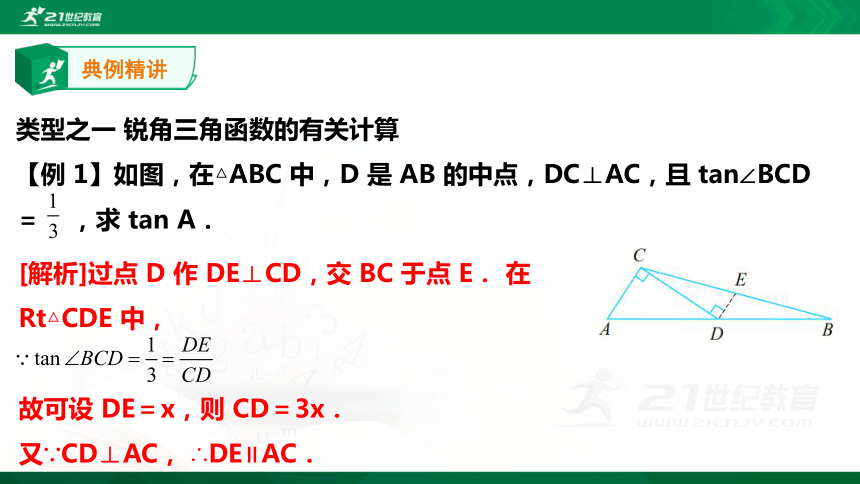
【例 1】如图,在△ABC 中,D 是 AB 的中点,DC⊥AC,且 tan∠BCD= ,求 tan A.
[解析]过点 D 作 DE⊥CD,交 BC 于点 E. 在 Rt△CDE 中,
故可设 DE=x,则 CD=3x.
又∵CD⊥AC, ∴DE∥AC.
典例精讲
又∵D 为 AB 的中点,
∴E 为 BC 的中点.
∴AC=2DE=2x. 在 Rt△ACD 中,∠ACD=90°,
AC=2x,CD=3x, ∴tan A= CD
变式训练
1.如图,在△ABC 中,AC=2, ,求 cos A 的值.
解:过点C作CD⊥AB于点D.
在Rt△BDC中,
又∵在Rt△ACD中,AC=2,
典例精讲
类型之二 特殊角的三角函数值
【例 2】计算:
[解析]原式=
变式训练
2.先化简,再求代数式 的值,其中 a=6 tan 60°-2
解:原式=
典例精讲
类型之三 解直角三角形
【例 3】如图,在△ABC 中,AD⊥BC 于点 D,AB=8,∠ABD=30°,∠CAD=45°,求 BC 的长.
[解析]∵AD⊥BC 于点 D,∴∠ADB=∠ADC=90°. 在 Rt△ABD 中,
∵AB=8,∠ABD=30°,
在 Rt△ADC 中,
∵∠CAD=45°,∠ADC=90°,
∴DC=AD=4.
变式训练
3.如图,在△ABC 中,已知 AC=2,∠B=30°,∠A=120°,求△ABC 的面积(结果可保留根号).
解:如图,过点C作CD⊥AB,与BA的延长线相交于点D.
∵AB=2,∠B=30°,∠CAB=120°,
∴∠CAD=60°,∠ACB=∠B=30°,∴AB=AC=2.
在Rt△ACD中,
典例精讲
类型之四 三角函数的应用
【例 4】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡 AE 的长度,她先在山脚下点 E 处测得山顶 A 的仰角是 30°,然后她沿着坡度是 i=1∶1(即 tan∠CED=1∶1)的斜坡步行 15 分钟到达 C 处,此时,测得 A 点的俯角是 15°.已知小丽的步行速度是18 米/分,图中点 A, B,E,D,C 在同一平面内,且点 D,E,B 在同一水平直线上.求出娱乐场地所在山坡 AE 的长度.(参考数据: ≈1.41,结果精确到 0.1 米)
典例精讲
[解析]过点 E 作 EF⊥AC 交 AC 于点 F. 在 Rt△CDE 中,
∵∠D=90°, ,∴∠CED=45°.
∵CK∥DB,∴∠KCE=∠CED=45°,
∴∠ECF=∠KCE-∠KCF=30°.
∵EF⊥AC,∴∠EFC=∠EFA=90°.
在 Rt△CFE 中,
又∵CE=18×15=270(米),∴EF=135 米.
∵∠CEF=90°-∠ECF=60°,∠AEB=30°,
典例精讲
∴∠AEF=180°-∠AEB-∠CEF-∠CED=45°,
∴在 Rt△AEF 中,EF=AE×cos ∠AEF= AE,
∴AE= 2 EF=135 ≈190.4(米).
答:娱乐场地所在山坡 AE 的长度约为 190.4 米.
变式训练
4.为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造,某试工单位为测得某河段的宽度,测量员先在河对岸岸边取一点 A,再在河这边沿河边取两点 B,C,在 B 处测得点 A 在北偏东 30°方向上,在点 C 处测得点 A 在西北方向上,量得 BC 长为 200米.
求小河的宽度(结果保留根号).
变式训练
解:过点A作AD⊥BC于点D.
根据题意,得∠ABC=90°-30°=60°,∠ACD=45°.∴∠CAD=45°,
∴∠ACD=∠CAD,∴AD=CD,∴BD=BC-CD=200-AD.
在Rt△ABD中,tan∠ABD= ,
∴AD=BD·tan∠ABD=(200-AD)·tan60°= (200-AD),
答:该河段的宽度为(300-100 )米.
区校真题
1.(龙岗)若锐角 A 满足 cos A= ,则∠A 的度数是( )
A.30° B.45° C.60° D.75°
2.(福田)如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点 C,测得∠BCA=37°,AC=28 米,∠BAC=45°,则这棵树的高 AB 约为( )(参考数据: )
A.14 米 B.15 米 C.17 米 D.18 米
A
C
区校真题
3.(宝安)如图,在 Rt△ABC 中,∠ABC=90°,BD⊥AC,垂足为点 D,如果 BC=4,sin∠DBC= ,那么线段 AB 的长是__________.
4.(福田)一个长方体木箱沿坡度 l=1∶ 坡面下滑,当木箱滑至如图位置时,AB=3 m,已知木箱高BE= m,则木箱端点 E 距地面 AC 的高度 EF 为_____________m.
3
区校真题
5.(罗湖)为庆祝中华人民共和国成立 70 周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB 的高度,他们在地面 C 处测得另一幢大厦 DE 的顶部 E 处的仰角为 32°,测得“平安中心”AB的顶部 A 处的仰角为 44°.登上大厦 DE 的顶部 E 处后,测得“平安中心”AB 的顶部 A 处的仰角为 60°(如图所示).已知 C,D,B 三点在同一水平直线上,且 CD=400 米,求平安金融中心 AB 的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,tan44°≈0.99, )
区校真题
解:过点E作EF∥BC交AB于点F,如图所示:
∵DE=CD·tan 32°=400×tan 32°,
设BD=x,则AB=BC·tan 44°=(400+x)tan 44°,
∴AF=AB-BF=AB-DE=(400+x)tan 44°-400×tan 32°.
∴ =tan 60°,分别把AF,BF代入上式可得出x值,即x=200.
把x值代入AB=BC·tan 44°=(400+x)tan 44°中,得AB=600×tan 44°=594.
故平安金融中心AB的高度为594 m.
区校真题
6.(2020 龙华二模,20)在“停课不停学”期间,小明用电脑在线上课,图 1 是他的电脑液晶显示器的侧面图,显示屏 AB 可以绕 O 点旋转一定角度.研究表明:当眼睛 E 与显示屏顶端 A 在同一水平线上,且望向显示器屏幕形成一个 18°俯角(即望向屏幕中心 P 的的视线 EP 与水平线 EA 的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端 A 与底座 C 的连线 AC 与水平线 CD 垂直时(如图 2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽 AB 为 32 cm.
(1)求眼睛 E 与显示屏顶端 A 的水平距离 AE;(结果精确到 1 cm)
区校真题
(2)求显示屏顶端 A 与底座 C 的距离 AC.(结果精确到 1 cm)
(参考数据:sin18°≈0.3,cos18°≈0.9, )
区校真题
解:(1)由已知得AP=BP= AB=16 cm,
在Rt△APE中, ,
答:眼睛E与显示屏顶端A的水平距离AE约为53 cm.
(2)如图,过点B作BF⊥AC于点F.
∵∠EAB+∠BAF=90°,∠EAB+∠AEP=90°,∴∠BAF=∠AEP=18°.
在Rt△ABF中,AF=AB·cos∠BAF=32×cos 18°≈32×0.9≈28.8,
BF=AB·sin∠BAF=32×sin 18°≈32×0.3≈9.6.
∵BF∥CD,∴∠CBF=∠BCD=30°.
区校真题
∴AC=AF+CF=28.8+5.44≈34(cm).
答:显示屏顶端A与底座C的距离AC约为34 cm.
中考链接
1.如图,在△ABC 中,AD 是 BC 边上的高,AE 是 BC 边上的中线,∠C=45°,sin B= ,AD=1. (1)求 BC 的长;
(2)求 tan∠DAE 的值.
解:(1)∵AB是BC边上的高,∴AD⊥BC.
在Rt△ABD中,∵sin B=
又∵AD=1,∴AB=3,∴BD=
在Rt△ADC中,∵∠C=45°,∴CD=AD=1,∴BC= +1.
(2)∵AE是BC边上的中线,
中考链接
2.如图,一艘海轮位于灯塔 P 的北偏东 65°方向,距离灯塔 80 海里的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 45°方向上的 B 处,这时,海轮所在的 B 处距离灯塔 P 有多远?(结果用非特殊角的三角函数及根式表示即可)
中考链接
解:如图,过点P作PD⊥AB于点D.
由题意知∠DPB=∠DBP=45°.
在Rt△PBD中, ,∴PB= PD.
∵点A在点P的北偏东65°方向上,∴∠APD=90°-65°=25°.
在Rt△PAD中,cos25°= .
∴PD=PAcos25°=80cos25°(海里),∴PB=80 cos25°(海里).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版 九年级上册
知识清单
1.锐角三角函数
△ABC 中,∠C=90°.∠A 的对边与邻边的比叫做∠A 的正切,记作 tan A,即 tan A=____________;
∠A 的对边与斜边的比叫做∠A 的正弦:记作 sin A,即 sin A=__________; ∠A 的邻边与斜边的比叫做∠A 的余弦:记作 cos A,即 cos A=_________; 2.30°,45°,60° 角的三角函数值
知识清单
1
知识清单
3.仰角和俯角
在视线与水平线所成的角中,视线在水平线上方的叫做________,视线在水平线下方的叫做________.
4.坡度和坡角
通常把坡面的垂直高度 h 和水平宽度 l 之比叫做________,用字母 i 表示,即 i=________.把坡面与水平面的夹角叫做________,记作∠α,于是 i=___=tan α,显然,坡度越大,α 角越大,坡面就越陡.
仰角
俯角
坡度
坡角
典例精讲
类型之一 锐角三角函数的有关计算
【例 1】如图,在△ABC 中,D 是 AB 的中点,DC⊥AC,且 tan∠BCD= ,求 tan A.
[解析]过点 D 作 DE⊥CD,交 BC 于点 E. 在 Rt△CDE 中,
故可设 DE=x,则 CD=3x.
又∵CD⊥AC, ∴DE∥AC.
典例精讲
又∵D 为 AB 的中点,
∴E 为 BC 的中点.
∴AC=2DE=2x. 在 Rt△ACD 中,∠ACD=90°,
AC=2x,CD=3x, ∴tan A= CD
变式训练
1.如图,在△ABC 中,AC=2, ,求 cos A 的值.
解:过点C作CD⊥AB于点D.
在Rt△BDC中,
又∵在Rt△ACD中,AC=2,
典例精讲
类型之二 特殊角的三角函数值
【例 2】计算:
[解析]原式=
变式训练
2.先化简,再求代数式 的值,其中 a=6 tan 60°-2
解:原式=
典例精讲
类型之三 解直角三角形
【例 3】如图,在△ABC 中,AD⊥BC 于点 D,AB=8,∠ABD=30°,∠CAD=45°,求 BC 的长.
[解析]∵AD⊥BC 于点 D,∴∠ADB=∠ADC=90°. 在 Rt△ABD 中,
∵AB=8,∠ABD=30°,
在 Rt△ADC 中,
∵∠CAD=45°,∠ADC=90°,
∴DC=AD=4.
变式训练
3.如图,在△ABC 中,已知 AC=2,∠B=30°,∠A=120°,求△ABC 的面积(结果可保留根号).
解:如图,过点C作CD⊥AB,与BA的延长线相交于点D.
∵AB=2,∠B=30°,∠CAB=120°,
∴∠CAD=60°,∠ACB=∠B=30°,∴AB=AC=2.
在Rt△ACD中,
典例精讲
类型之四 三角函数的应用
【例 4】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡 AE 的长度,她先在山脚下点 E 处测得山顶 A 的仰角是 30°,然后她沿着坡度是 i=1∶1(即 tan∠CED=1∶1)的斜坡步行 15 分钟到达 C 处,此时,测得 A 点的俯角是 15°.已知小丽的步行速度是18 米/分,图中点 A, B,E,D,C 在同一平面内,且点 D,E,B 在同一水平直线上.求出娱乐场地所在山坡 AE 的长度.(参考数据: ≈1.41,结果精确到 0.1 米)
典例精讲
[解析]过点 E 作 EF⊥AC 交 AC 于点 F. 在 Rt△CDE 中,
∵∠D=90°, ,∴∠CED=45°.
∵CK∥DB,∴∠KCE=∠CED=45°,
∴∠ECF=∠KCE-∠KCF=30°.
∵EF⊥AC,∴∠EFC=∠EFA=90°.
在 Rt△CFE 中,
又∵CE=18×15=270(米),∴EF=135 米.
∵∠CEF=90°-∠ECF=60°,∠AEB=30°,
典例精讲
∴∠AEF=180°-∠AEB-∠CEF-∠CED=45°,
∴在 Rt△AEF 中,EF=AE×cos ∠AEF= AE,
∴AE= 2 EF=135 ≈190.4(米).
答:娱乐场地所在山坡 AE 的长度约为 190.4 米.
变式训练
4.为建设“宜居宜业宜游”山水园林式城市,内江市正在对城区沱江河段进行区域性景观打造,某试工单位为测得某河段的宽度,测量员先在河对岸岸边取一点 A,再在河这边沿河边取两点 B,C,在 B 处测得点 A 在北偏东 30°方向上,在点 C 处测得点 A 在西北方向上,量得 BC 长为 200米.
求小河的宽度(结果保留根号).
变式训练
解:过点A作AD⊥BC于点D.
根据题意,得∠ABC=90°-30°=60°,∠ACD=45°.∴∠CAD=45°,
∴∠ACD=∠CAD,∴AD=CD,∴BD=BC-CD=200-AD.
在Rt△ABD中,tan∠ABD= ,
∴AD=BD·tan∠ABD=(200-AD)·tan60°= (200-AD),
答:该河段的宽度为(300-100 )米.
区校真题
1.(龙岗)若锐角 A 满足 cos A= ,则∠A 的度数是( )
A.30° B.45° C.60° D.75°
2.(福田)如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点 C,测得∠BCA=37°,AC=28 米,∠BAC=45°,则这棵树的高 AB 约为( )(参考数据: )
A.14 米 B.15 米 C.17 米 D.18 米
A
C
区校真题
3.(宝安)如图,在 Rt△ABC 中,∠ABC=90°,BD⊥AC,垂足为点 D,如果 BC=4,sin∠DBC= ,那么线段 AB 的长是__________.
4.(福田)一个长方体木箱沿坡度 l=1∶ 坡面下滑,当木箱滑至如图位置时,AB=3 m,已知木箱高BE= m,则木箱端点 E 距地面 AC 的高度 EF 为_____________m.
3
区校真题
5.(罗湖)为庆祝中华人民共和国成立 70 周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB 的高度,他们在地面 C 处测得另一幢大厦 DE 的顶部 E 处的仰角为 32°,测得“平安中心”AB的顶部 A 处的仰角为 44°.登上大厦 DE 的顶部 E 处后,测得“平安中心”AB 的顶部 A 处的仰角为 60°(如图所示).已知 C,D,B 三点在同一水平直线上,且 CD=400 米,求平安金融中心 AB 的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,tan44°≈0.99, )
区校真题
解:过点E作EF∥BC交AB于点F,如图所示:
∵DE=CD·tan 32°=400×tan 32°,
设BD=x,则AB=BC·tan 44°=(400+x)tan 44°,
∴AF=AB-BF=AB-DE=(400+x)tan 44°-400×tan 32°.
∴ =tan 60°,分别把AF,BF代入上式可得出x值,即x=200.
把x值代入AB=BC·tan 44°=(400+x)tan 44°中,得AB=600×tan 44°=594.
故平安金融中心AB的高度为594 m.
区校真题
6.(2020 龙华二模,20)在“停课不停学”期间,小明用电脑在线上课,图 1 是他的电脑液晶显示器的侧面图,显示屏 AB 可以绕 O 点旋转一定角度.研究表明:当眼睛 E 与显示屏顶端 A 在同一水平线上,且望向显示器屏幕形成一个 18°俯角(即望向屏幕中心 P 的的视线 EP 与水平线 EA 的夹角∠AEP)时,对保护眼睛比较好,而且显示屏顶端 A 与底座 C 的连线 AC 与水平线 CD 垂直时(如图 2)时,观看屏幕最舒适,此时测得∠BCD=30°,∠APE=90°,液晶显示屏的宽 AB 为 32 cm.
(1)求眼睛 E 与显示屏顶端 A 的水平距离 AE;(结果精确到 1 cm)
区校真题
(2)求显示屏顶端 A 与底座 C 的距离 AC.(结果精确到 1 cm)
(参考数据:sin18°≈0.3,cos18°≈0.9, )
区校真题
解:(1)由已知得AP=BP= AB=16 cm,
在Rt△APE中, ,
答:眼睛E与显示屏顶端A的水平距离AE约为53 cm.
(2)如图,过点B作BF⊥AC于点F.
∵∠EAB+∠BAF=90°,∠EAB+∠AEP=90°,∴∠BAF=∠AEP=18°.
在Rt△ABF中,AF=AB·cos∠BAF=32×cos 18°≈32×0.9≈28.8,
BF=AB·sin∠BAF=32×sin 18°≈32×0.3≈9.6.
∵BF∥CD,∴∠CBF=∠BCD=30°.
区校真题
∴AC=AF+CF=28.8+5.44≈34(cm).
答:显示屏顶端A与底座C的距离AC约为34 cm.
中考链接
1.如图,在△ABC 中,AD 是 BC 边上的高,AE 是 BC 边上的中线,∠C=45°,sin B= ,AD=1. (1)求 BC 的长;
(2)求 tan∠DAE 的值.
解:(1)∵AB是BC边上的高,∴AD⊥BC.
在Rt△ABD中,∵sin B=
又∵AD=1,∴AB=3,∴BD=
在Rt△ADC中,∵∠C=45°,∴CD=AD=1,∴BC= +1.
(2)∵AE是BC边上的中线,
中考链接
2.如图,一艘海轮位于灯塔 P 的北偏东 65°方向,距离灯塔 80 海里的 A 处,它沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 45°方向上的 B 处,这时,海轮所在的 B 处距离灯塔 P 有多远?(结果用非特殊角的三角函数及根式表示即可)
中考链接
解:如图,过点P作PD⊥AB于点D.
由题意知∠DPB=∠DBP=45°.
在Rt△PBD中, ,∴PB= PD.
∵点A在点P的北偏东65°方向上,∴∠APD=90°-65°=25°.
在Rt△PAD中,cos25°= .
∴PD=PAcos25°=80cos25°(海里),∴PB=80 cos25°(海里).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
